So führen sie eine zweifaktorielle anova in spss durch
Eine zweifaktorielle ANOVA wird verwendet, um zu bestimmen, ob ein statistisch signifikanter Unterschied zwischen den Mittelwerten von drei oder mehr unabhängigen Gruppen besteht, die auf zwei Faktoren aufgeteilt wurden.
Der Zweck einer zweifaktoriellen ANOVA besteht darin, den Einfluss zweier Faktoren auf eine Antwortvariable zu bestimmen und festzustellen, ob eine Wechselwirkung zwischen den beiden Faktoren auf die Antwortvariable besteht oder nicht.
In diesem Tutorial wird erläutert, wie Sie eine zweifaktorielle ANOVA in SPSS durchführen.
Beispiel: Zweifaktorielle ANOVA in SPSS
Ein Botaniker möchte wissen, ob das Pflanzenwachstum durch die Sonneneinstrahlung und die Häufigkeit des Gießens beeinflusst wird. Sie pflanzt 30 Samen und lässt sie zwei Monate lang unter unterschiedlichen Bedingungen der Sonneneinstrahlung und Bewässerungshäufigkeit wachsen. Nach zwei Monaten zeichnet sie die Höhe jeder Pflanze in Zoll auf.
Die Ergebnisse sind unten dargestellt:
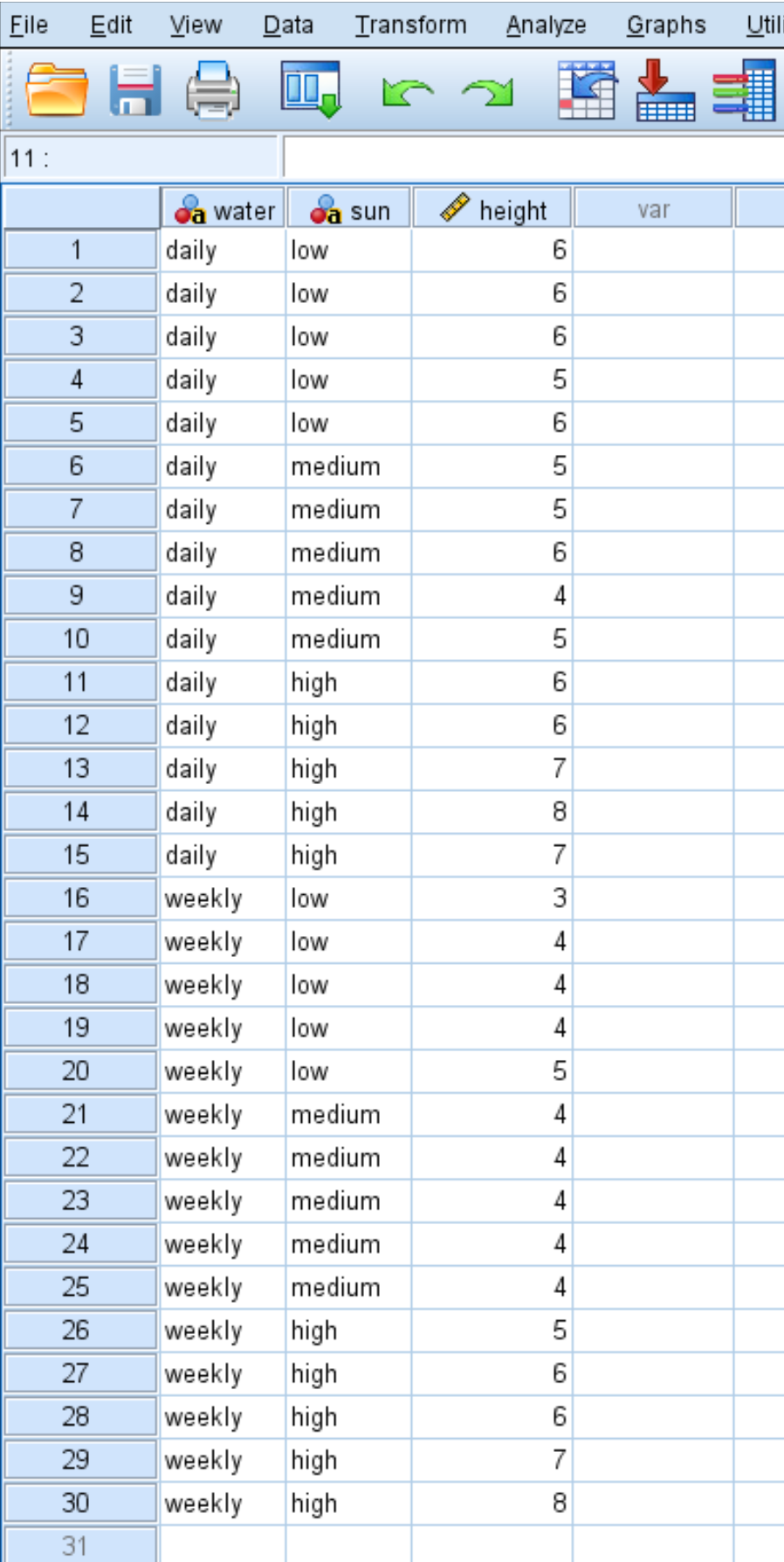
Verwenden Sie die folgenden Schritte, um eine zweifaktorielle ANOVA durchzuführen, um zu bestimmen, ob Bewässerungshäufigkeit und Sonneneinstrahlung einen signifikanten Einfluss auf das Pflanzenwachstum haben, und um festzustellen, ob es einen Wechselwirkungseffekt zwischen Wasserhäufigkeit und Sonneneinstrahlung gibt. Bewässerung und Sonneneinstrahlung.
Schritt 1: Führen Sie die zweifaktorielle ANOVA durch.
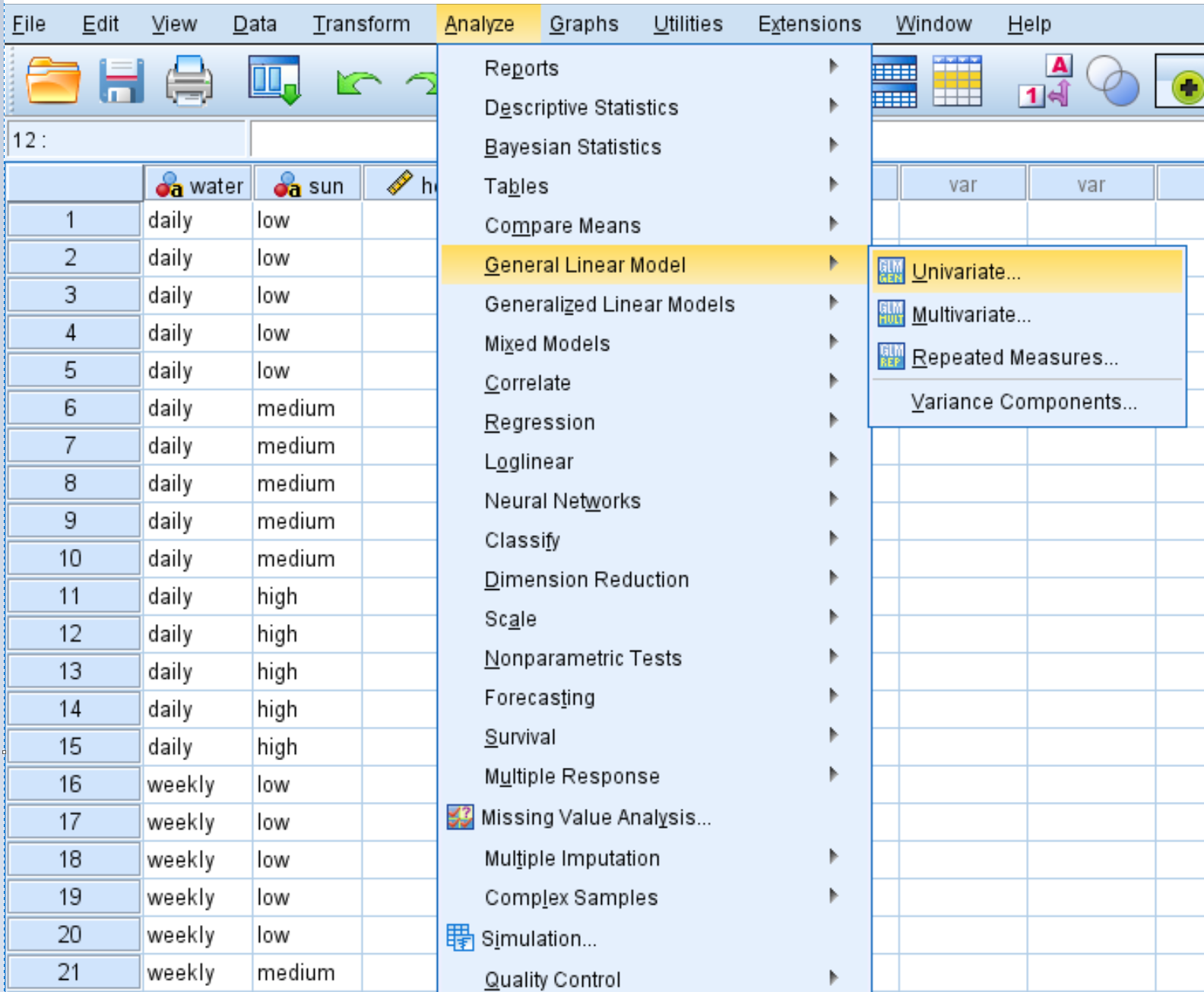
Klicken Sie auf die Registerkarte „Analysieren“ , dann auf „Allgemeines lineares Modell“ und dann auf „Univariate“ :
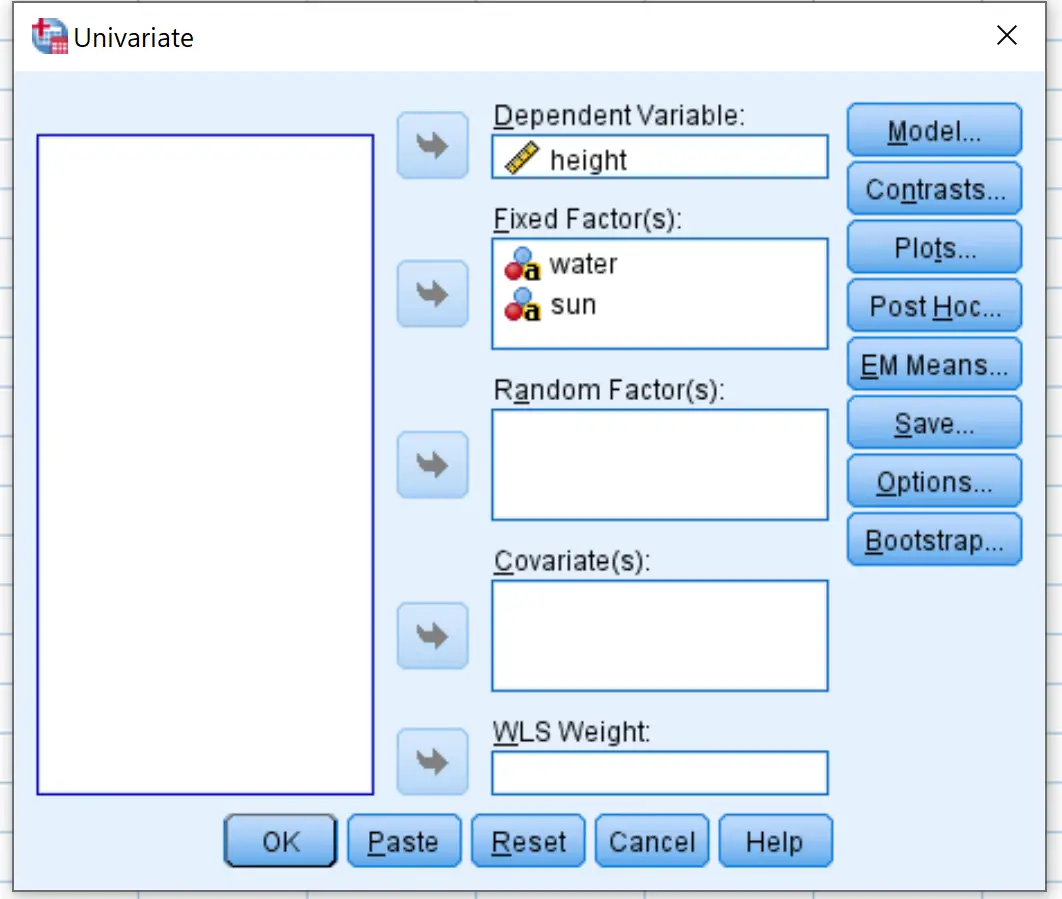
Ziehen Sie die Höhe der Antwortvariablen in das Feld mit der Bezeichnung „Abhängige Variable“. Ziehen Sie die beiden Wasser- und Sonnenfaktorvariablen in das Feld mit der Bezeichnung „Fester Faktor“:
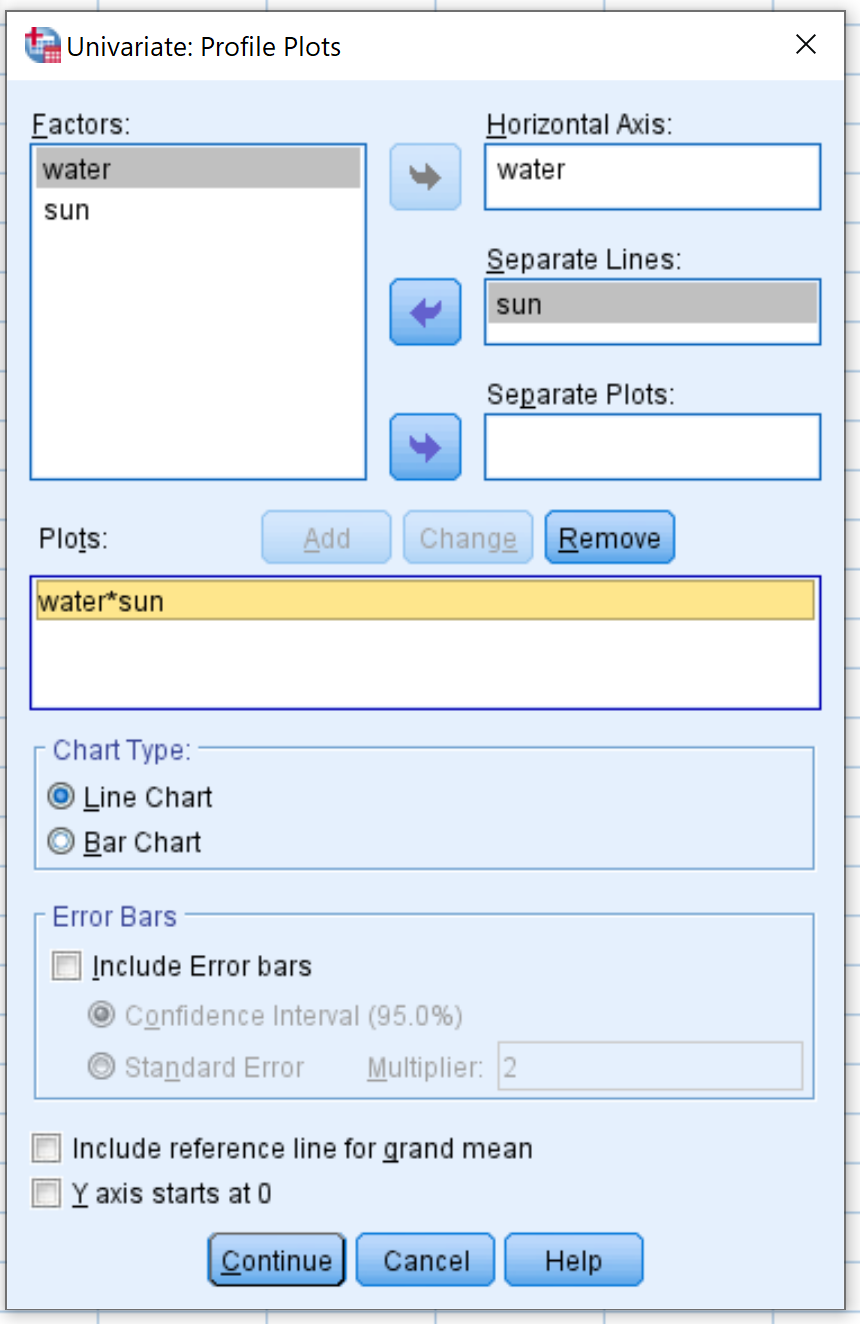
Klicken Sie anschließend auf die Schaltfläche Diagramme . Ziehen Sie das Wasser in den Bereich mit der Bezeichnung „Horizontale Achse“ und die Sonne in den Bereich mit der Bezeichnung „Getrennte Linien“. Klicken Sie dann auf Hinzufügen . Die Wörter „Wasser*Sonne“ werden im Feld „Plots“ angezeigt. Klicken Sie dann auf Weiter .
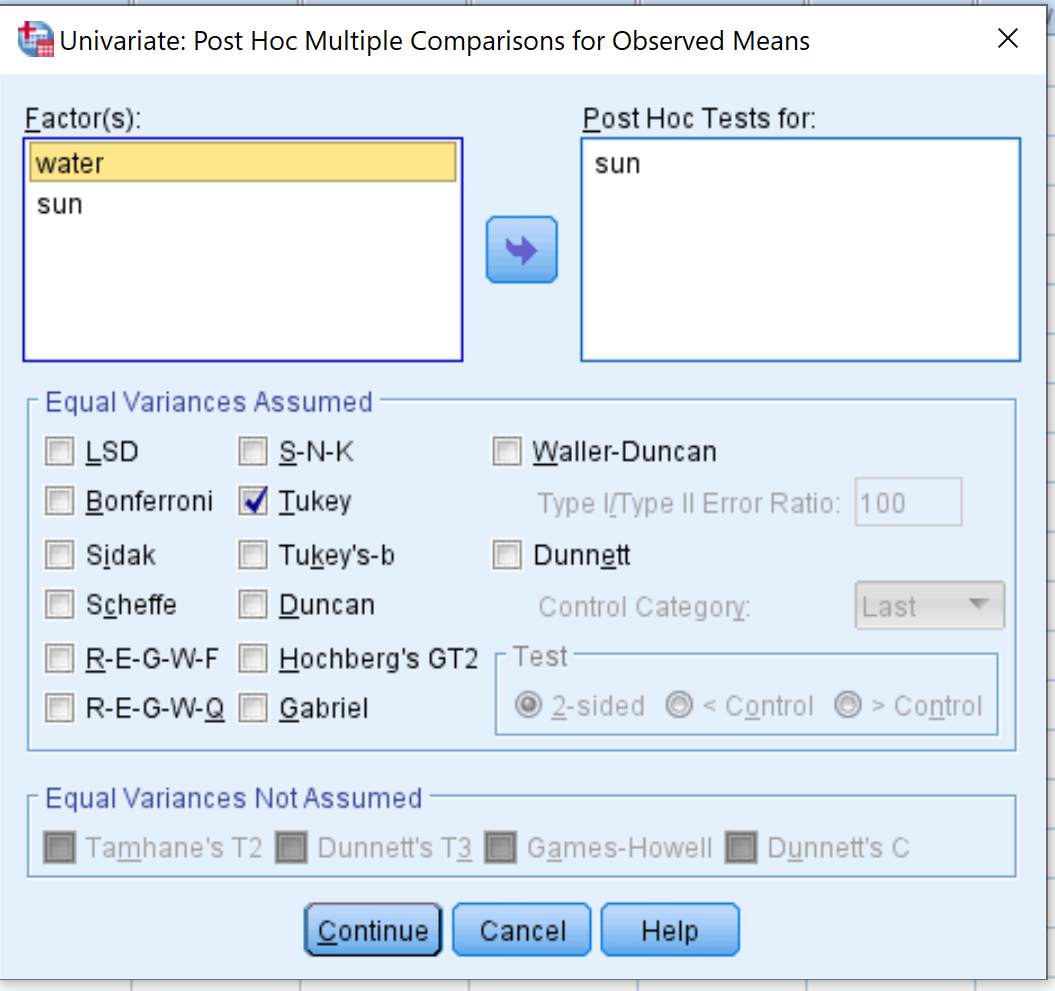
Klicken Sie anschließend auf die Schaltfläche „Post Hoc“ . Ziehen Sie im neuen Fenster, das erscheint, die Sonnenvariable in das Feld mit der Bezeichnung „Post-Hoc-Tests für“. Aktivieren Sie dann das Kontrollkästchen neben Tukey . Klicken Sie dann auf Weiter .
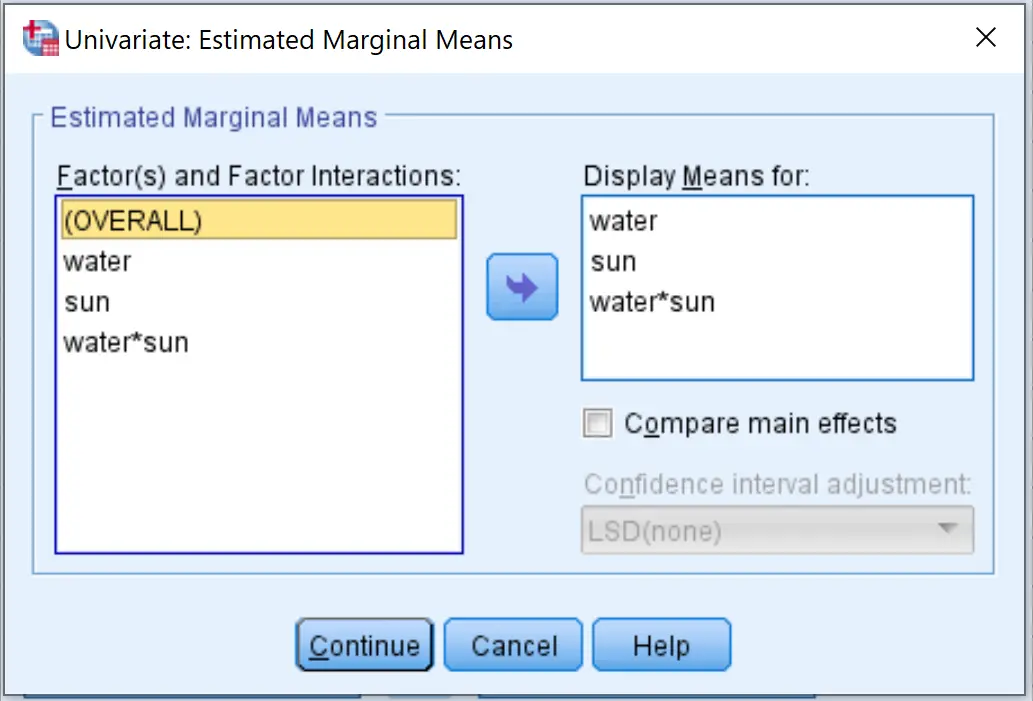
Klicken Sie anschließend auf die Schaltfläche EM Means . Ziehen Sie die folgenden Variablen in das Feld mit der Bezeichnung „Durchschnitte anzeigen für“. Klicken Sie dann auf Weiter .
Klicken Sie abschließend auf OK .
Schritt 2: Interpretieren Sie die Ergebnisse.
Sobald Sie auf „OK“ klicken, werden die Ergebnisse der Zwei-Wege-ANOVA angezeigt. So interpretieren Sie die Ergebnisse:
Tests von Zwischensubjekteffekten
Die erste Tabelle zeigt die p-Werte für die Faktoren Wasser und Sonne sowie den Wechselwirkungseffekt Wasser*Sonne :
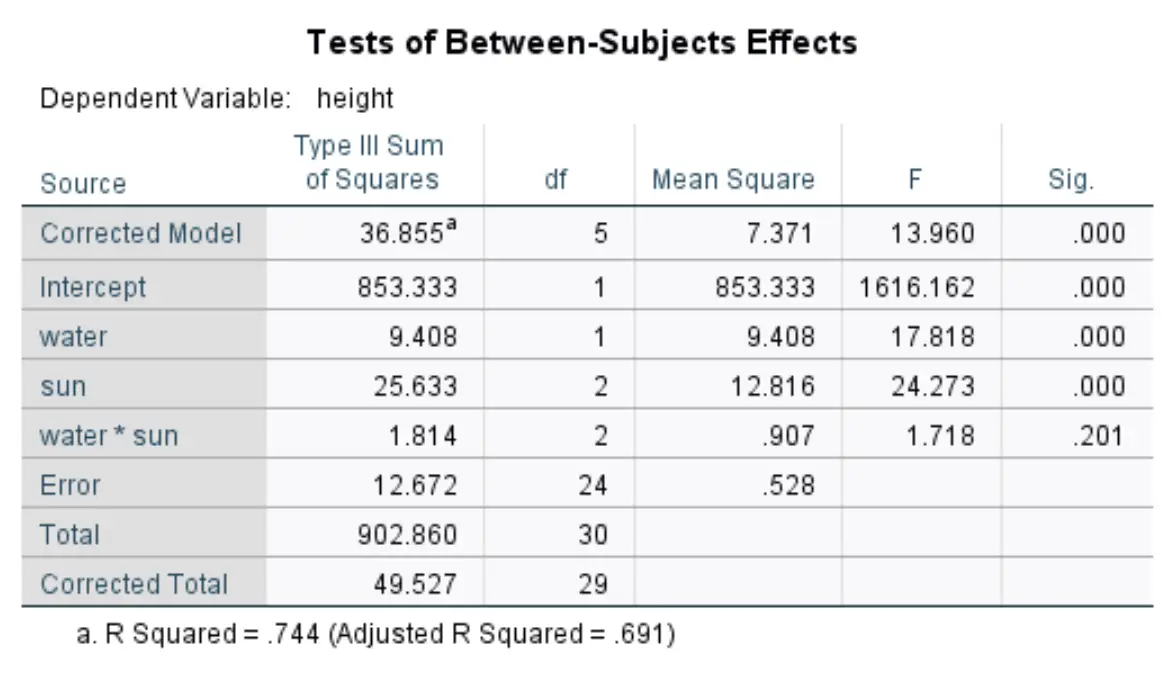
Wir können die folgenden p-Werte für jeden der Faktoren in der Tabelle sehen:
- Wasser: p-Wert = 0,000
- Sonne: p-Wert = 0,000
- Wasser*Sonne: p-Wert = 0,201
Da der p-Wert für Wasser und Sonne unter 0,05 liegt, bedeutet dies, dass beide Faktoren einen statistisch signifikanten Einfluss auf die Pflanzenhöhe haben.
Und da der p-Wert für den Wechselwirkungseffekt (0,201) nicht weniger als 0,05 beträgt, bedeutet dies, dass es keinen signifikanten Wechselwirkungseffekt zwischen Sonneneinstrahlung und der Bewässerungshäufigkeit gibt.
Geschätzte Grenzmittelwerte
Die erste Tabelle zeigt die Durchschnittswerte der Beobachtungen für jeden Faktor:
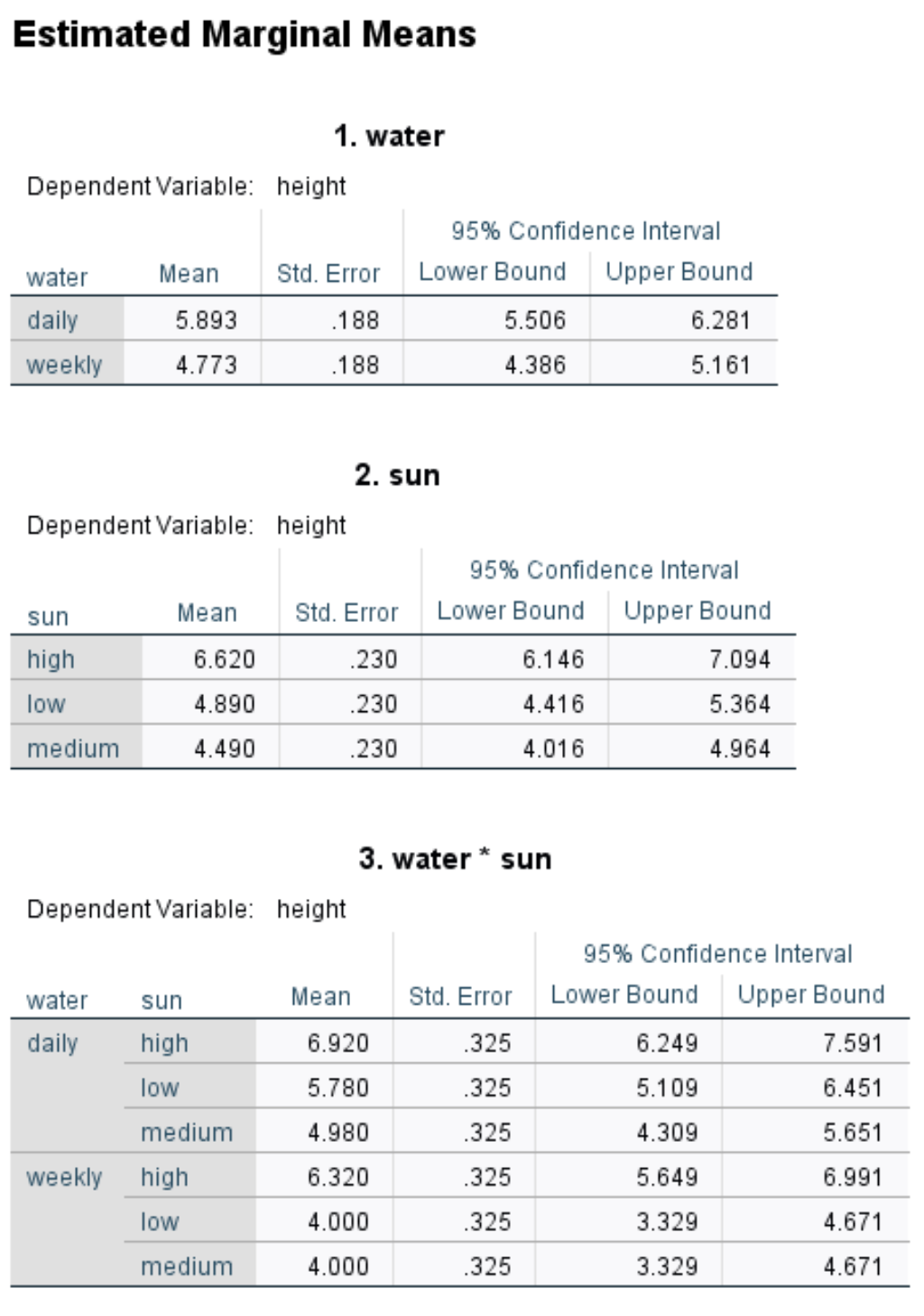
Zum Beispiel:
- Die durchschnittliche Höhe der täglich bewässerten Pflanzen betrug 5,893 Zoll.
- Die durchschnittliche Höhe der Pflanzen bei starker Sonneneinstrahlung betrug 6,62 Zoll.
- Die durchschnittliche Höhe der täglich bewässerten und stark dem Sonnenlicht ausgesetzten Pflanzen betrug 6,32 Zoll.
Und so weiter.
Post-hoc-Tests
Diese Tabelle zeigt p-Werte für Tukeys Post-hoc-Vergleiche zwischen den drei verschiedenen Sonnenexpositionsgraden.
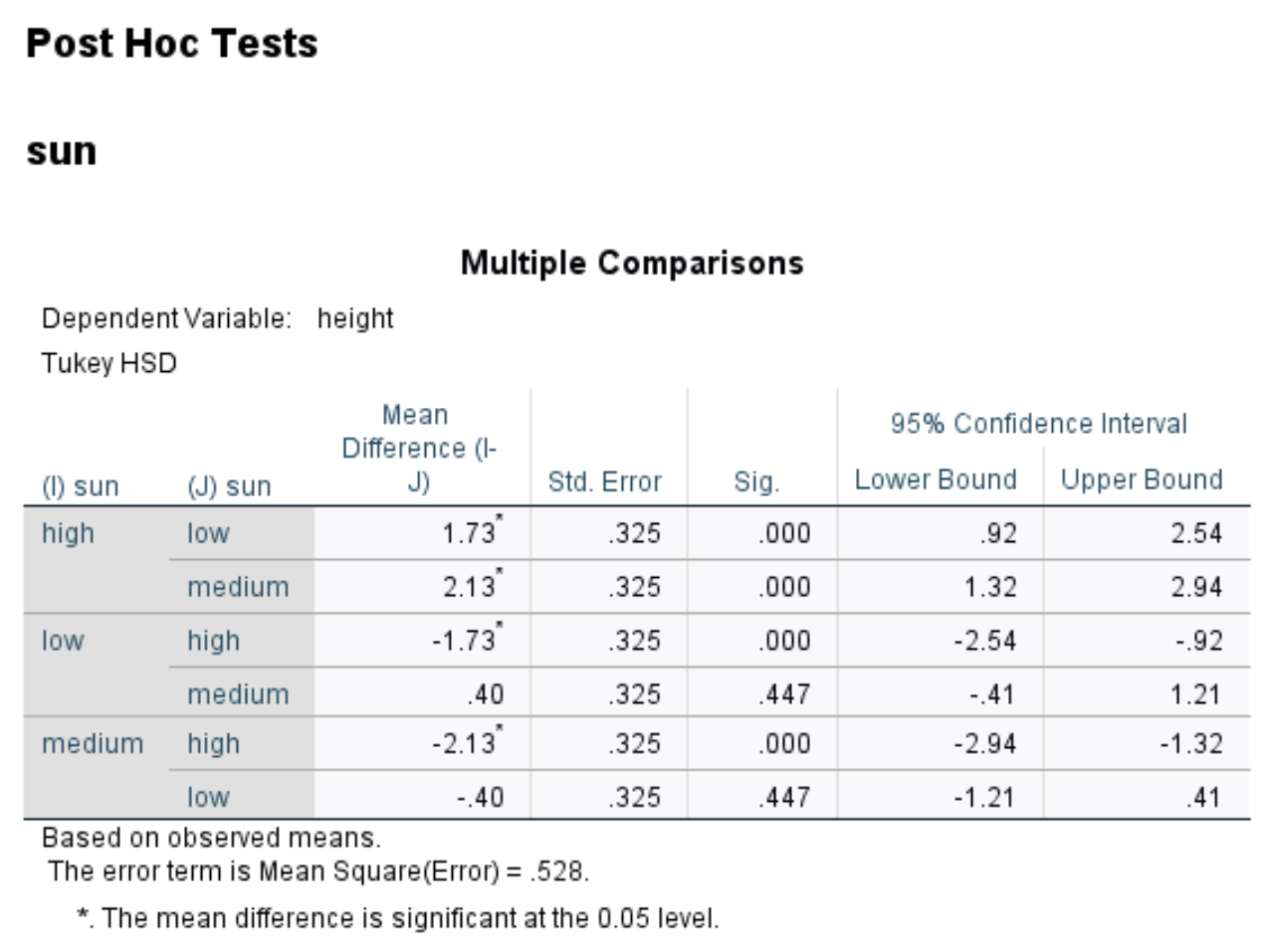
In der Tabelle sehen wir die p-Werte für die folgenden Vergleiche:
- hoch vs. niedrig: | p-Wert = 0,000
- hoch vs. mittel | p-Wert = 0,000
- niedrig vs. mittel | p-Wert = 0,447
Dies zeigt uns, dass es einen statistisch signifikanten Unterschied zwischen hoher und niedriger Sonneneinstrahlung sowie hoher und mittlerer Sonneneinstrahlung gibt, aber keinen signifikanten Unterschied zwischen niedriger und mittlerer Sonneneinstrahlung.
Schritt 3: Melden Sie die Ergebnisse.
Schließlich können wir über die Ergebnisse der zweifaktoriellen ANOVA berichten. Hier ist ein Beispiel dafür:
Eine Zwei-Wege-ANOVA wurde durchgeführt, um zu bestimmen, ob die Bewässerungshäufigkeit (täglich oder wöchentlich) und die Sonneneinstrahlung (niedrig, mittel, hoch) einen signifikanten Einfluss auf das Pflanzenwachstum hatten. Insgesamt wurden 30 Pflanzen in der Studie verwendet.
Eine Zwei-Wege-ANOVA ergab, dass sowohl die Bewässerungshäufigkeit (p < 0,000) als auch die Sonneneinstrahlung (p < 0,000) einen statistisch signifikanten Einfluss auf das Pflanzenwachstum hatten.
Pflanzen, die täglich gegossen wurden, verzeichneten ein deutlich höheres Wachstum als Pflanzen, die wöchentlich gegossen wurden.
Darüber hinaus ergab Tukeys Test für mehrere Vergleiche, dass Pflanzen, die einer hohen Sonneneinstrahlung ausgesetzt waren, ein deutlich höheres Wachstum aufwiesen als Pflanzen, die einer mittleren oder geringen Sonneneinstrahlung ausgesetzt waren. Es gab jedoch keinen signifikanten Unterschied zwischen Pflanzen, die mittlerer und geringer Sonneneinstrahlung ausgesetzt waren.
Es gab auch keinen statistisch signifikanten Wechselwirkungseffekt zwischen Bewässerungshäufigkeit und Sonneneinstrahlung.