अनुमान और भविष्यवाणी: क्या अंतर है?

अक्सर सांख्यिकी में हम डेटा का उपयोग दो कारणों में से एक के लिए करना चाहते हैं:

(1) अनुमान: हम मौजूदा डेटासेट में भविष्यवक्ता चर और प्रतिक्रिया चर के बीच संबंध की प्रकृति को समझना चाहते हैं।

(2) भविष्यवाणी: हम एक मॉडल बनाने के लिए मौजूदा डेटासेट का उपयोग करना चाहते हैं जो एक नए अवलोकन के प्रतिक्रिया चर के मूल्य की भविष्यवाणी करता है।

उदाहरण के लिए, मान लीजिए कि हमारे पास निम्नलिखित डेटासेट हैं जिनमें घरों के बारे में जानकारी है:

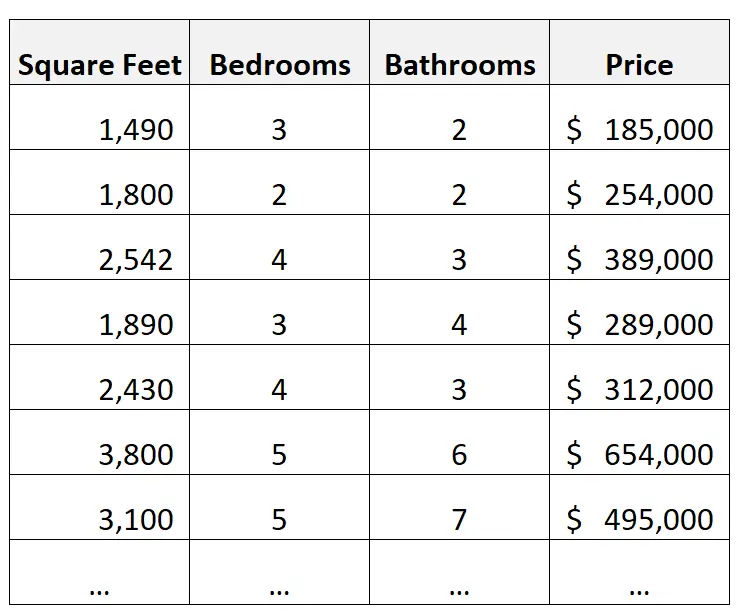
अनुमान का एक उदाहरण:

मान लीजिए कि हम भविष्यवक्ता चर के रूप में वर्ग फुटेज, शयनकक्षों की संख्या और बाथरूमों की संख्या और प्रतिक्रिया चर के रूप में कीमत का उपयोग करके एक बहु रेखीय प्रतिगमन मॉडल बनाते हैं।

फिर हम प्रत्येक भविष्यवक्ता चर में एक-इकाई परिवर्तन से जुड़े मूल्य में औसत परिवर्तन को समझने के लिए प्रतिगमन गुणांक का उपयोग कर सकते हैं।

उदाहरण के लिए, हम समझ सकते हैं कि प्रत्येक अतिरिक्त शयनकक्ष, प्रत्येक अतिरिक्त बाथरूम और प्रत्येक अतिरिक्त वर्ग फुट के साथ कीमत में (औसतन) कितना परिवर्तन होता है।

भविष्यवाणी का एक उदाहरण:

हम एक ही मल्टीपल लीनियर रिग्रेशन मॉडल बना सकते हैं और इसका उपयोग एक नए घर के वर्ग फुटेज, शयनकक्षों की संख्या और बाथरूमों की संख्या के आधार पर उसके मूल्य की भविष्यवाणी करने के लिए कर सकते हैं।

उदाहरण के लिए, हम 3 शयनकक्षों, 3 स्नानघरों और 2,000 वर्ग फुट वाले नए घर की कीमत का अनुमान लगाने के लिए मॉडल का उपयोग कर सकते हैं।

फिर हम अपनी भविष्यवाणी की तुलना वास्तविक लिस्टिंग मूल्य से कर सकते हैं और आकलन कर सकते हैं कि घर का मूल्य कम या अधिक है या नहीं।

निम्नलिखित उदाहरण विभिन्न परिदृश्यों में अनुमान और भविष्यवाणी के बीच अंतर को दर्शाते हैं:

उदाहरण 1: खेल में अनुमान और भविष्यवाणी

मान लीजिए कि हमारे पास निम्नलिखित डेटासेट है जिसमें पेशेवर बास्केटबॉल टीमों के बारे में जानकारी है:

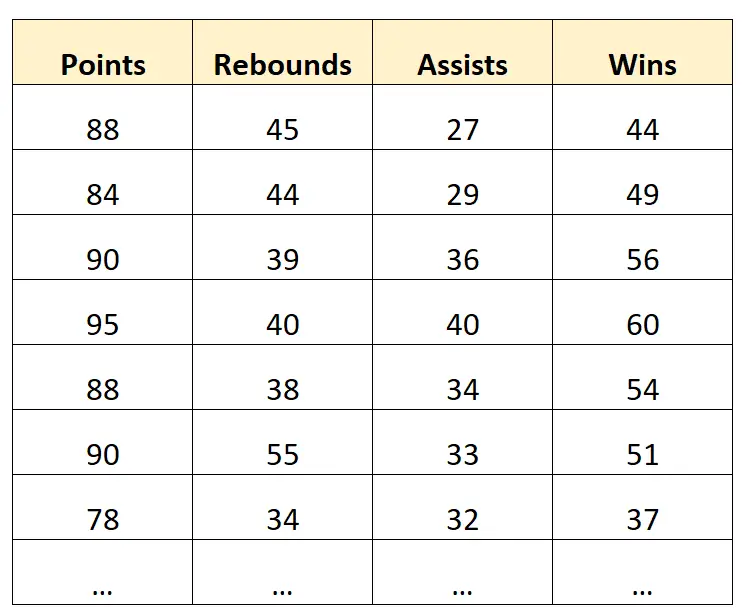
अनुमान का एक उदाहरण:

मान लीजिए कि हम अंक, रिबाउंड और सहायता को भविष्यवक्ता चर के रूप में और जीत को प्रतिक्रिया चर के रूप में उपयोग करके एक बहु रेखीय प्रतिगमन मॉडल बनाते हैं।

फिर हम यह समझने के लिए मॉडल का उपयोग कर सकते हैं कि प्रत्येक अतिरिक्त अंक, रिबाउंड और सहायता के साथ जीत की संख्या (औसतन) कितनी बदलती है।

भविष्यवाणी का एक उदाहरण:

हम समान मल्टीपल लीनियर रिग्रेशन मॉडल का निर्माण कर सकते हैं और इसका उपयोग यह अनुमान लगाने के लिए कर सकते हैं कि एक टीम अपने अंकों, रिबाउंड और सहायता के आधार पर कितनी जीत हासिल करेगी।

उदाहरण के लिए, हम मॉडल का उपयोग यह अनुमान लगाने के लिए कर सकते हैं कि 90 अंक, 40 रिबाउंड और 30 सहायता वाली टीम कितनी जीत हासिल करेगी।

उदाहरण 2: व्यवसाय में अनुमान और भविष्यवाणी

मान लीजिए कि हमारे पास निम्नलिखित डेटासेट हैं जिनमें विभिन्न कंपनियों के वार्षिक राजस्व (लाखों में) की जानकारी है:

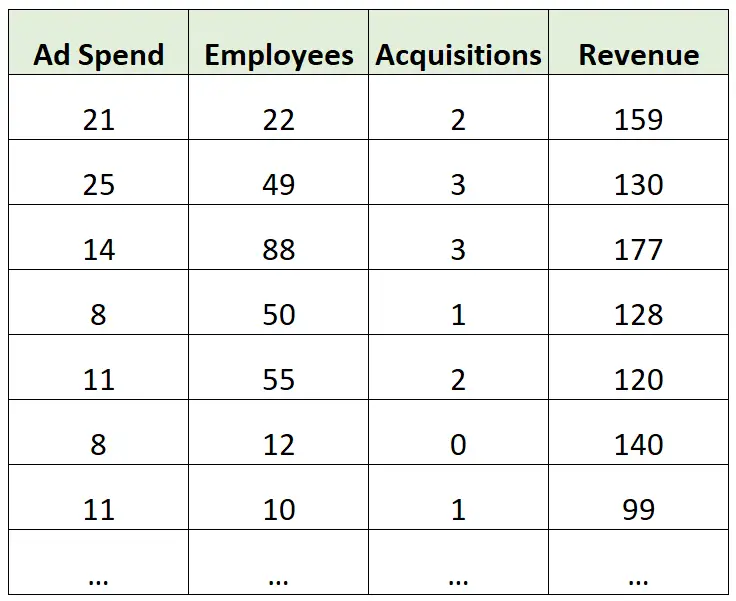
अनुमान का एक उदाहरण:

मान लीजिए कि हम विज्ञापन खर्च, कर्मचारियों की संख्या और कुल अधिग्रहणों को पूर्वानुमानक चर के रूप में और वार्षिक राजस्व को प्रतिक्रिया चर के रूप में उपयोग करके एक बहु रेखीय प्रतिगमन मॉडल बनाते हैं।

फिर हम यह समझने के लिए मॉडल का उपयोग कर सकते हैं कि विज्ञापन, प्रत्येक अतिरिक्त कर्मचारी और प्रत्येक अतिरिक्त अधिग्रहण पर खर्च किए गए प्रत्येक अतिरिक्त डॉलर के साथ कुल वार्षिक राजस्व में कितना बदलाव होता है (औसतन)।

भविष्यवाणी का एक उदाहरण:

हम समान एकाधिक रैखिक प्रतिगमन मॉडल का निर्माण कर सकते हैं और इसका उपयोग कंपनी के कुल विपणन खर्च, कर्मचारियों की संख्या और कुल अधिग्रहण के आधार पर कंपनी के वार्षिक राजस्व की भविष्यवाणी करने के लिए कर सकते हैं।

उदाहरण के लिए, हम उस कंपनी के वार्षिक राजस्व की भविष्यवाणी करने के लिए मॉडल का उपयोग कर सकते हैं जो विज्ञापन पर $25 मिलियन खर्च करती है, जिसमें 40 कर्मचारी हैं और जिसने 2 अधिग्रहण किए हैं।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल सांख्यिकी में समझने के लिए महत्वपूर्ण शब्दों पर अतिरिक्त जानकारी प्रदान करते हैं:

वर्णनात्मक या अनुमानात्मक आँकड़े: क्या अंतर है?
माप स्तर: नाममात्र, क्रमसूचक, अंतराल और अनुपात
गुणात्मक और मात्रात्मक चर: क्या अंतर है?