एफ डिस्ट्रीब्यूशन का उपयोग करके कॉन्फिडेंस इंटरवल कैसे बनाएं

यह निर्धारित करने के लिए कि क्या दो आबादी के प्रसरण बराबर हैं, हम प्रसरण अनुपात σ ² ₁ / σ ² ₂ की गणना कर सकते हैं, जहां σ ² ₁ जनसंख्या 1 का प्रसरण है और σ ² ₂ जनसंख्या 2 का प्रसरण है।

वास्तविक जनसंख्या विचरण अनुपात का अनुमान लगाने के लिए, हम आम तौर पर प्रत्येक जनसंख्या से एक सरल यादृच्छिक नमूना लेते हैं और नमूना विचरण अनुपात, एस ₁ ² / एस ₂ ² की गणना करते हैं, जहां एस ₁ ² और एस ₂ ² नमूना 1 और नमूने के लिए नमूना भिन्नताएं हैं। . क्रमशः 2.

यह परीक्षण मानता है कि s ₁ ² और s ₂ ² की गणना सामान्य रूप से वितरित आबादी से n ₁ और n ₂ आकार के स्वतंत्र नमूनों से की जाती है।

यह अनुपात एक से जितना अधिक होगा, जनसंख्या के भीतर असमान भिन्नताओं के प्रमाण उतने ही मजबूत होंगे।

σ ² ₁ / σ ² ₂ के लिए (1-α)100% विश्वास अंतराल को इस प्रकार परिभाषित किया गया है:

(एस ₁ ² / एस ₂ ² ) * एफ _{एन 1 -1, एन 2 -1, α/2} ≤ σ ² ₁ / σ ² ₂ ≤ (एस ₁ ² / एस _{2 2} ² ) * एफ _{एन 2 -1, एन 1 -1, α/2}

जहाँ F _{n 2 -1, n 1 -1, α/2} और F _{n 1 -1, n 2 -1, α/2}   चुने गए महत्व स्तर α के लिए वितरण F के महत्वपूर्ण मान हैं।

निम्नलिखित उदाहरण बताते हैं कि तीन अलग-अलग तरीकों का उपयोग करके σ ² ₁ / σ ² ₂ के लिए आत्मविश्वास अंतराल कैसे बनाया जाए:

• हाथ से
• माइक्रोसॉफ्ट एक्सेल का प्रयोग करें
• आर सांख्यिकीय सॉफ्टवेयर का उपयोग

निम्नलिखित प्रत्येक उदाहरण के लिए, हम निम्नलिखित जानकारी का उपयोग करेंगे:

• α = 0.05
• एन ₁ = 16
• _n2 = 11
• एस ₁ ² =28.2
• एस ₂ ² = 19.3

मैन्युअल रूप से एक विश्वास अंतराल बनाना

σ ² ₁ / σ ² ₂ के लिए आत्मविश्वास अंतराल की मैन्युअल रूप से गणना करने के लिए, हम बस हमारे पास मौजूद संख्याओं को आत्मविश्वास अंतराल सूत्र में प्लग करेंगे:

(एस ₁ ² / एस ₂ ² ) * एफ _{एन1-1, एन2-1,α/2} ≤ σ ² ₁ / σ ² ₂ ≤ (एस ₁ ² / एस ₂ ² ) * एफ _{एन2-1, एन1-1, α/2}

एकमात्र संख्याएँ जो हमें याद आ रही हैं वे महत्वपूर्ण मूल्य हैं। सौभाग्य से, हम वितरण तालिका F में इन महत्वपूर्ण मानों का पता लगा सकते हैं:

एफ _{एन2-1, एन1-1, α/2} = एफ _{10, 15, 0.025} = 3.0602

एफ _{एन1-1, एन2-1, α/2} = 1/ एफ _{15, 10, 0.025} = 1 / 3.5217 = 0.2839

(टेबल पर ज़ूम इन करने के लिए क्लिक करें)

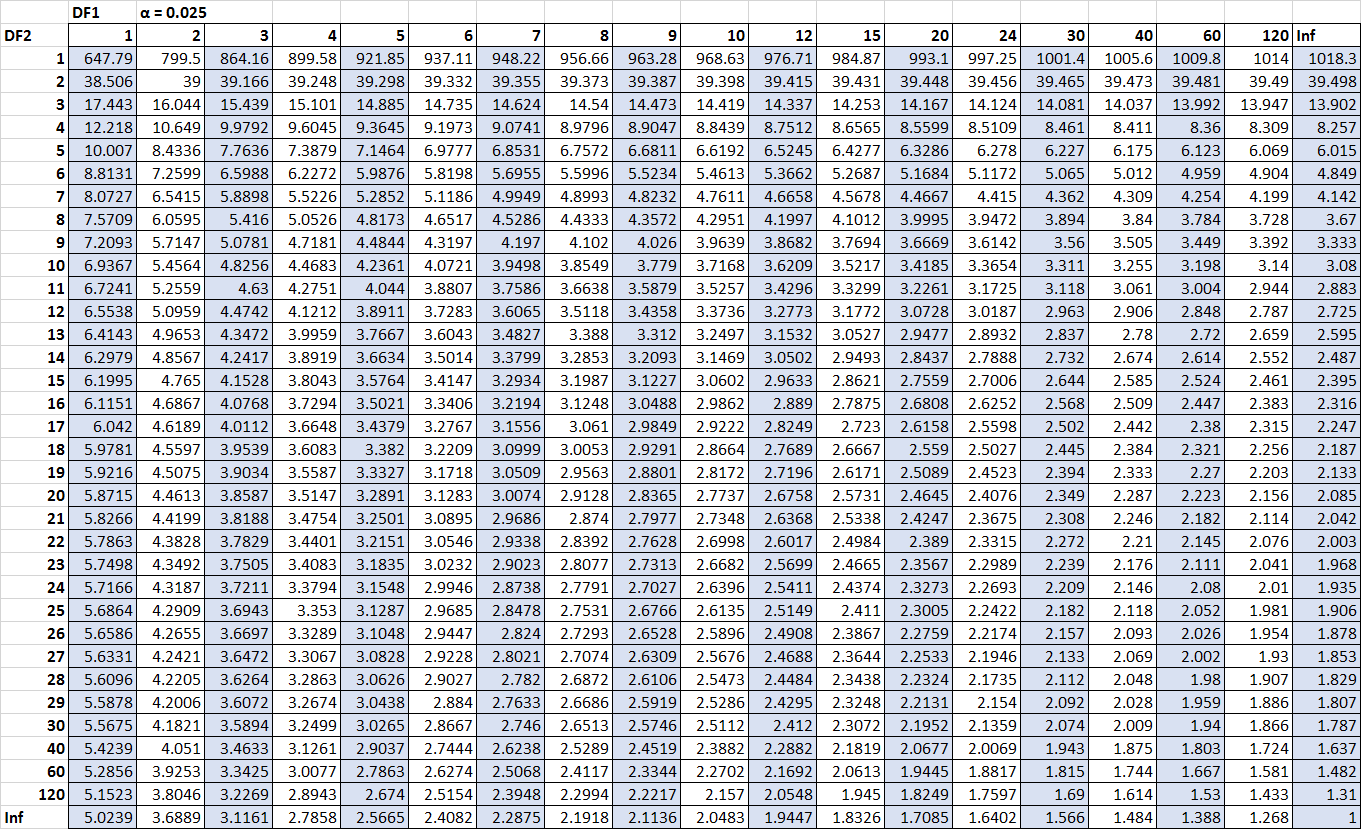
अब हम सभी नंबरों को कॉन्फिडेंस फॉर्मूला अंतराल में प्लग कर सकते हैं:

(एस ₁ ² / एस ₂ ² ) * एफ _{एन1-1, एन2-1,α/2} ≤ σ ² ₁ / σ ² ₂ ≤ (एस ₁ ² / एस ₂ ² ) * एफ _{एन2-1, एन1-1, α/2}

(28.2 / 19.3) * (0.2839) ≤ σ ² ₁ / σ ² ₂ ≤ (28.2 / 19.3) * (3.0602)

0.4148 ≤ σ ² ₁ / σ ² ₂ ≤ 4.4714

इस प्रकार, जनसंख्या भिन्नता के अनुपात के लिए 95% विश्वास अंतराल (0.4148, 4.4714) है।

एक्सेल का उपयोग करके कॉन्फिडेंस इंटरवल बनाना

निम्नलिखित छवि दिखाती है कि एक्सेल में जनसंख्या विचरण अनुपात के लिए 95% विश्वास अंतराल की गणना कैसे करें। विश्वास अंतराल की निचली और ऊपरी सीमाएँ कॉलम E में दिखाई गई हैं और निचली और ऊपरी सीमाएँ खोजने के लिए उपयोग किया जाने वाला सूत्र कॉलम F में दिखाया गया है:

इस प्रकार, जनसंख्या भिन्नता के अनुपात के लिए 95% विश्वास अंतराल (0.4148, 4.4714) है। यह उससे मेल खाता है जो हमें तब मिला जब हमने मैन्युअल रूप से कॉन्फिडेंस अंतराल की गणना की।

आर का उपयोग करके कॉन्फिडेंस इंटरवल बनाना

निम्नलिखित कोड दर्शाता है कि आर में जनसंख्या भिन्नता के अनुपात के लिए 95% विश्वास अंतराल की गणना कैसे करें:

 #define significance level, sample sizes, and sample variances
alpha <- .05
n1 <- 16
n2 <- 11
var1 <- 28.2
var2 <- 19.3

#define F critical values
upper_crit <- 1/qf(alpha/2, n1-1, n2-1)
lower_crit <- qf(alpha/2, n2-1, n1-1)

#find confidence interval
lower_bound <- (var1/var2) * lower_crit
upper_bound <- (var1/var2) * upper_crit

#output confidence interval
paste0("(", lower_bound, ", ", upper_bound, " )")

#[1] "(0.414899337980266, 4.47137571035219 )"

इस प्रकार, जनसंख्या भिन्नता के अनुपात के लिए 95% विश्वास अंतराल (0.4148, 4.4714) है। यह उससे मेल खाता है जो हमें तब मिला जब हमने मैन्युअल रूप से कॉन्फिडेंस अंतराल की गणना की।

अतिरिक्त संसाधन

एफ डिस्ट्रीब्यूशन बोर्ड को कैसे पढ़ें
Excel में महत्वपूर्ण मान F कैसे ज्ञात करें