आरएमएसई बनाम आर-स्क्वेर्ड: आपको किस मीट्रिक का उपयोग करना चाहिए?

प्रतिगमन मॉडल का उपयोग एक या अधिक भविष्यवक्ता चर और एक प्रतिक्रिया चर के बीच संबंध को मापने के लिए किया जाता है।

जब भी हम एक प्रतिगमन मॉडल फिट करते हैं, तो हम यह समझना चाहते हैं कि मॉडल डेटा को कितनी अच्छी तरह “फिट” करता है। दूसरे शब्दों में, प्रतिक्रिया चर के मूल्य की भविष्यवाणी करने के लिए मॉडल भविष्यवक्ता चर के मूल्यों का उपयोग करने में कितना सक्षम है?

दो मीट्रिक जिनका उपयोग सांख्यिकीविद् अक्सर यह निर्धारित करने के लिए करते हैं कि कोई मॉडल डेटा सेट में कितनी अच्छी तरह फिट बैठता है, मूल माध्य वर्ग त्रुटि (आरएमएसई) और आर वर्ग ( ^{आर 2} ) हैं, जिनकी गणना निम्नानुसार की जाती है:

आरएमएसई : एक मीट्रिक जो हमें बताती है कि अनुमानित मान डेटा सेट में देखे गए मानों से औसतन कितनी दूर हैं। आरएमएसई जितना कम होगा, मॉडल डेटा सेट में उतना ही बेहतर फिट होगा।

इसकी गणना इस प्रकार की जाती है:

आरएमएसई = √ Σ(पी _आई – ओ _आई ) ² / एन

सोना:

• Σ एक प्रतीक है जिसका अर्थ है “योग”
• P _i, ^ith अवलोकन के लिए अनुमानित मान है
• O _{i i} ^वें अवलोकन के लिए प्रेक्षित मान है
• n नमूना आकार है

आर ² : एक मीट्रिक जो हमें बताती है कि प्रतिगमन मॉडल के प्रतिक्रिया चर में कितना भिन्नता भविष्यवक्ता चर द्वारा समझाया जा सकता है। यह मान 0 और 1 के बीच है। R ² मान जितना अधिक होगा, मॉडल डेटा के सेट में उतना ही बेहतर फिट होगा।

इसकी गणना इस प्रकार की जाती है:

^आर2 = 1 – (आरएसएस/टीएसएस)

सोना:

• आरएसएस अवशेषों के वर्गों के योग का प्रतिनिधित्व करता है
• टीएसएस वर्गों के कुल योग का प्रतिनिधित्व करता है

आरएमएसई बनाम आर ² : आपको किस मीट्रिक का उपयोग करना चाहिए?

डेटा सेट में किसी मॉडल की फिट का मूल्यांकन करते समय, आरएमएसई मान और आर ² मान दोनों की गणना करना उपयोगी होता है, क्योंकि प्रत्येक मीट्रिक हमें कुछ अलग बताता है।

एक ओर, आरएमएसई हमें प्रतिगमन मॉडल द्वारा बनाए गए अनुमानित मूल्य और वास्तविक मूल्य के बीच की विशिष्ट दूरी बताता है।

दूसरी ओर, आर ² हमें बताता है कि भविष्यवक्ता चर किस हद तक प्रतिक्रिया चर में भिन्नता को समझा सकते हैं।

उदाहरण के लिए, मान लें कि हमारे पास निम्नलिखित डेटासेट हैं जो एक निश्चित शहर में घरों के बारे में जानकारी प्रदर्शित करते हैं:

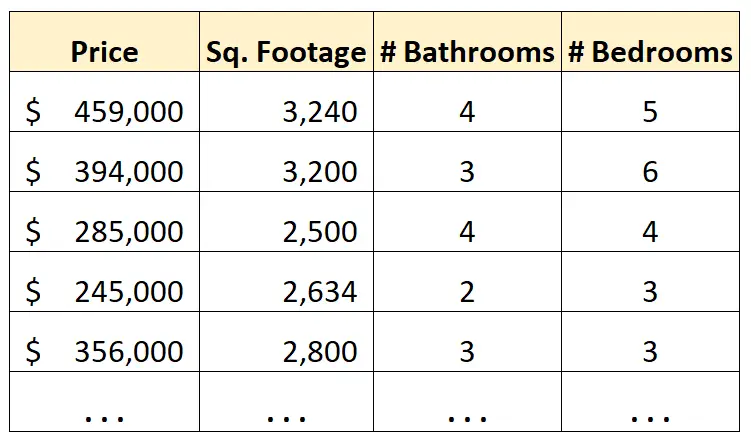
अब मान लीजिए कि हम एक घर की कीमत का अनुमान लगाने के लिए वर्ग फुटेज, बाथरूमों की संख्या और शयनकक्षों की संख्या का उपयोग करना चाहते हैं।

हम निम्नलिखित प्रतिगमन मॉडल को अनुकूलित कर सकते हैं:

कीमत = β ₀ + β ₁ (वर्ग फ़ुटेज) + β ₂ (# बाथरूम) + β ₃ (# शयनकक्ष)

अब मान लीजिए कि हम इस मॉडल को फिट करते हैं और फिर मॉडल की फिट की अच्छाई का मूल्यांकन करने के लिए निम्नलिखित मैट्रिक्स की गणना करते हैं:

• आरएमएसई : 14.342
• ^आर2 : 0.856

आरएमएसई मूल्य हमें बताता है कि मॉडल की अनुमानित घर की कीमत और वास्तविक घर की कीमत के बीच औसत अंतर $14,342 है।

आर ² मान हमें बताता है कि मॉडल के भविष्यवक्ता चर (वर्ग फुटेज, बाथरूम की संख्या और शयनकक्षों की संख्या) आवास की कीमतों में 85.6% भिन्नता को समझाने में सक्षम हैं।

यह निर्धारित करने के लिए कि ये मान “अच्छे” हैं या नहीं, हम इन मापों की तुलना वैकल्पिक मॉडल से कर सकते हैं।

उदाहरण के लिए, मान लीजिए कि हम एक अन्य प्रतिगमन मॉडल फिट करते हैं जो भविष्यवक्ता चर के एक अलग सेट का उपयोग करता है और उस मॉडल के लिए निम्नलिखित मैट्रिक्स की गणना करता है:

• आरएमएसई : 19.355
• ^आर2 : 0.765

हम देख सकते हैं कि इस मॉडल का आरएमएसई मूल्य पिछले मॉडल की तुलना में अधिक है। यह भी देखा जा सकता है कि इस मॉडल की ^R2 वैल्यू पिछले मॉडल की तुलना में कम है। यह हमें बताता है कि यह मॉडल पिछले मॉडल की तुलना में डेटा पर कम फिट बैठता है।

सारांश

इस लेख में उठाए गए मुख्य बिंदु इस प्रकार हैं:

• आरएमएसई और आर ² यह निर्धारित करते हैं कि एक प्रतिगमन मॉडल डेटा सेट में कितनी अच्छी तरह फिट बैठता है।
• आरएमएसई हमें बताता है कि एक प्रतिगमन मॉडल निरपेक्ष रूप से प्रतिक्रिया चर के मूल्य की कितनी अच्छी तरह भविष्यवाणी कर सकता है, जबकि आर ² हमें बताता है कि एक मॉडल प्रतिशत के संदर्भ में प्रतिक्रिया चर के मूल्य की कितनी अच्छी तरह भविष्यवाणी कर सकता है।
• किसी दिए गए मॉडल के लिए RMSE और ^R2 दोनों की गणना करना उपयोगी है क्योंकि प्रत्येक मीट्रिक हमें उपयोगी जानकारी देता है।

अतिरिक्त संसाधन

एकाधिक रेखीय प्रतिगमन का परिचय
आर बनाम आर-स्क्वायर: क्या अंतर है?
एक अच्छा आर-वर्ग मान क्या है?