आर में टुकड़े-टुकड़े प्रतिगमन कैसे करें (चरण दर चरण)
टुकड़े-टुकड़े प्रतिगमन एक प्रतिगमन विधि है जिसका उपयोग हम अक्सर तब करते हैं जब डेटा सेट में स्पष्ट “ब्रेकप्वाइंट” होते हैं।
निम्नलिखित चरण-दर-चरण उदाहरण दिखाता है कि आर में टुकड़े-टुकड़े प्रतिगमन कैसे करें।
चरण 1: डेटा बनाएं
सबसे पहले, आइए निम्नलिखित डेटा फ़्रेम बनाएं:
#view DataFrame df <- data. frame (x=c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16), y=c(2, 4, 5, 6, 8, 10, 12, 13, 15, 19, 24, 28, 31, 34, 39, 44)) #view first six rows of data frame head(df) xy 1 1 2 2 2 4 3 3 5 4 4 6 5 5 8 6 6 10
चरण 2: डेटा को विज़ुअलाइज़ करें
इसके बाद, आइए डेटा को विज़ुअलाइज़ करने के लिए एक स्कैटरप्लॉट बनाएं:
#create scatterplot of x vs. y plot(df$x, df$y, pch= 16 , col=' steelblue ')
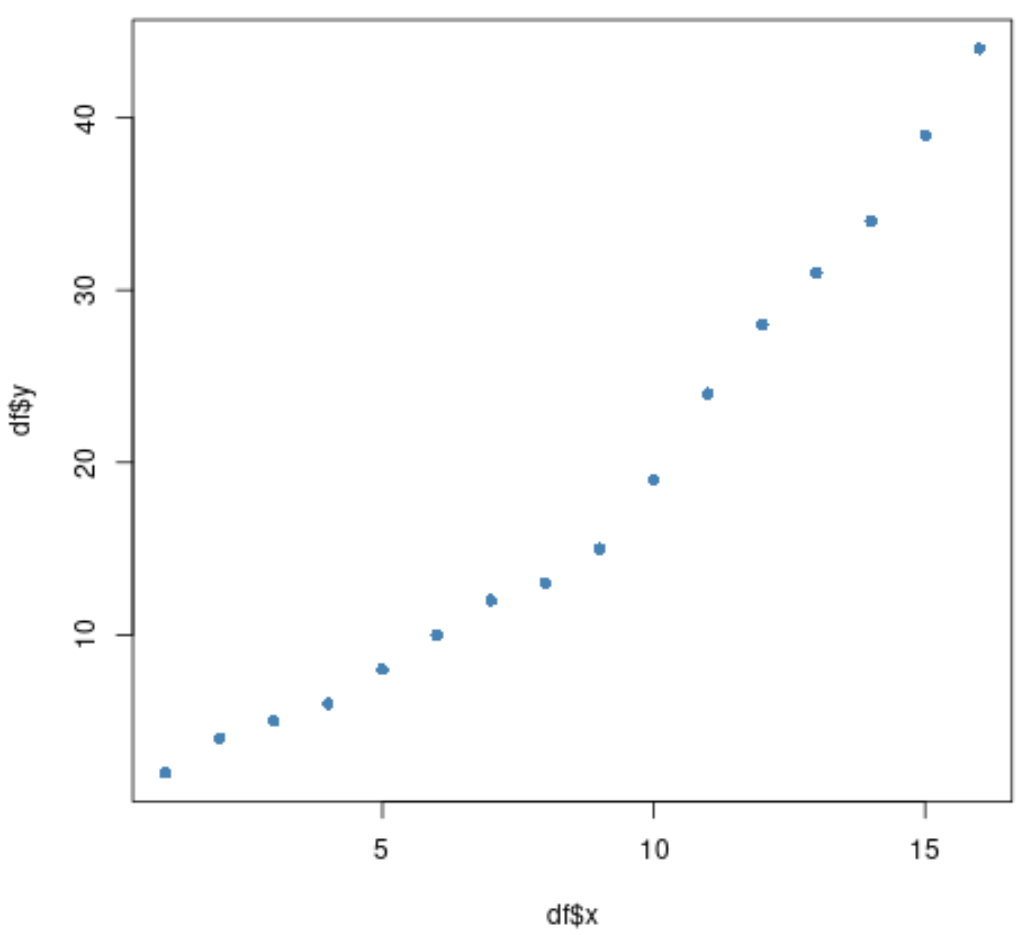
हम देख सकते हैं कि x और y के बीच का संबंध x = 9 के आसपास अचानक बदलता प्रतीत होता है।
चरण 3: टुकड़ेवार प्रतिगमन मॉडल को फिट करें
हम अपने डेटासेट में टुकड़े-टुकड़े प्रतिगमन मॉडल को फिट करने के लिए आर में खंडित पैकेज से खंडित() फ़ंक्शन का उपयोग कर सकते हैं:
library (segmented) #fit simple linear regression model fit <- lm(y ~ x, data=df) #fit piecewise regression model to original model, estimating a breakpoint at x=9 segmented. fit <- segmented(fit, seg.Z = ~x, psi= 9 ) #view summary of segmented model summary( segmented.fit ) Call: segmented.lm(obj = fit, seg.Z = ~x, psi = 9) Estimated Break-Point(s): East. St.Err psi1.x 8.762 0.26 Meaningful coefficients of the linear terms: Estimate Std. Error t value Pr(>|t|) (Intercept) 0.32143 0.48343 0.665 0.519 x 1.59524 0.09573 16.663 1.16e-09 *** U1.x 2.40476 0.13539 17.762 NA --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 0.6204 on 12 degrees of freedom Multiple R-Squared: 0.9983, Adjusted R-squared: 0.9978 Convergence achieved in 2 iter. (rel. changes 0)
खंडित() फ़ंक्शन x = 8.762 पर एक ब्रेकपॉइंट का पता लगाता है।
फिट किया गया टुकड़ा-वार प्रतिगमन मॉडल है:
यदि x ≤ 8.762: y = 0.32143 + 1.59524*(x)
यदि x > 8.762: y = 0.32143 + 1.59524*(8.762) + (1.59524+2.40476)*(x-8.762)
उदाहरण के लिए, मान लीजिए कि हमारे पास x = 5 का मान है। अनुमानित मूल्य होगा:
- y = 0.32143 + 1.59524*(x)
- y = 0.32143 + 1.59524*(5)
- y = 8.297
या मान लीजिए कि हमारे पास x = 12 का मान है। अनुमानित मूल्य होगा:
- y = 0.32143 + 1.59524*(8.762) + (1.59524+2.40476)*(12-8.762)
- वाई = 27.25
चरण 4: अंतिम टुकड़ेवार प्रतिगमन मॉडल की कल्पना करें
हम अपने मूल डेटा के शीर्ष पर अंतिम टुकड़े-टुकड़े प्रतिगमन मॉडल की कल्पना करने के लिए निम्नलिखित कोड का उपयोग कर सकते हैं:
#plot original data plot(df$x, df$y, pch= 16 , col=' steelblue ') #add segmented regression model plot(segmented. fit , add= T )
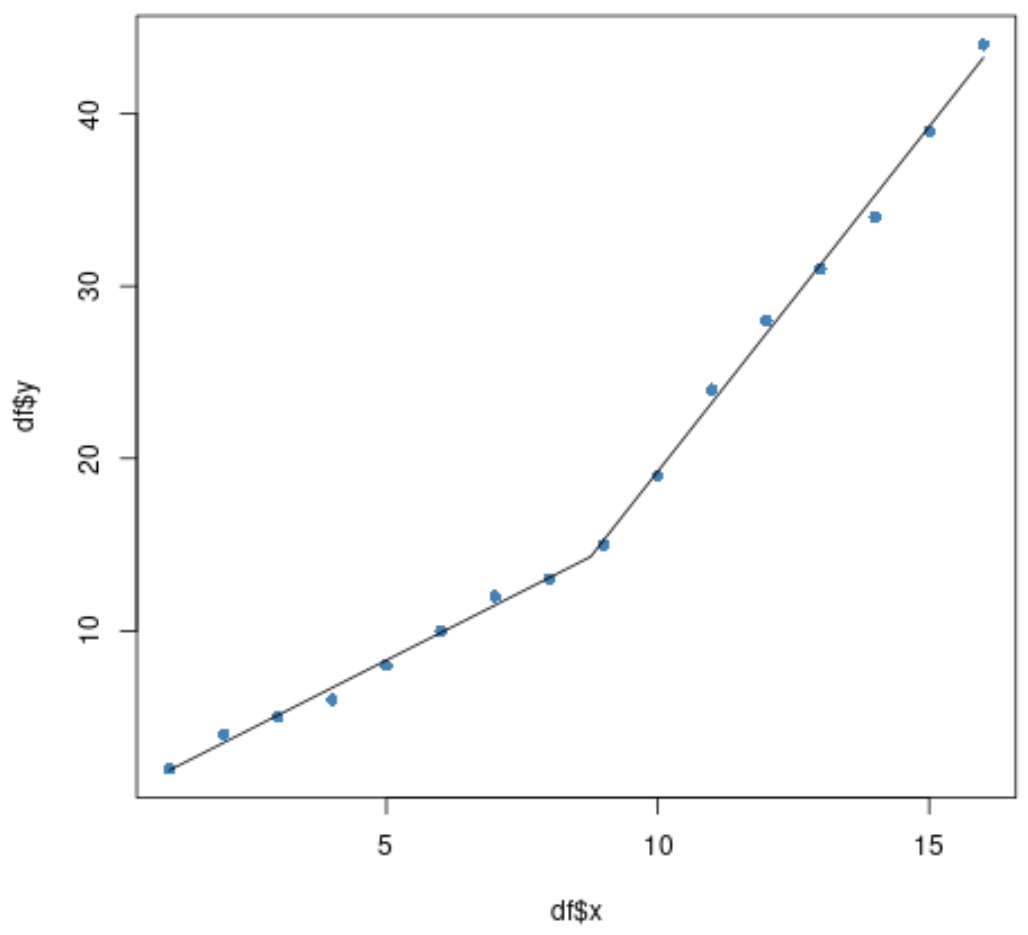
ऐसा प्रतीत होता है कि टुकड़े-टुकड़े प्रतिगमन मॉडल डेटा को काफी अच्छी तरह से फिट बैठता है।
अतिरिक्त संसाधन
निम्नलिखित ट्यूटोरियल आर में प्रतिगमन मॉडल के बारे में अतिरिक्त जानकारी प्रदान करते हैं:
आर में सरल रैखिक प्रतिगमन कैसे करें
आर में मल्टीपल लीनियर रिग्रेशन कैसे करें
आर में लॉजिस्टिक रिग्रेशन कैसे करें
आर में क्वांटाइल रिग्रेशन कैसे करें
आर में भारित प्रतिगमन कैसे करें