आर में एक द्विचर सामान्य वितरण का अनुकरण और प्लॉट कैसे करें

आँकड़ों में, दो चर एक द्विचर सामान्य वितरण का अनुसरण करते हैं यदि उन्हें एक साथ जोड़ने पर एक सामान्य वितरण होता है।

यह ट्यूटोरियल बताता है कि R में निम्नलिखित कार्य कैसे करें:

• एक द्विचर सामान्य वितरण का अनुकरण करें
• एक समोच्च प्लॉट (2D प्लॉट) का उपयोग करके एक द्विचर सामान्य वितरण प्लॉट करें
• एक सतह प्लॉट (3डी प्लॉट) का उपयोग करके एक द्विचर सामान्य वितरण प्लॉट करें

चल दर!

उदाहरण 1: आर में एक द्विचर सामान्य वितरण का अनुकरण करें

R में द्विचर सामान्य वितरण का अनुकरण करने का सबसे सरल तरीका MASS पैकेज से mvrnorm() फ़ंक्शन का उपयोग करना है।

निम्नलिखित कोड दिखाता है कि व्यवहार में द्विचर सामान्य वितरण का अनुकरण करने के लिए इस फ़ंक्शन का उपयोग कैसे करें:

 library (MASS)

#make this example reproducible
set. seed ( 0 )

#simulate bivariate normal distribution
bivariate_data <- as. data . frame (mvrnorm(n= 100 ,
                                        mu=c(0, 0),
                                        Sigma=matrix(c(5, 3, 4, 4), ncol= 2 )))

#view first six rows of bivariate dataset
head(bivariate_data)

           V1 V2
1 -2.03600343 -2.9623059
2 0.07719131 1.2948982
3 -3.26729701 -1.7928069
4 -2.62985132 -2.3015471
5 -1.75126215 0.3056698
6 3.67698436 2.2020238

यहां बताया गया है कि mvrnorm() फ़ंक्शन का प्रत्येक तर्क क्या करता है:

• n : नमूना आकार को परिभाषित करता है
• म्यू : प्रत्येक चर का औसत परिभाषित करता है
• सिग्मा : दो चरों के सहप्रसरण मैट्रिक्स को परिभाषित करता है

अंतिम परिणाम दो चर वाला एक डेटा फ़्रेम है जो एक साथ जोड़े जाने पर सामान्य वितरण का अनुसरण करता है।

उदाहरण 2: एक द्विचर सामान्य वितरण आलेखित करना

आर में द्विचर सामान्य वितरण को प्लॉट करने का सबसे आसान तरीका mnormt() पैकेज में फ़ंक्शन का उपयोग करना है।

उदाहरण के लिए, हम एक समोच्च प्लॉट बनाने के लिए इस पैकेज के कॉन्टूर() फ़ंक्शन का उपयोग कर सकते हैं, जो द्विचर सामान्य वितरण का 2डी विज़ुअलाइज़ेशन प्रदान करता है:

 library (mnormt)

#make this example reproducible
set. seed ( 0 )

#create bivariate normal distribution
x <- seq(-3, 3, 0.1) 
y <- seq(-3, 3, 0.1)
mu <- c(0, 0)
sigma <- matrix(c(2, -1, -1, 2), nrow= 2 )
f <- function(x, y) dmnorm(cbind(x, y), mu, sigma)
z <- outer(x, y, f)

#create contour plot
contour(x, y, z)

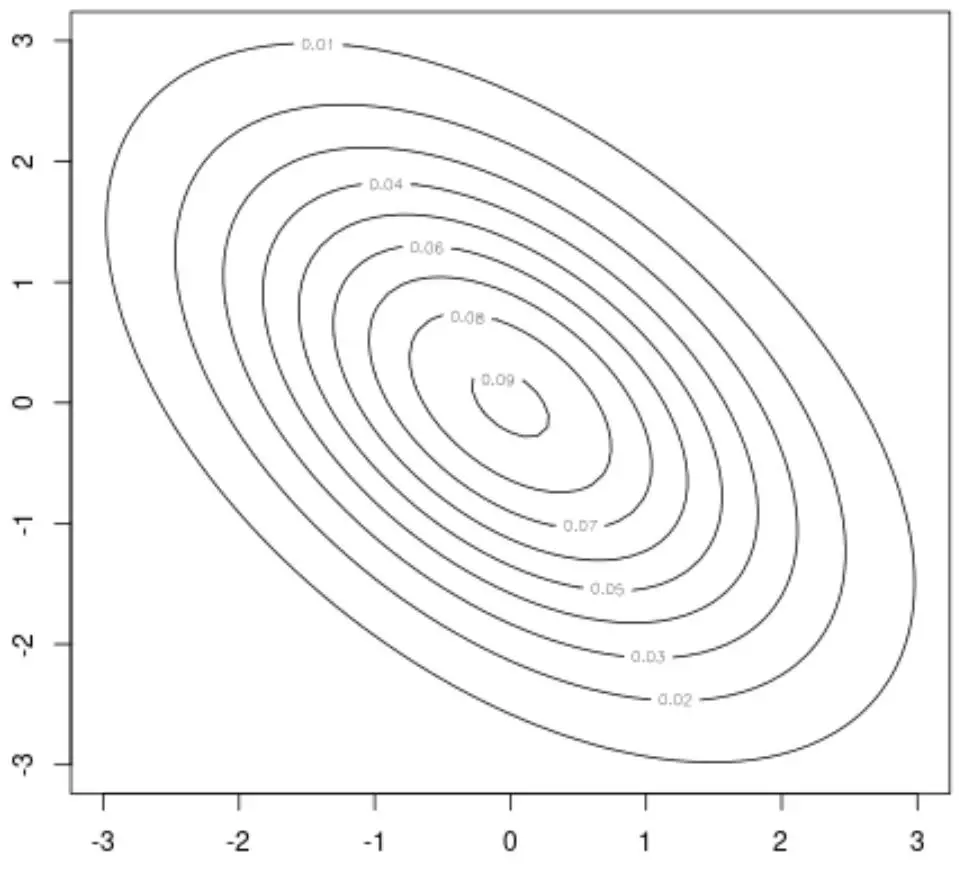
हम सतह प्लॉट बनाने के लिए persp() फ़ंक्शन का भी उपयोग कर सकते हैं, जो द्विचर सामान्य वितरण का 3D विज़ुअलाइज़ेशन प्रदान करता है:

 library (mnormt)

#make this example reproducible
set. seed ( 0 )

#create bivariate normal distribution
x <- seq(-3, 3, 0.1) 
y <- seq(-3, 3, 0.1)
mu <- c(0, 0)
sigma <- matrix(c(2, -1, -1, 2), nrow= 2 )
f <- function(x, y) dmnorm(cbind(x, y), mu, sigma)
z <- outer(x, y, f)

#create surface plot
persp(x, y, z, theta= -30 , phi= 25 , expand= 0.6 , ticktype=' detailed ')

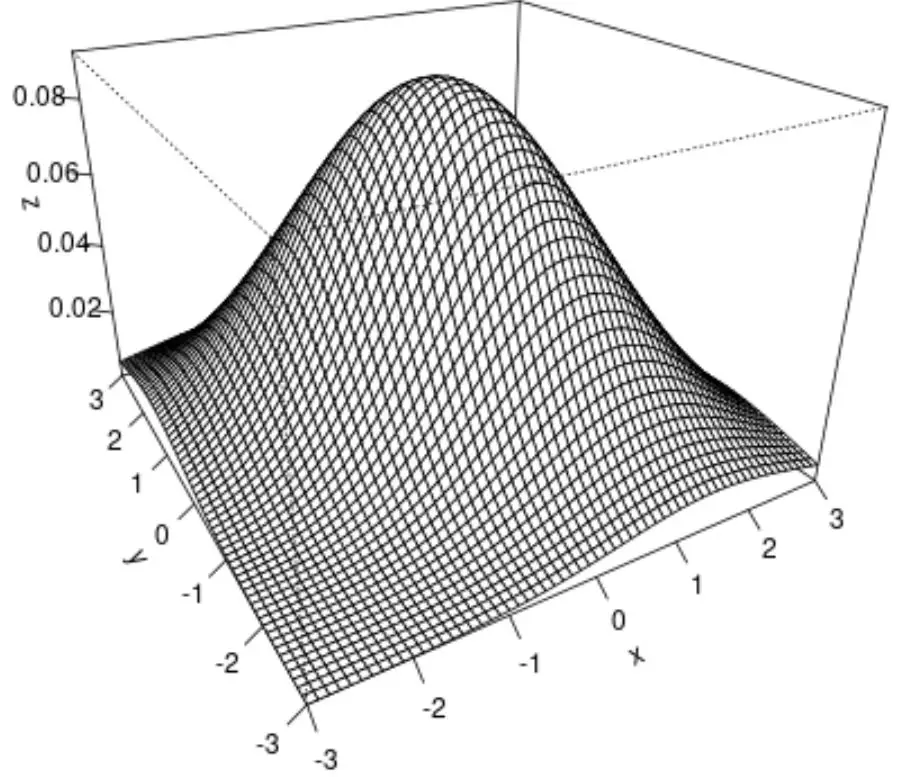
यहां बताया गया है कि persp() फ़ंक्शन का प्रत्येक तर्क क्या करता है:

• थीटा, फाई : देखने की दिशा के कोण सेट करता है।
• विस्तार : z अक्ष के आकार को नियंत्रित करता है।
• टिकटाइप : अक्षों पर टिकों की उपस्थिति को नियंत्रित करता है।

अंतिम परिणाम द्विचर सामान्य वितरण का एक 3डी सतह प्लॉट है।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल बताते हैं कि आर में अन्य संभाव्यता वितरण का उपयोग कैसे करें:

आर में सामान्य वितरण का उपयोग कैसे करें
R में द्विपद वितरण का उपयोग कैसे करें
आर में पॉइसन वितरण का उपयोग कैसे करें
आर में बहुपद वितरण का उपयोग कैसे करें