R में phi गुणांक की गणना कैसे करें
फाई गुणांक (कभी-कभी माध्य वर्ग आकस्मिकता गुणांक कहा जाता है) दो बाइनरी चर के बीच संबंध का एक माप है।
दो यादृच्छिक चर x और y के लिए दी गई 2×2 तालिका के लिए:

फाई गुणांक की गणना निम्नानुसार की जा सकती है:
Φ = (एडी-बीसी) / √ (ए+बी)(सी+डी)(ए+सी)(बी+डी)
उदाहरण: R में Phi गुणांक की गणना
मान लीजिए हम जानना चाहते हैं कि किसी राजनीतिक दल की प्राथमिकता के साथ लिंग का संबंध है या नहीं। इसलिए हम 25 मतदाताओं का एक सरल यादृच्छिक नमूना लेते हैं और उनसे एक राजनीतिक दल के लिए उनकी पसंद के बारे में पूछते हैं।
निम्नलिखित तालिका सर्वेक्षण के परिणाम प्रस्तुत करती है:
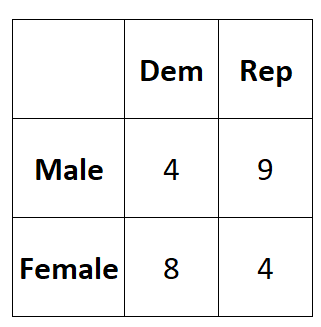
हम इस डेटा को R में 2×2 मैट्रिक्स में दर्ज करने के लिए निम्नलिखित कोड का उपयोग कर सकते हैं:
#create 2x2 table data = matrix(c(4, 8, 9, 4), nrow = 2 ) #view dataset data [,1] [,2] [1,] 4 9 [2,] 8 4
फिर हम दो चरों के बीच Phi गुणांक की गणना करने के लिए psych पैकेज से phi() फ़ंक्शन का उपयोग कर सकते हैं:
#load psych package library (psych) #calculate Phi Coefficient phi(data) [1] -0.36
Phi गुणांक -0.36 निकला।
ध्यान दें कि phi फ़ंक्शन डिफ़ॉल्ट रूप से 2 अंकों तक पूर्णांकित होता है, लेकिन आप फ़ंक्शन को जितने चाहें उतने अंकों तक पूर्णांकित करने के लिए निर्दिष्ट कर सकते हैं:
#calculate Phi Coefficient and round to 6 digits phi(data, digits = 6 ) [1] -0.358974
फाई गुणांक की व्याख्या कैसे करें
पियर्सन सहसंबंध गुणांक के समान, फाई गुणांक -1 और 1 के बीच मान लेता है जहां:
- -1 दो चरों के बीच पूर्णतया नकारात्मक संबंध दर्शाता है।
- 0 दो चरों के बीच कोई संबंध नहीं दर्शाता है।
- 1 दो चरों के बीच पूर्णतः सकारात्मक संबंध दर्शाता है।
सामान्य तौर पर, Phi गुणांक शून्य से जितना अधिक होता है, दोनों चर के बीच संबंध उतना ही मजबूत होता है।
दूसरे शब्दों में, Phi गुणांक शून्य से जितना दूर होगा, दोनों चरों के बीच किसी प्रकार के व्यवस्थित पैटर्न का उतना ही अधिक प्रमाण होगा।
अतिरिक्त संसाधन
फाई गुणांक का परिचय
फाई गुणांक कैलकुलेटर