आर में तिरछापन और कर्टोसिस की गणना कैसे करें

आंकड़ों में, तिरछापन और कुर्टोसिस वितरण के आकार को मापने के दो तरीके हैं।

विषमता किसी वितरण की विषमता का माप है। यह मान धनात्मक अथवा ऋणात्मक हो सकता है।

• नकारात्मक तिरछापन इंगित करता है कि पूंछ वितरण के बाईं ओर है, जो अधिक नकारात्मक मूल्यों की ओर बढ़ती है।
• एक सकारात्मक तिरछा इंगित करता है कि पूंछ वितरण के दाईं ओर है, जो अधिक सकारात्मक मूल्यों की ओर बढ़ती है।
• शून्य का मान इंगित करता है कि वितरण में कोई विषमता नहीं है, जिसका अर्थ है कि वितरण पूरी तरह से सममित है।

कर्टोसिस इस बात का माप है कि कोई वितरण सामान्य वितरण की तुलना में भारी है या हल्का।

• सामान्य वितरण का कुर्टोसिस 3 है।
• यदि किसी दिए गए वितरण में कर्टोसिस 3 से कम है, तो इसे प्लेकर्टिक कहा जाता है, जिसका अर्थ है कि यह सामान्य वितरण की तुलना में कम और कम चरम आउटलेर उत्पन्न करता है।
• यदि किसी दिए गए वितरण में कर्टोसिस 3 से अधिक है, तो इसे लेप्टोकर्टिक कहा जाता है, जिसका अर्थ है कि यह सामान्य वितरण की तुलना में अधिक आउटलेर्स उत्पन्न करता है।

नोट: कुछ सूत्र (फिशर परिभाषा) सामान्य वितरण के साथ तुलना करना आसान बनाने के लिए कर्टोसिस से 3 घटाते हैं। इस परिभाषा का उपयोग करते हुए, एक वितरण में सामान्य वितरण की तुलना में अधिक कर्टोसिस होगा यदि उसका कर्टोसिस मान 0 से अधिक हो।

यह ट्यूटोरियल बताता है कि आर में दिए गए डेटासेट की तिरछापन और कर्टोसिस दोनों की गणना कैसे करें।

उदाहरण: आर में तिरछापन और चपटापन

मान लीजिए हमारे पास निम्नलिखित डेटा सेट है:

 data = c(88, 95, 92, 97, 96, 97, 94, 86, 91, 95, 97, 88, 85, 76, 68)

हम हिस्टोग्राम बनाकर इस डेटासेट में मूल्यों के वितरण की शीघ्रता से कल्पना कर सकते हैं:

 hist(data, col=' steelblue ') 

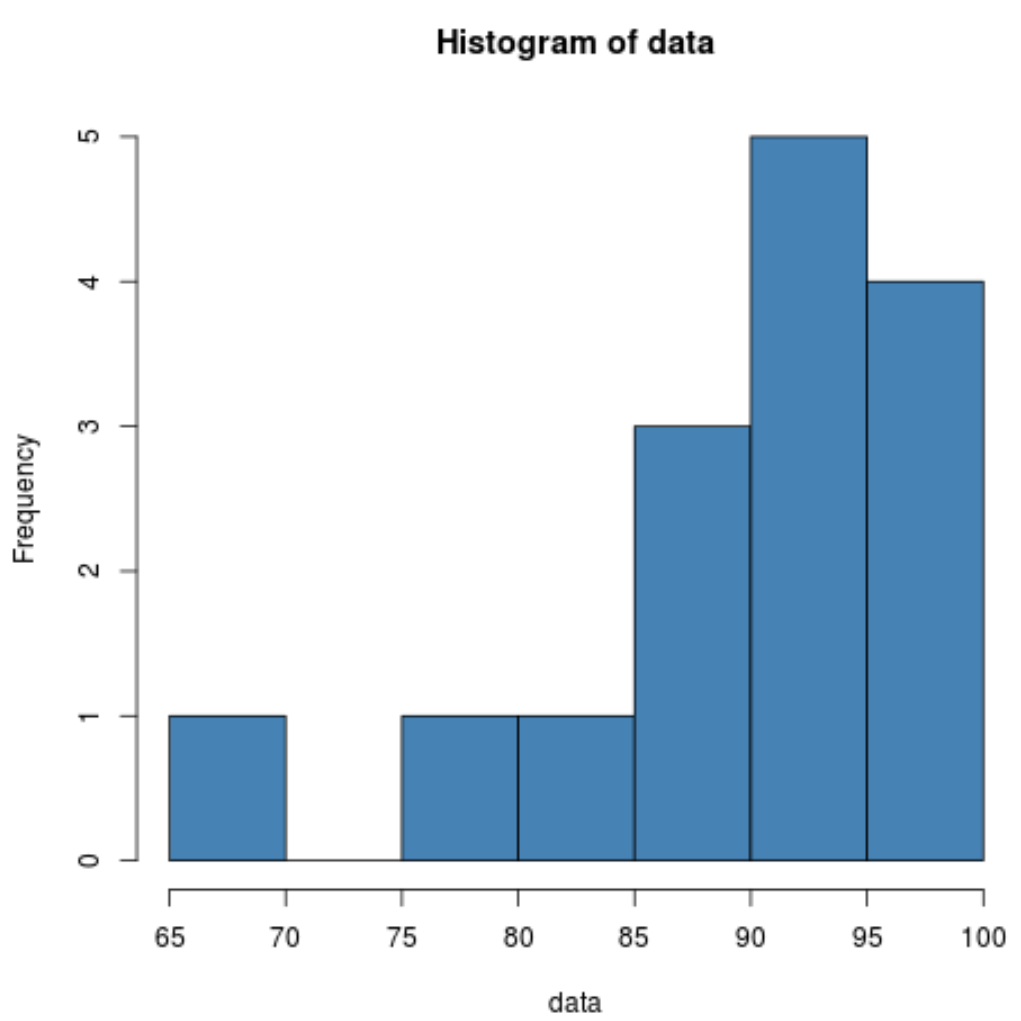
हिस्टोग्राम हमें दिखाता है कि वितरण बाईं ओर झुका हुआ प्रतीत होता है। अर्थात्, मूल्यों का एक बड़ा हिस्सा वितरण के दाईं ओर केंद्रित है।

इस डेटासेट की विषमता और कर्टोसिस की गणना करने के लिए, हम आर में पल लाइब्रेरी से तिरछापन () और कर्टोसिस () फ़ंक्शन का उपयोग कर सकते हैं:

 library (moments)

#calculate skewness
skewness(data)

[1] -1.391777

#calculate kurtosis
kurtosis(data)

[1] 4.177865

तिरछापन -1.391777 निकला और कुर्टोसिस 4.177865 निकला।

चूँकि विषमता ऋणात्मक है, यह इंगित करता है कि वितरण विषम रह गया है। यह पुष्टि करता है कि हमने हिस्टोग्राम में क्या देखा।

चूंकि कर्टोसिस 3 से अधिक है, यह इंगित करता है कि वितरण में सामान्य वितरण की तुलना में पूंछ में अधिक मूल्य हैं।

मोमेंट्स लाइब्रेरी Jarque.test() फ़ंक्शन भी प्रदान करती है, जो एक फिट-ऑफ-फिट परीक्षण करता है जो यह निर्धारित करता है कि नमूना डेटा सामान्य वितरण के अनुरूप तिरछापन और कर्टोसिस प्रदर्शित करता है या नहीं। इस परीक्षण की शून्य और वैकल्पिक परिकल्पनाएँ इस प्रकार हैं:

शून्य परिकल्पना : डेटा सेट में तिरछापन और कुर्टोसिस है जो सामान्य वितरण से मेल खाता है।

वैकल्पिक परिकल्पना : डेटासेट में तिरछापन और कुर्टोसिस है जो सामान्य वितरण के अनुरूप नहीं है ।

निम्नलिखित कोड दिखाता है कि यह परीक्षण कैसे करें:

 jarque.test(data)

	Jarque-Bera Normality Test

data:data
JB = 5.7097, p-value = 0.05756
alternative hypothesis: greater

परीक्षण का पी-मान 0.05756 निकला। चूँकि यह मान α = 0.05 से कम नहीं है, हम शून्य परिकल्पना को अस्वीकार करने में विफल हैं। हमारे पास यह कहने के लिए पर्याप्त सबूत नहीं हैं कि इस डेटासेट में सामान्य वितरण से अलग विषमता और कर्टोसिस है।

आप संपूर्ण मोमेंट्स लाइब्रेरी दस्तावेज़ यहां पा सकते हैं।

बोनस: तिरछापन और कर्टोसिस कैलकुलेटर

आप सांख्यिकीय तिरछापन और कर्टोसिस कैलकुलेटर का उपयोग करके किसी दिए गए डेटासेट के लिए तिरछापन की गणना भी कर सकते हैं , जो स्वचालित रूप से किसी दिए गए डेटासेट के लिए तिरछापन और कर्टोसिस की गणना करता है।