आर में वेल्च का टी-टेस्ट कैसे करें

वेल्च के टी-टेस्ट का उपयोग दो स्वतंत्र समूहों के बीच माध्यों की तुलना करने के लिए किया जाता है जब यह नहीं माना जाता है कि दोनों समूहों में समान भिन्नताएं हैं।

R में वेल्च का t-परीक्षण करने के लिए, हम t.test() फ़ंक्शन का उपयोग कर सकते हैं, जो निम्नलिखित सिंटैक्स का उपयोग करता है:

t.परीक्षण(x, y, वैकल्पिक = c(“दो फलक”, “कम”, “अधिक”))

सोना:

• x: पहले समूह के लिए डेटा मानों का एक संख्यात्मक वेक्टर
• y: दूसरे समूह के लिए डेटा मानों का एक संख्यात्मक वेक्टर
• वैकल्पिक: परीक्षण के लिए वैकल्पिक परिकल्पना। डिफ़ॉल्ट दोतरफा है.

निम्नलिखित उदाहरण दिखाता है कि आर में वेल्च का टी-टेस्ट करने के लिए इस फ़ंक्शन का उपयोग कैसे करें।

उदाहरण: आर में वेल्च का टी-टेस्ट

एक शिक्षक उन 12 छात्रों के परीक्षा परिणामों की तुलना करना चाहता है जिन्होंने परीक्षा की तैयारी के लिए परीक्षण तैयारी पुस्तिका का उपयोग किया था और उन 12 छात्रों के परीक्षा परिणामों की तुलना करना चाहते हैं जिन्होंने परीक्षा की तैयारी नहीं की थी।

निम्नलिखित वेक्टर प्रत्येक समूह में छात्रों के परीक्षा परिणाम दिखाते हैं:

 booklet <- c(90, 85, 88, 89, 94, 91, 79, 83, 87, 88, 91, 90)
no_booklet <- c(67, 90, 71, 95, 88, 83, 72, 66, 75, 86, 93, 84)

वेल्च का टी-टेस्ट करने से पहले, हम प्रत्येक समूह के लिए अंकों के वितरण की कल्पना करने के लिए पहले बॉक्सप्लॉट बना सकते हैं:

 boxplot(booklet, no_booklet, names =c(" Booklet "," No Booklet "))

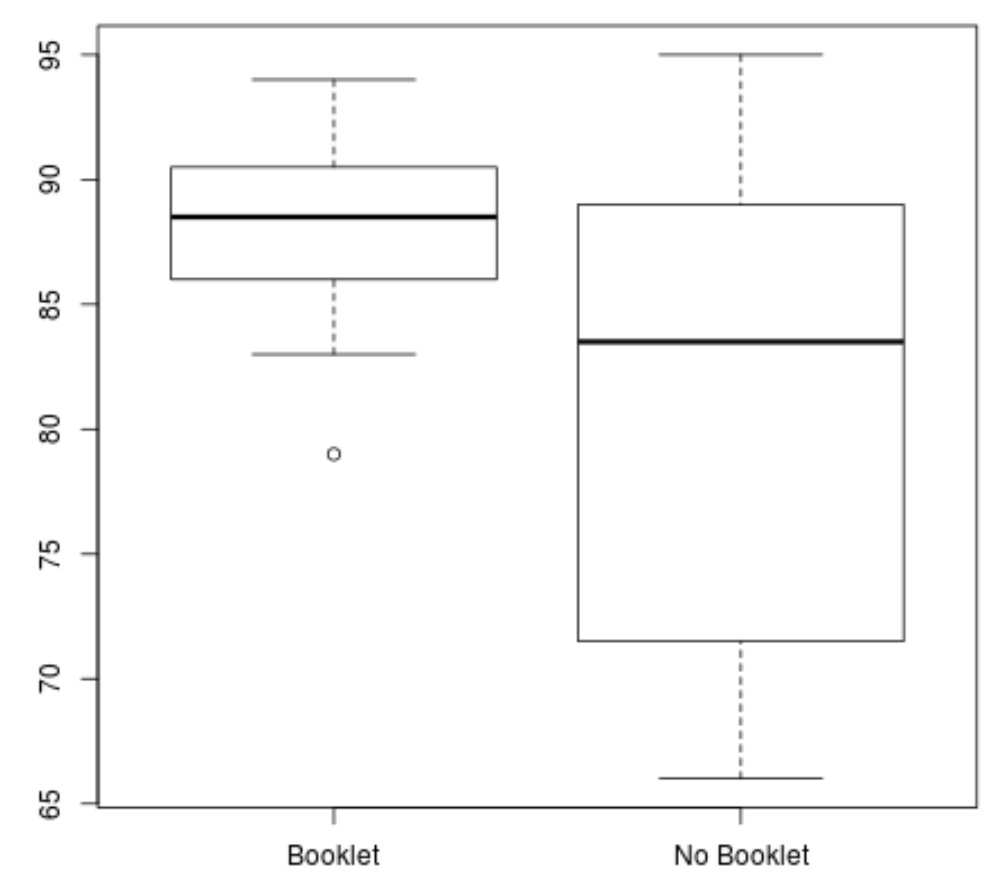
हम स्पष्ट रूप से देख सकते हैं कि “बुकलेट” समूह का औसत स्कोर अधिक है और स्कोर भिन्नता कम है।

औपचारिक रूप से परीक्षण करने के लिए कि क्या समूहों के बीच औसत स्कोर काफी भिन्न हैं, हम वेल्च का टी-टेस्ट कर सकते हैं:

 #perform Welch's t-test
t.test(booklet, no_booklet)

	Welch Two Sample t-test

data: booklet and no_booklet
t = 2.2361, df = 14.354, p-value = 0.04171
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
  0.3048395 13.8618272
sample estimates:
mean of x mean of y 
 87.91667 80.83333 

परिणाम से, हम देख सकते हैं कि टी -टेस्ट आँकड़ा 2.2361 है और संबंधित पी-मान 0.04171 है।

चूँकि यह पी-वैल्यू 0.05 से कम है, हम शून्य परिकल्पना को अस्वीकार कर सकते हैं और निष्कर्ष निकाल सकते हैं कि दोनों समूहों के बीच औसत परीक्षा स्कोर में सांख्यिकीय रूप से महत्वपूर्ण अंतर है।

T.test() फ़ंक्शन हमें निम्नलिखित जानकारी भी प्रदान करता है:

• दोनों समूहों के बीच औसत परीक्षा स्कोर में अंतर के लिए 95% आत्मविश्वास अंतराल [0.3048, 13.8618 ] है।
• पहले समूह का औसत परीक्षा स्कोर 87.91667 है।
• दूसरे समूह का औसत परीक्षा स्कोर 80.83333 है।

आप t.test() फ़ंक्शन के लिए संपूर्ण दस्तावेज़ यहां पा सकते हैं।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल बताते हैं कि आर में अन्य सामान्य कार्य कैसे करें:

आर में एक-नमूना टी-टेस्ट कैसे करें
आर में दो-नमूना टी-परीक्षण कैसे करें
आर में युग्मित नमूने टी-परीक्षण कैसे करें
आर में एक ही ग्राफ़ में एकाधिक बॉक्सप्लॉट कैसे प्लॉट करें