आर में रिज रिग्रेशन (कदम दर कदम)

रिज रिग्रेशन एक ऐसी विधि है जिसका उपयोग हम एक रिग्रेशन मॉडल को फिट करने के लिए कर सकते हैं जब डेटा में मल्टीकॉलिनेरिटी मौजूद होती है।

संक्षेप में, न्यूनतम वर्ग प्रतिगमन उन गुणांक अनुमानों को खोजने का प्रयास करता है जो वर्गों के अवशिष्ट योग (आरएसएस) को कम करते हैं:

RSS = Σ(y _i – ŷ _i )2

सोना:

• Σ : एक ग्रीक प्रतीक जिसका अर्थ है योग
• y _i : ^iवें अवलोकन के लिए वास्तविक प्रतिक्रिया मान
• ŷ _i : एकाधिक रेखीय प्रतिगमन मॉडल के आधार पर अनुमानित प्रतिक्रिया मूल्य

इसके विपरीत, रिज प्रतिगमन निम्नलिखित को कम करने का प्रयास करता है:

आरएसएस + λΣβ _जे ²

जहां j 1 से p भविष्यवक्ता चर और λ ≥ 0 तक जाता है।

समीकरण में इस दूसरे पद को निकासी दंड के रूप में जाना जाता है। रिज रिग्रेशन में, हम λ के लिए एक मान का चयन करते हैं जो न्यूनतम संभव एमएसई परीक्षण (माध्य वर्ग त्रुटि) उत्पन्न करता है।

यह ट्यूटोरियल आर में रिज रिग्रेशन कैसे करें इसका चरण-दर-चरण उदाहरण प्रदान करता है।

चरण 1: डेटा लोड करें

इस उदाहरण के लिए, हम R के अंतर्निहित डेटासेट का उपयोग करेंगे जिसे mtcars कहा जाता है। हम एचपी को प्रतिक्रिया चर के रूप में और निम्नलिखित चर को भविष्यवक्ता के रूप में उपयोग करेंगे:

• एमपीजी
• वज़न
• मल
• क्यूसेक

रिज रिग्रेशन करने के लिए, हम glmnet पैकेज से फ़ंक्शंस का उपयोग करेंगे। इस पैकेज के लिए आवश्यक है कि प्रतिक्रिया चर एक वेक्टर हो और भविष्यवक्ता चर का सेट data.matrix वर्ग का हो।

निम्नलिखित कोड दिखाता है कि हमारे डेटा को कैसे परिभाषित किया जाए:

 #define response variable
y <- mtcars$hp

#define matrix of predictor variables
x <- data.matrix(mtcars[, c('mpg', 'wt', 'drat', 'qsec')])

चरण 2: रिज रिग्रेशन मॉडल को फिट करें

इसके बाद, हम रिज रिग्रेशन मॉडल को फिट करने और alpha=0 निर्दिष्ट करने के लिए glmnet() फ़ंक्शन का उपयोग करेंगे।

ध्यान दें कि अल्फा को 1 के बराबर सेट करना लैस्सो रिग्रेशन का उपयोग करने के बराबर है और अल्फा को 0 और 1 के बीच के मान पर सेट करना एक इलास्टिक नेट का उपयोग करने के बराबर है।

यह भी ध्यान दें कि रिज रिग्रेशन के लिए डेटा को इस तरह मानकीकृत करने की आवश्यकता होती है कि प्रत्येक भविष्यवक्ता चर का माध्य 0 और मानक विचलन 1 हो।

सौभाग्य से, glmnet() स्वचालित रूप से आपके लिए यह मानकीकरण करता है। यदि आपने पहले से ही चर को मानकीकृत कर लिया है, तो आप मानकीकृत = गलत निर्दिष्ट कर सकते हैं।

 library (glmnet)

#fit ridge regression model
model <- glmnet(x, y, alpha = 0 )

#view summary of model
summary(model)

          Length Class Mode   
a0 100 -none- numeric
beta 400 dgCMatrix S4     
df 100 -none- numeric
dim 2 -none- numeric
lambda 100 -none- numeric
dev.ratio 100 -none- numeric
nulldev 1 -none- numeric
npasses 1 -none- numeric
jerr 1 -none- numeric
offset 1 -none- logical
call 4 -none- call   
nobs 1 -none- numeric

चरण 3: लैम्ब्डा के लिए एक इष्टतम मान चुनें

इसके बाद, हम लैम्ब्डा मान की पहचान करेंगे जो के-फोल्ड क्रॉस-वैलिडेशन का उपयोग करके सबसे कम परीक्षण माध्य वर्ग त्रुटि (एमएसई) उत्पन्न करता है।

सौभाग्य से, glmnet में cv.glmnet() फ़ंक्शन है जो k = 10 बार का उपयोग करके स्वचालित रूप से k-फोल्ड क्रॉस-सत्यापन करता है।

 #perform k-fold cross-validation to find optimal lambda value
cv_model <- cv. glmnet (x, y, alpha = 0 )

#find optimal lambda value that minimizes test MSE
best_lambda <- cv_model$ lambda . min
best_lambda

[1] 10.04567

#produce plot of test MSE by lambda value
plot(cv_model) 

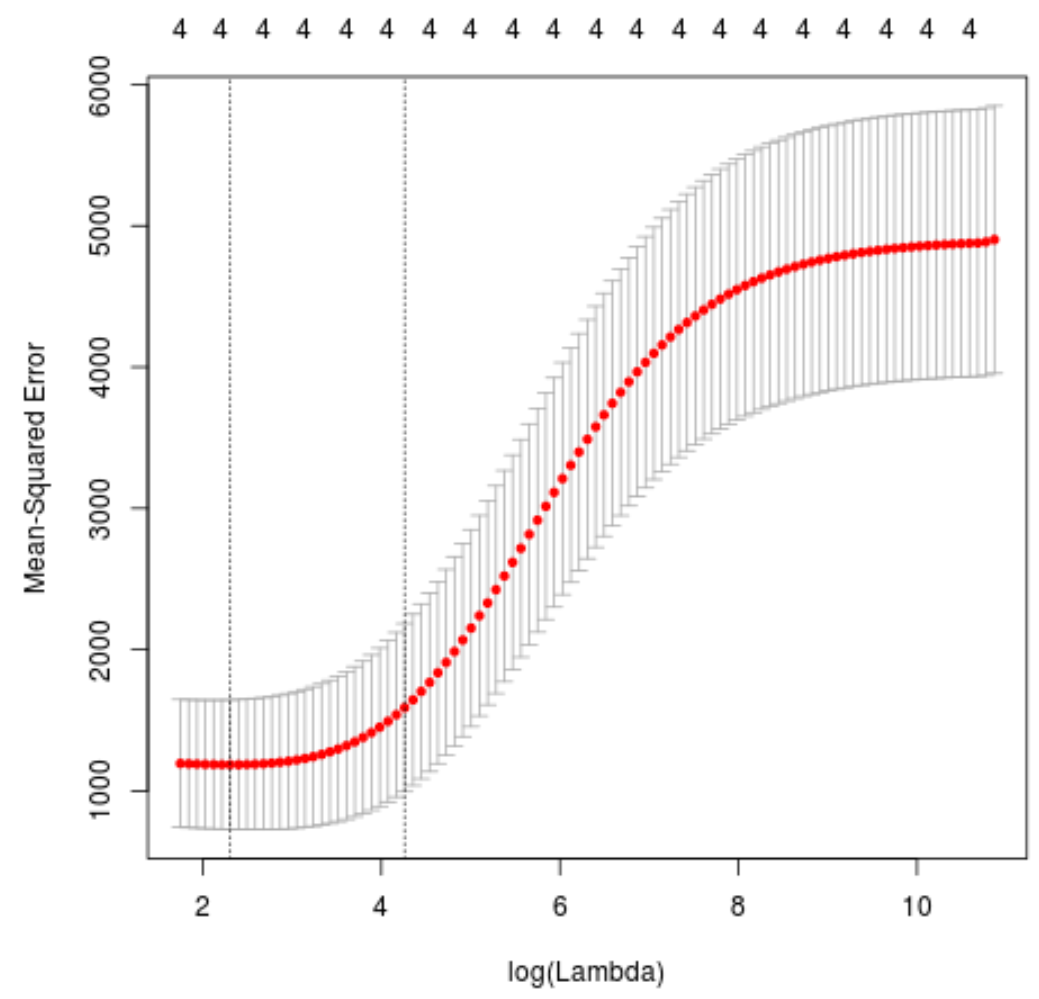
एमएसई परीक्षण को न्यूनतम करने वाला लैम्ब्डा मान 10.04567 निकला।

चरण 4: अंतिम मॉडल का विश्लेषण करें

अंत में, हम इष्टतम लैम्ब्डा मान द्वारा निर्मित अंतिम मॉडल का विश्लेषण कर सकते हैं।

इस मॉडल के लिए गुणांक अनुमान प्राप्त करने के लिए हम निम्नलिखित कोड का उपयोग कर सकते हैं:

 #find coefficients of best model
best_model <- glmnet(x, y, alpha = 0 , lambda = best_lambda)
coef(best_model)

5 x 1 sparse Matrix of class "dgCMatrix"
                    s0
(Intercept) 475.242646
mpg -3.299732
wt 19.431238
drat -1.222429
qsec -17.949721

हम यह देखने के लिए एक ट्रेस प्लॉट भी तैयार कर सकते हैं कि लैम्ब्डा में वृद्धि के कारण गुणांक अनुमान कैसे बदल गए हैं:

 #produce Ridge trace plot
plot(model, xvar = " lambda ") 

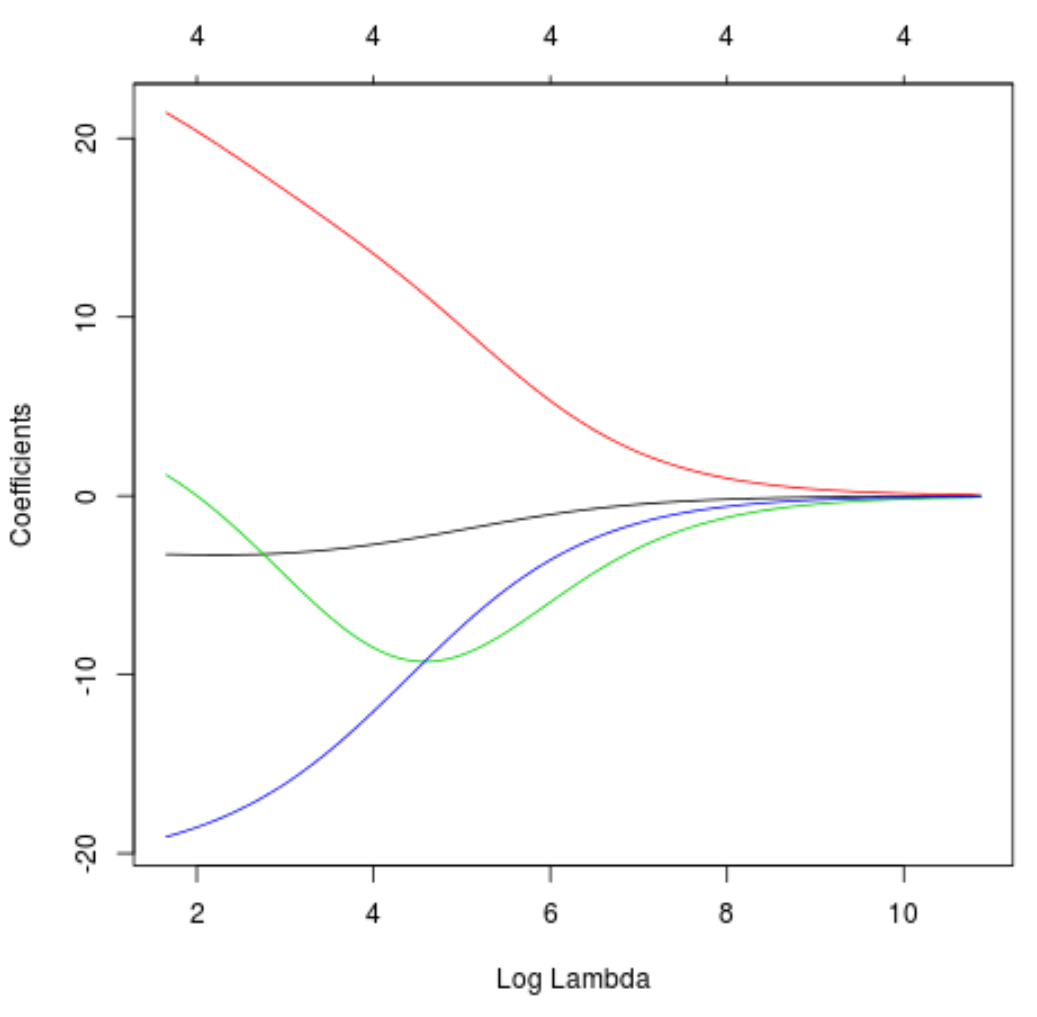
अंत में, हम प्रशिक्षण डेटा पर मॉडल के आर-वर्ग की गणना कर सकते हैं:

 #use fitted best model to make predictions
y_predicted <- predict (model, s = best_lambda, newx = x)

#find OHS and SSE
sst <- sum ((y - mean (y))^2)
sse <- sum ((y_predicted - y)^2)

#find R-Squared
rsq <- 1 - sse/sst
rsq

[1] 0.7999513

R वर्ग 0.7999513 निकला। यानी, सबसे अच्छा मॉडल प्रशिक्षण डेटा के प्रतिक्रिया मूल्यों में 79.99% भिन्नता को समझाने में सक्षम था।

आप इस उदाहरण में प्रयुक्त पूरा आर कोड यहां पा सकते हैं।