आवृति वितरण
यह आलेख बताता है कि आवृत्ति वितरण क्या हैं और उन्हें कैसे प्राप्त किया जाता है। आपको आवृत्ति वितरण के चरण-दर-चरण उदाहरण भी मिलेंगे और इसके अलावा, आप हल किए गए अभ्यासों का अभ्यास करने में सक्षम होंगे।
आवृत्ति वितरण क्या है?
आँकड़ों में, आवृत्ति वितरण एक तालिका है जिसमें किसी नमूने के विभिन्न मानों को पंक्तियों में समूहीकृत किया जाता है और प्रत्येक कॉलम में प्रत्येक मान का एक आवृत्ति प्रकार प्रदर्शित किया जाता है। इसलिए, डेटा सेट में सभी प्रकार की आवृत्तियों को दिखाने के लिए आवृत्ति वितरण का उपयोग किया जाता है।
अधिक विशेष रूप से, एक आवृत्ति वितरण में पूर्ण आवृत्ति, संचयी पूर्ण आवृत्ति, सापेक्ष आवृत्ति और संचयी सापेक्ष आवृत्ति शामिल होती है।
आवृत्ति वितरण की एक विशेषता यह है कि वे मात्रात्मक चर और गुणात्मक चर के सांख्यिकीय नमूने को सारांशित करने के लिए बहुत उपयोगी होते हैं।
आवृत्ति वितरण कैसे करें
आवृत्ति वितरण करने के लिए, आपको निम्नलिखित चरणों का पालन करना होगा:
- डेटा को विभिन्न श्रेणियों में व्यवस्थित करें और एक तालिका बनाएं जिसमें प्रत्येक पंक्ति एक श्रेणी से मेल खाती हो।
- तालिका के दूसरे कॉलम में प्रत्येक श्रेणी की पूर्ण आवृत्ति की गणना करें।
- तालिका के तीसरे कॉलम में प्रत्येक श्रेणी की संचयी निरपेक्ष आवृत्ति की गणना करें।
- तालिका के चौथे कॉलम में प्रत्येक श्रेणी की सापेक्ष आवृत्ति की गणना करें।
- तालिका के पांचवें कॉलम में प्रत्येक श्रेणी की संचयी सापेक्ष आवृत्ति की गणना करें।
- वैकल्पिक रूप से, दो कॉलम जोड़े जा सकते हैं जिनमें सापेक्ष आवृत्ति और संचयी सापेक्ष आवृत्ति की गणना प्रतिशत के रूप में की जाती है, इसके लिए आपको बस दोनों कॉलमों को 100 से गुणा करना होगा।
आवृत्ति वितरण का उदाहरण
एक बार जब हमने आवृत्ति वितरण की परिभाषा और इसके निर्माण के सिद्धांत को देख लिया है, तो इस खंड में एक उदाहरण को चरण दर चरण हल किया गया है।
- 30 छात्रों की एक कक्षा में सांख्यिकी विषय में प्राप्त ग्रेड इस प्रकार हैं। डेटासेट का आवृत्ति वितरण बनाएं।
![]()
![]()
![]()
चूँकि सभी संख्याएँ केवल पूर्णांक हो सकती हैं, यह एक असतत चर है। इसलिए डेटा को अंतरालों में समूहित करना आवश्यक नहीं है।
इसलिए, आवृत्ति वितरण बनाने के लिए, हमें एक तालिका बनाने की आवश्यकता है जिसमें प्रत्येक भिन्न मान एक पंक्ति होगी, और फिर हमें प्रत्येक मान की पूर्ण आवृत्ति ज्ञात करने की आवश्यकता है:

ध्यान दें कि सभी निरपेक्ष आवृत्तियों का योग डेटा की कुल संख्या के बराबर है। यदि इस नियम का सम्मान नहीं किया जाता है, तो इसका मतलब है कि आप कुछ जानकारी प्रदान करना भूल गए हैं।
अब जब हम निरपेक्ष आवृत्ति जानते हैं, तो हमें संचयी निरपेक्ष आवृत्ति की गणना करने की आवश्यकता है। इस गणना के लिए हमारे पास दो विकल्प हैं: या तो हम मूल्य की पूर्ण आवृत्ति और सबसे छोटे मूल्यों की सभी पूर्ण आवृत्तियों को जोड़ दें, या इसके विपरीत, हम मूल्य की पूर्ण आवृत्ति और पिछले मूल्य की संचयी पूर्ण आवृत्ति को जोड़ दें।

अंतिम मान की संचयी निरपेक्ष आवृत्ति हमेशा डेटा की कुल संख्या से मेल खाती है, आप यह सत्यापित करने के लिए इस ट्रिक का उपयोग कर सकते हैं कि गणना सही है।
इसके बाद, हमें सापेक्ष आवृत्ति निर्धारित करने की आवश्यकता है, जिसकी गणना पूर्ण आवृत्ति को डेटा बिंदुओं की कुल संख्या (30) से विभाजित करके की जाती है:

ध्यान रखें कि सभी सापेक्ष आवृत्तियों का योग हमेशा 1 के बराबर होता है, अन्यथा इसका मतलब है कि आवृत्ति वितरण की एक निश्चित गणना गलत है।
अंत में, हमें केवल संचयी सापेक्ष आवृत्ति निकालने की आवश्यकता है। ऐसा करने के लिए, आपको प्रश्न में मूल्य की सापेक्ष आवृत्ति और पिछली सभी सापेक्ष आवृत्तियों को जोड़ना होगा या, जो एक ही चीज़ के बराबर है, पिछली संचित सापेक्ष आवृत्ति:

संक्षेप में, समस्या डेटा की सभी आवृत्तियों के साथ आवृत्ति वितरण इस प्रकार है:

समूहीकृत डेटा के लिए आवृत्ति वितरण
अंतरालों में समूहित डेटा के लिए आवृत्ति वितरण करने के लिए, एकमात्र अंतर यह है कि डेटा सेट को पहले अलग-अलग अंतरालों में समूहीकृत किया जाना चाहिए, लेकिन बाकी गणना उसी तरह की जाती है जैसे आवृत्ति वितरण में डेटा को समूहीकृत किए बिना किया जाता है।
उदाहरण के तौर पर, समूहीकृत डेटा के लिए आवृत्ति वितरण के निर्माण की समस्या को नीचे हल किया गया है।
- 20 लोगों की ऊंचाई मापी गई और नीचे दिए गए परिणाम प्राप्त किए गए। डेटा को अंतरालों में अलग करके एक आवृत्ति वितरण बनाएं।
![]()
![]()
इस नमूने में डेटा एक सतत वितरण का अनुसरण करता है, क्योंकि संख्याएँ दशमलव हो सकती हैं और इसलिए कोई भी मान ले सकती हैं। इसलिए, हम डेटा को अंतरालों में समूहित करके आवृत्ति वितरण बनाएंगे।
हालाँकि किसी नमूने के अंतराल बनाने के लिए कई गणितीय नियम हैं, इस मामले में हम केवल 10 दसवें की चौड़ाई के साथ अंतराल बनाएंगे।
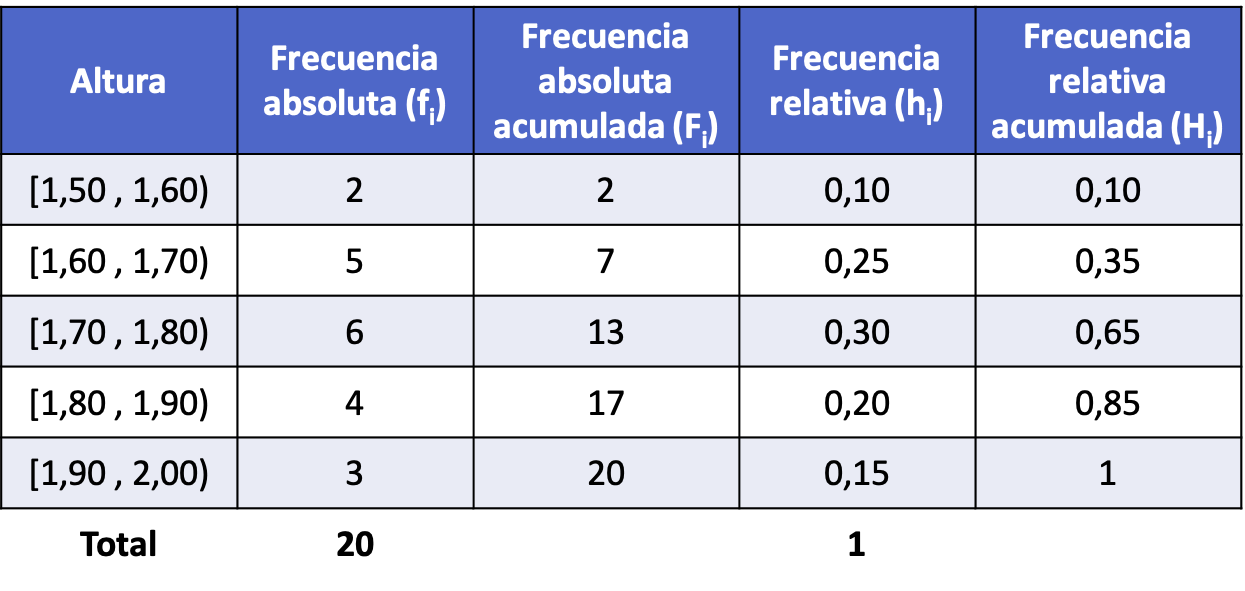
इसलिए, प्रत्येक अंतराल के लिए सभी आवृत्ति प्रकारों की गणना करने के बाद (प्रक्रिया उपरोक्त उदाहरण के समान है), अंतराल में समूहीकृत डेटा के साथ आवृत्ति वितरण इस प्रकार है:
बारंबारता वितरण अभ्यास हल किया गया
अभ्यास 1
हमने 20 लोगों से पूछा कि वे प्रति माह कितनी बार सिनेमा जाते हैं और परिणाम यहां हैं:
![]()
![]()
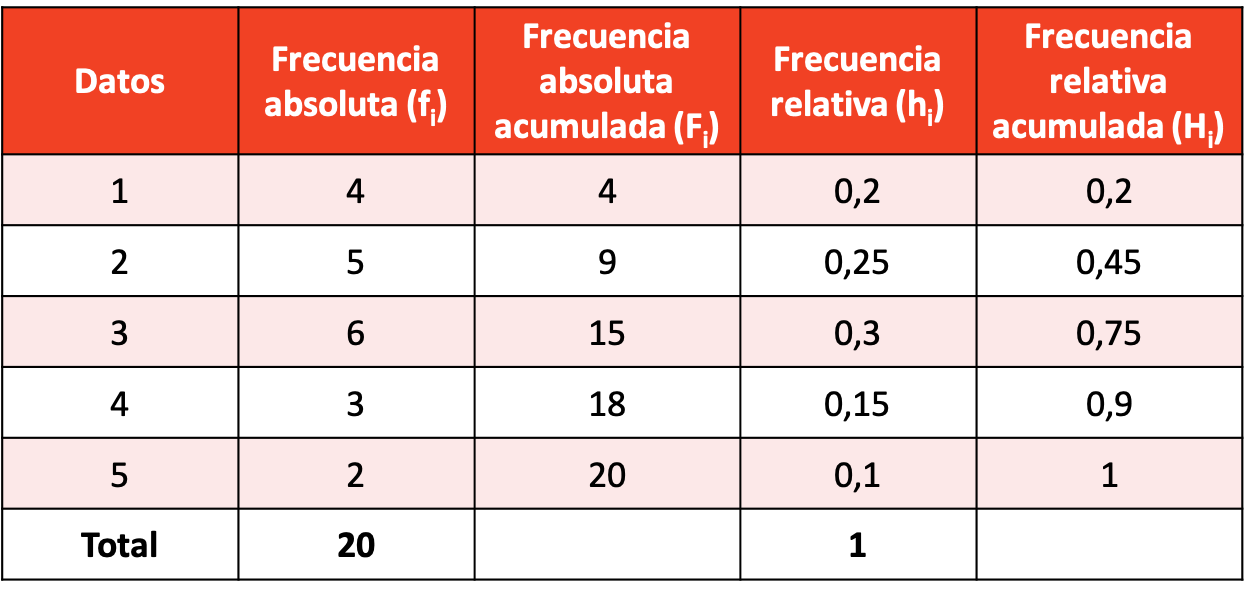
परिणामी डेटा नमूने के साथ एक आवृत्ति वितरण बनाएं।
सभी प्रकार की आवृत्तियों की गणना के साथ आवृत्ति वितरण इस प्रकार है:
व्यायाम 2
आप 36 कर्मचारियों वाली कंपनी में श्रमिकों के वजन पर एक सांख्यिकीय अध्ययन करना चाहेंगे। यहां श्रमिकों का वजन किलोग्राम में व्यक्त किया गया है:
![]()
![]()
![]()
![]()
![]()
![]()
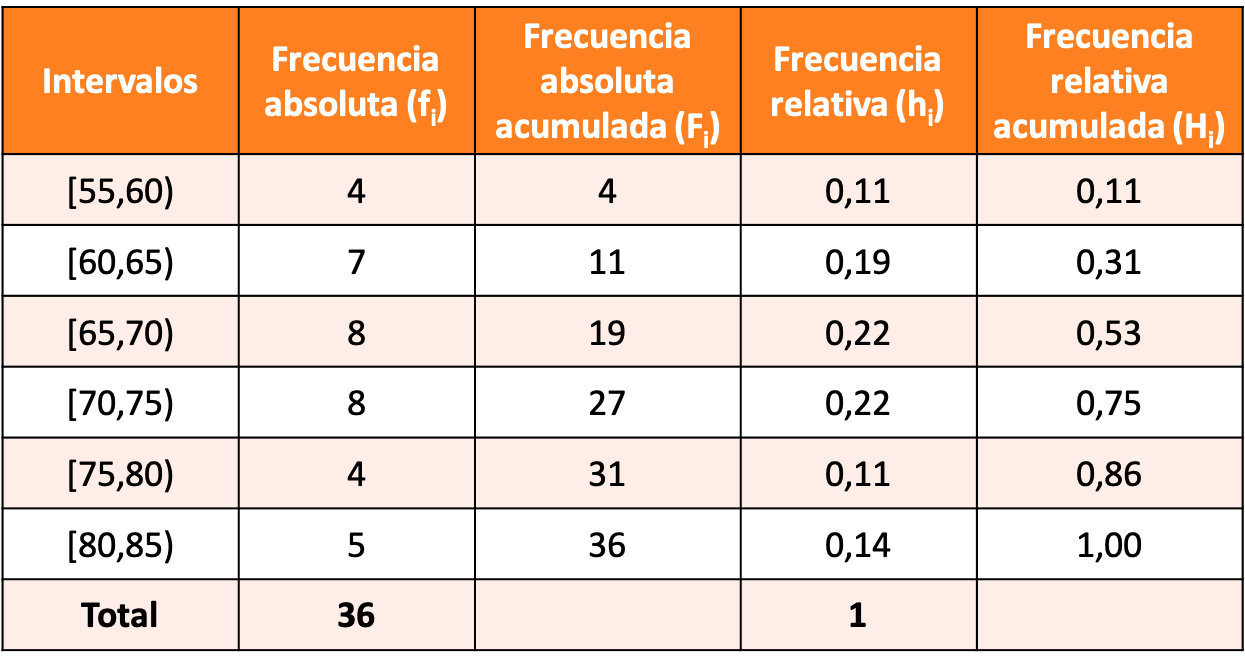
5 इकाइयों का अंतराल बनाकर समूहीकृत डेटा के साथ एक आवृत्ति वितरण का निर्माण करें और पहला अंतराल [55,60) होने दें।
अभ्यास का समाधान निम्नलिखित आवृत्ति वितरण है: