एक्सेल: एकाधिक रैखिक प्रतिगमन करने के लिए linest का उपयोग कैसे करें

आप एकाधिक रैखिक प्रतिगमन मॉडल को डेटा के एक सेट में फिट करने के लिए Excel में LINEST फ़ंक्शन का उपयोग कर सकते हैं।

यह फ़ंक्शन निम्नलिखित मूल सिंटैक्स का उपयोग करता है:

 = LINEST ( known_y's, [known_x's], [const], [stats] )

सोना:

• Known_y’s : ज्ञात y मानों की एक सारणी
• ज्ञात_x : ज्ञात x मानों की एक सरणी
• स्थिरांक : वैकल्पिक तर्क. यदि सत्य है, तो स्थिरांक b को सामान्य रूप से संसाधित किया जाता है। यदि गलत है, तो स्थिरांक b को 1 पर सेट किया गया है।
• आँकड़े : वैकल्पिक तर्क. यदि सत्य है, तो अतिरिक्त प्रतिगमन आँकड़े लौटाए जाते हैं। यदि गलत है, तो अतिरिक्त प्रतिगमन आँकड़े वापस नहीं किए जाते हैं।

निम्नलिखित चरण-दर-चरण उदाहरण दिखाता है कि व्यवहार में इस फ़ंक्शन का उपयोग कैसे करें।

चरण 1: डेटा दर्ज करें

सबसे पहले, आइए एक्सेल में निम्नलिखित डेटा सेट दर्ज करें:

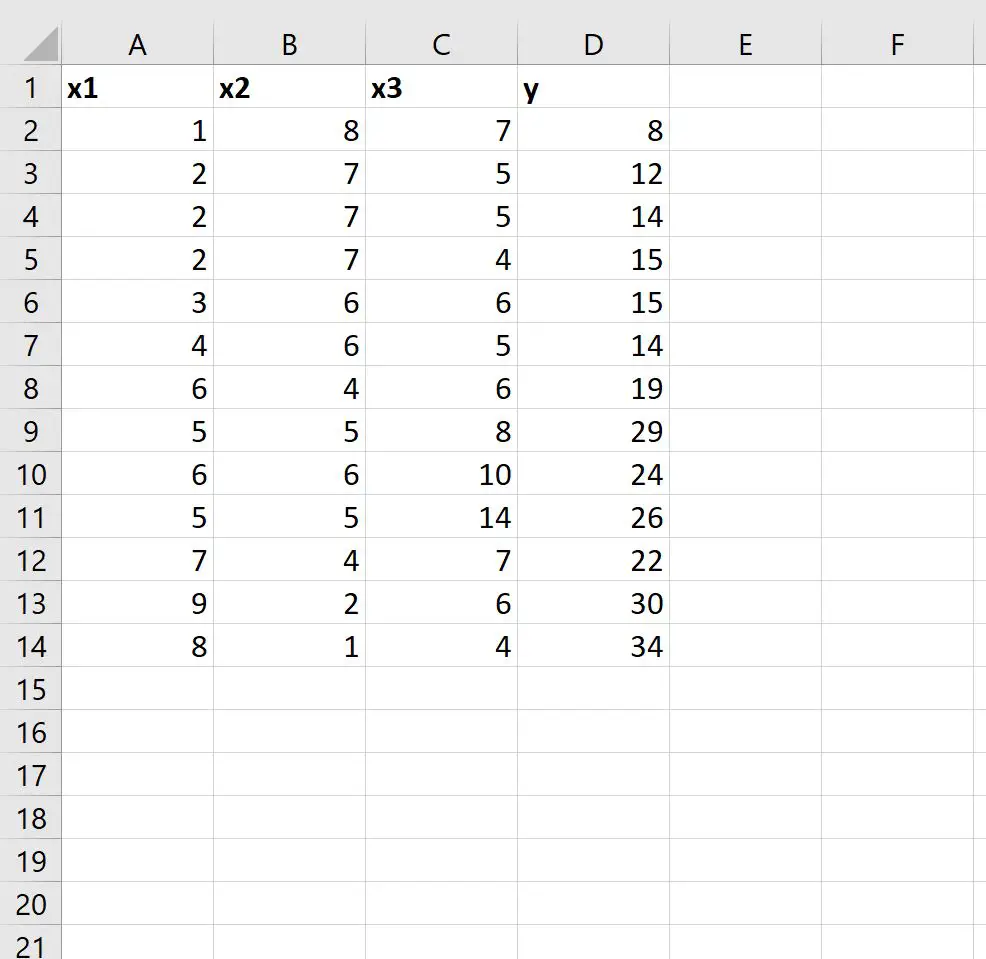
चरण 2: एकाधिक रैखिक प्रतिगमन मॉडल को फिट करने के लिए LINEST का उपयोग करें

मान लीजिए कि हम भविष्यवक्ता चर के रूप में x1 , x2 , और x3 और प्रतिक्रिया चर के रूप में y का उपयोग करके एक एकाधिक रैखिक प्रतिगमन मॉडल फिट करना चाहते हैं।

ऐसा करने के लिए, हम इस एकाधिक रैखिक प्रतिगमन मॉडल को फिट करने के लिए किसी भी सेल में निम्नलिखित सूत्र टाइप कर सकते हैं

 =LINEST( D2:D14 , A2:C14 )

निम्नलिखित स्क्रीनशॉट दिखाता है कि व्यवहार में इस सूत्र का उपयोग कैसे करें:

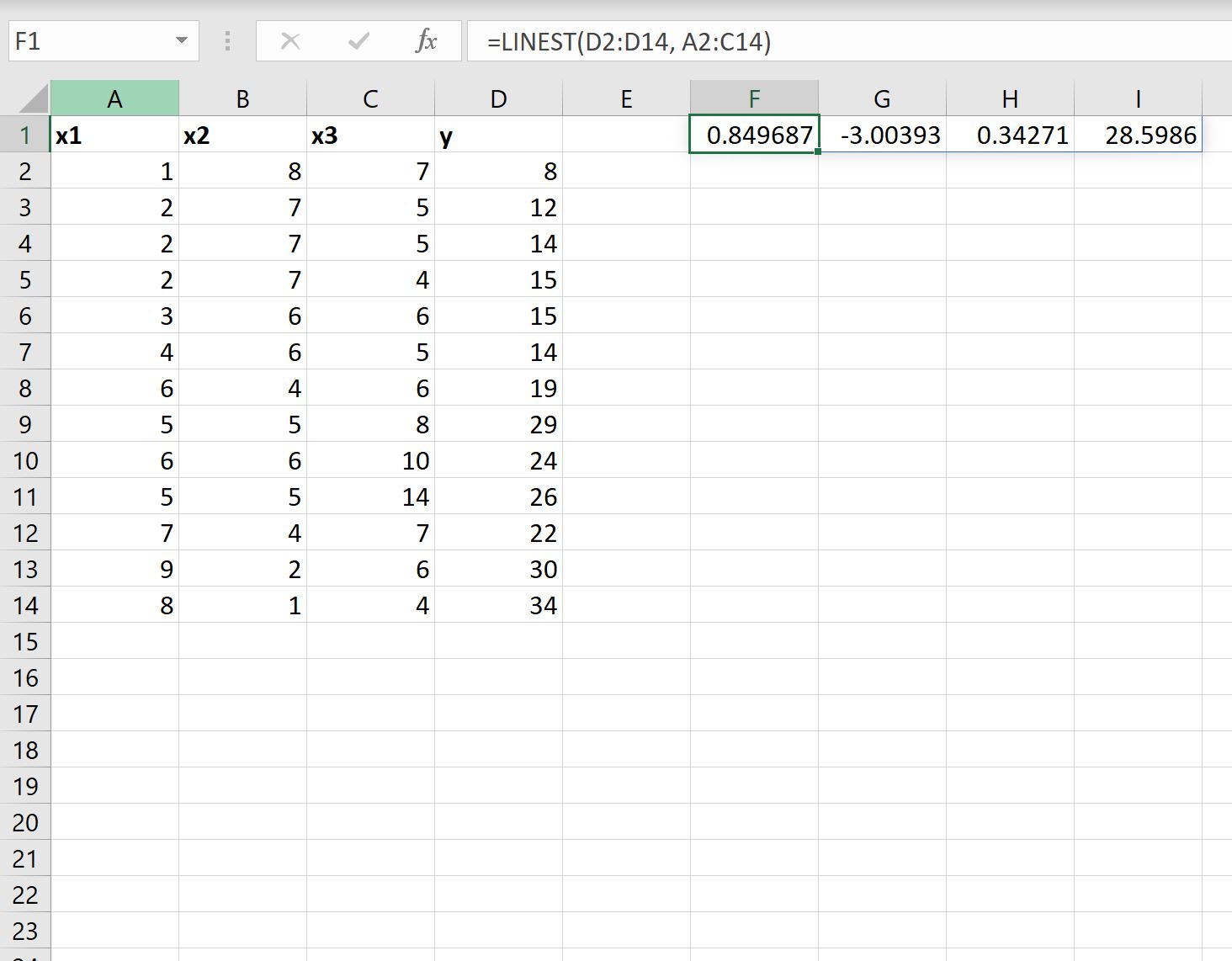
यहां परिणाम की व्याख्या करने का तरीका बताया गया है:

• अवरोधन का गुणांक 28.5986 है।
• X1 का गुणांक 0.34271 है।
• x2 का गुणांक -3.00393 है।
• x3 का गुणांक 0.849687 है।

इन गुणांकों का उपयोग करके, हम फिट किए गए प्रतिगमन समीकरण को निम्नानुसार लिख सकते हैं:

y = 28.5986 + 0.34271(x1) – 3.00393(x2) + 0.849687(x3)

चरण 3 (वैकल्पिक): अतिरिक्त प्रतिगमन आँकड़े देखें

फिट किए गए प्रतिगमन समीकरण के लिए अतिरिक्त प्रतिगमन आँकड़े प्रदर्शित करने के लिए हम LINEST फ़ंक्शन में आँकड़े तर्क का मान TRUE के बराबर भी सेट कर सकते हैं:

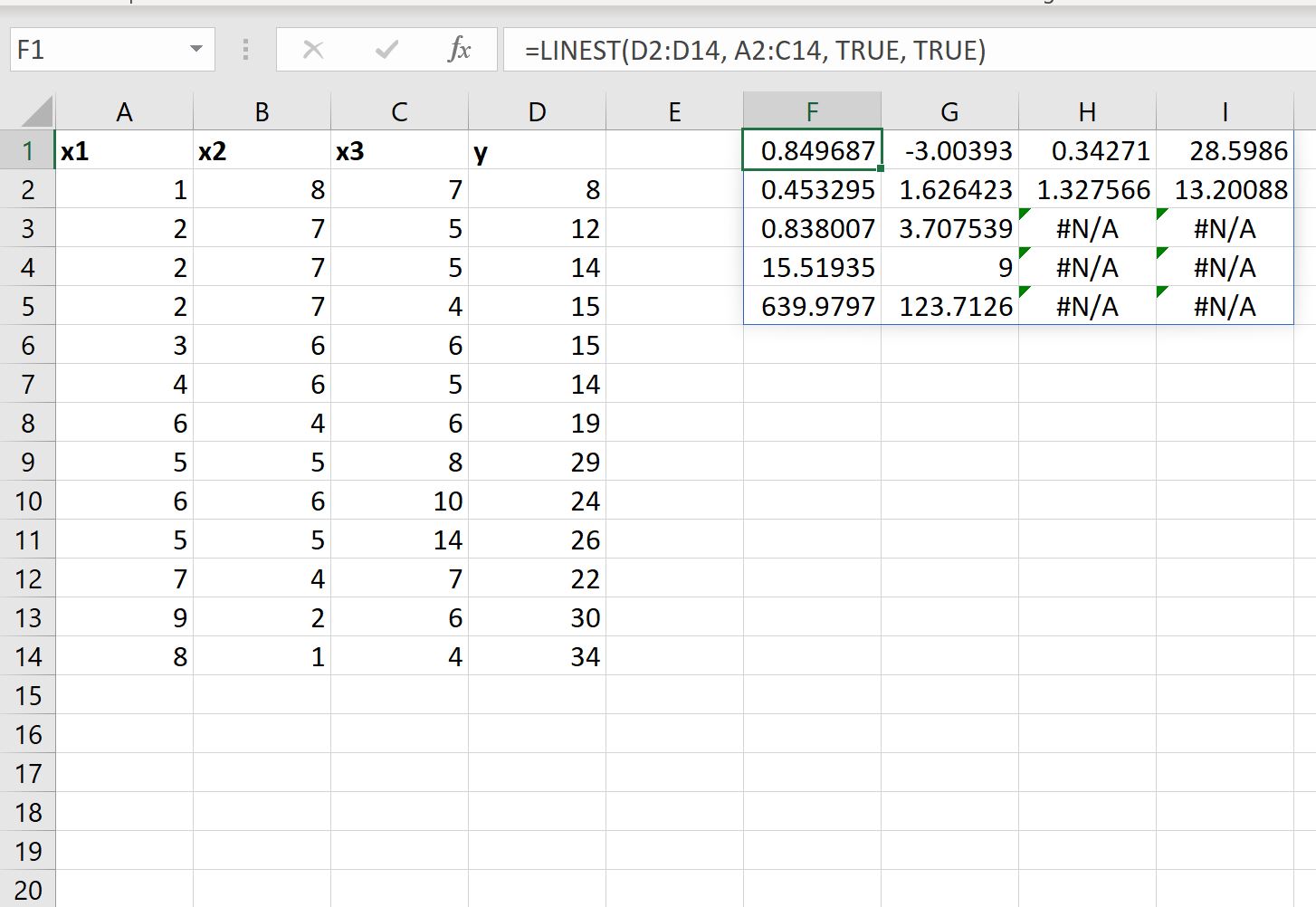
फिट किया गया प्रतिगमन समीकरण अभी भी वही है:

y = 28.5986 + 0.34271(x1) – 3.00393(x2) + 0.849687(x3)

यहां परिणाम के अन्य मूल्यों की व्याख्या करने का तरीका बताया गया है:

• x3 के लिए मानक त्रुटि 0.453295 है।
• x2 के लिए मानक त्रुटि 1.626423 है।
• X1 के लिए मानक त्रुटि 1.327566 है।
• अवरोधन के लिए मानक त्रुटि 13.20088 है।
• मॉडल का R ² .838007 है।
• y के लिए अवशिष्ट मानक त्रुटि 3.707539 है।
• समग्र एफ आँकड़ा 15.51925 है।
• स्वतंत्रता की कोटियाँ 9 हैं।
• वर्गों का प्रतिगमन योग 639.9797 है।
• वर्गों का शेष योग 123.7126 है।

सामान्य तौर पर, इन अतिरिक्त आँकड़ों में सबसे अधिक रुचि का माप आर ² मान है, जो प्रतिक्रिया चर में भिन्नता के अनुपात का प्रतिनिधित्व करता है जिसे भविष्यवक्ता चर द्वारा समझाया जा सकता है।

R ² का मान 0 से 1 तक भिन्न हो सकता है।

चूँकि इस विशेष मॉडल का R ² 0.838 है, यह हमें बताता है कि भविष्यवक्ता चर प्रतिक्रिया चर y के मूल्य की भविष्यवाणी करने का अच्छा काम कर रहे हैं।

संबंधित: एक अच्छा आर-वर्ग मान क्या है?

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल बताते हैं कि एक्सेल में अन्य सामान्य ऑपरेशन कैसे करें:

Excel में LOGEST फ़ंक्शन का उपयोग कैसे करें
एक्सेल में नॉनलीनियर रिग्रेशन कैसे करें
एक्सेल में क्यूबिक रिग्रेशन कैसे करें