एनोवा मॉडल के लिए शून्य परिकल्पना को समझना

एक-तरफ़ा एनोवा का उपयोग यह निर्धारित करने के लिए किया जाता है कि तीन या अधिक स्वतंत्र समूहों के साधनों के बीच सांख्यिकीय रूप से महत्वपूर्ण अंतर है या नहीं।

एक-तरफ़ा एनोवा निम्नलिखित शून्य और वैकल्पिक परिकल्पनाओं का उपयोग करता है:

• एच ₀ : μ ₁ = μ ₂ = μ ₃ = … = μ _k (सभी समूह साधन समान हैं)
• एच _ए : कम से कम एक समूह का औसत अलग है   आराम

यह तय करने के लिए कि हमें शून्य परिकल्पना को अस्वीकार करना चाहिए या नहीं, हमें एनोवा तालिका परिणाम में पी-मान को संदर्भित करने की आवश्यकता है।

यदि पी-मान महत्व के एक निश्चित स्तर (जैसे 0.05) से नीचे है, तो हम शून्य परिकल्पना को अस्वीकार कर सकते हैं और निष्कर्ष निकाल सकते हैं कि सभी समूह साधन समान नहीं हैं।

दो-तरफा एनोवा का उपयोग यह निर्धारित करने के लिए किया जाता है कि तीन या अधिक स्वतंत्र समूहों के साधनों के बीच सांख्यिकीय रूप से महत्वपूर्ण अंतर है या नहीं, जिन्हें दो चर (कभी-कभी “कारक” भी कहा जाता है) को सौंपा गया है।

दो-तरफा एनोवा एक ही समय में तीन शून्य परिकल्पनाओं का परीक्षण करता है:

• पहले चर के प्रत्येक स्तर पर सभी समूह साधन समान हैं
• दूसरे चर के प्रत्येक स्तर पर सभी समूह साधन समान हैं
• दोनों चरों के बीच कोई अन्योन्यक्रिया प्रभाव नहीं है

यह तय करने के लिए कि हमें प्रत्येक अशक्त परिकल्पना को अस्वीकार करना चाहिए या नहीं, हमें दो-तरफा एनोवा तालिका के परिणाम में पी-मानों को संदर्भित करने की आवश्यकता है।

निम्नलिखित उदाहरण दिखाते हैं कि कैसे निर्णय लिया जाए कि एक-तरफ़ा एनोवा और दो-तरफ़ा एनोवा में शून्य परिकल्पना को अस्वीकार किया जाए या नहीं।

उदाहरण 1: वन-वे एनोवा

मान लीजिए कि हम जानना चाहते हैं कि क्या तीन अलग-अलग परीक्षण तैयारी कार्यक्रमों से किसी दी गई परीक्षा में अलग-अलग औसत अंक प्राप्त होते हैं या नहीं। इसका परीक्षण करने के लिए, हम एक अध्ययन में भाग लेने के लिए 30 छात्रों को भर्ती करते हैं और उन्हें तीन समूहों में विभाजित करते हैं।

प्रत्येक समूह में छात्रों को एक परीक्षा की तैयारी के लिए अगले तीन हफ्तों के लिए तीन परीक्षण तैयारी कार्यक्रमों में से एक का उपयोग करने के लिए यादृच्छिक रूप से सौंपा गया है। तीन सप्ताह के अंत में, सभी छात्र एक ही परीक्षा देते हैं।

प्रत्येक समूह के परीक्षा परिणाम नीचे दिखाए गए हैं:

जब हम इन मानों को वन-वे एनोवा कैलकुलेटर में दर्ज करते हैं, तो हमें आउटपुट के रूप में निम्नलिखित एनोवा तालिका प्राप्त होती है:

ध्यान दें कि पी-वैल्यू 0.11385 है।

इस विशेष उदाहरण के लिए, हम निम्नलिखित शून्य और वैकल्पिक परिकल्पनाओं का उपयोग करेंगे:

• एच ₀ : μ ₁ = μ ₂ = μ ₃ (प्रत्येक समूह के लिए औसत परीक्षा स्कोर बराबर है)
• एच _ए : कम से कम एक समूह का औसत अलग है   आराम

चूँकि एनोवा तालिका का पी-मान 0.05 से कम नहीं है, हम शून्य परिकल्पना को अस्वीकार करने में विफल रहते हैं।

इसका मतलब यह है कि हमारे पास यह कहने के लिए पर्याप्त सबूत नहीं हैं कि तीनों समूहों के औसत परीक्षा अंकों के बीच सांख्यिकीय रूप से महत्वपूर्ण अंतर है।

उदाहरण 2: दोतरफा एनोवा

मान लीजिए कि एक वनस्पतिशास्त्री यह जानना चाहता है कि क्या पौधे की वृद्धि सूर्य के प्रकाश के संपर्क और पानी देने की आवृत्ति से प्रभावित होती है।

वह 40 बीज लगाती है और उन्हें सूरज के संपर्क और पानी देने की आवृत्ति की विभिन्न स्थितियों में दो महीने तक बढ़ने देती है। दो महीने के बाद, वह प्रत्येक पौधे की ऊंचाई दर्ज करती है। परिणाम नीचे दर्शाए गए है:

ऊपर दी गई तालिका में हम देखते हैं कि प्रत्येक परिस्थिति में पाँच पौधे उगाए गए।

उदाहरण के लिए, पांच पौधे दैनिक पानी और बिना धूप के उगाए गए और दो महीने के बाद उनकी ऊंचाई 4.8 इंच, 4.4 इंच, 3.2 इंच, 3.9 इंच और 4.4 इंच थी:

वह एक्सेल में दो-तरफा एनोवा निष्पादित करती है और निम्नलिखित परिणाम प्राप्त करती है:

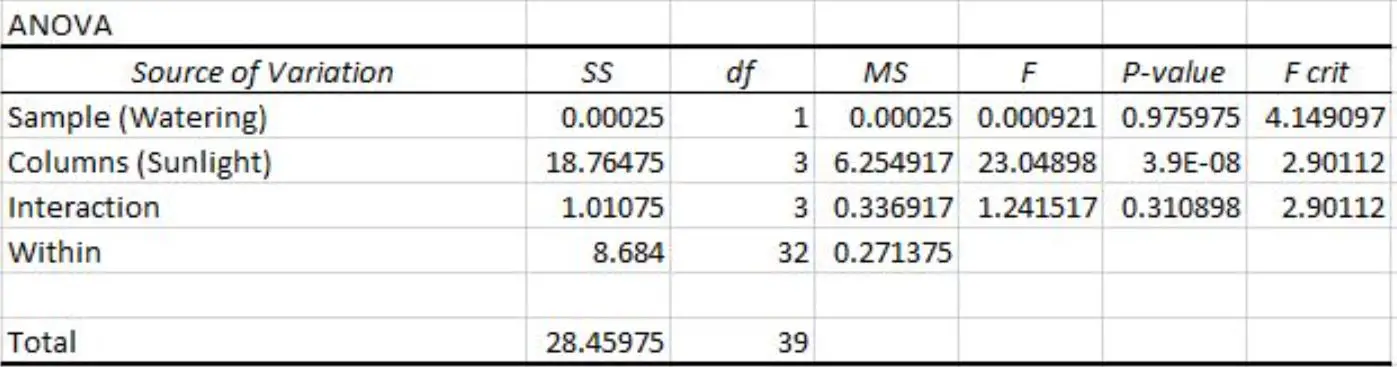
हम दो-तरफा एनोवा तालिका परिणाम में निम्नलिखित पी-मान देख सकते हैं:

• पानी देने की आवृत्ति के लिए पी-मान 0.975975 है। यह 0.05 महत्व स्तर पर सांख्यिकीय रूप से महत्वपूर्ण नहीं है।
• सूर्य के संपर्क में आने के लिए पी-वैल्यू 3.9E-8 (0.000000039) है। यह 0.05 महत्व के स्तर पर सांख्यिकीय रूप से महत्वपूर्ण है।
• पानी देने की आवृत्ति और सूर्य के संपर्क के बीच परस्पर क्रिया के लिए पी-मान 0.310898 है। यह 0.05 महत्व स्तर पर सांख्यिकीय रूप से महत्वपूर्ण नहीं है।

इन परिणामों से संकेत मिलता है कि सूरज की रोशनी पौधों की ऊंचाई पर सांख्यिकीय रूप से महत्वपूर्ण प्रभाव डालने वाला एकमात्र कारक है।

और चूंकि कोई अंतःक्रियात्मक प्रभाव नहीं है, सूर्य के संपर्क का प्रभाव पानी देने की आवृत्ति के प्रत्येक स्तर पर सुसंगत होता है।

सीधे शब्दों में कहें तो, चाहे किसी पौधे को रोजाना पानी दिया जाए या साप्ताहिक, इसका इस बात पर कोई प्रभाव नहीं पड़ता है कि सूरज का संपर्क पौधे को कैसे प्रभावित करता है।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल एनोवा मॉडल के बारे में अतिरिक्त जानकारी प्रदान करते हैं:

एनोवा में एफ मान और पी मान की व्याख्या कैसे करें
एनोवा में वर्गों के योग की गणना कैसे करें
एनोवा में उच्च F मान का क्या अर्थ है?