एसएएस में लॉजिस्टिक रिग्रेशन कैसे करें

लॉजिस्टिक रिग्रेशन एक ऐसी विधि है जिसका उपयोग हम रिग्रेशन मॉडल को फिट करने के लिए कर सकते हैं जब प्रतिक्रिया चर द्विआधारी होता है।

लॉजिस्टिक रिग्रेशन निम्नलिखित रूप का समीकरण खोजने के लिए अधिकतम संभावना अनुमान के रूप में ज्ञात विधि का उपयोग करता है:

लॉग[पी(एक्स) / (1 _– पी(एक्स))] = β ₀ + β ₁ एक्स ₁ + β ₂ एक्स ₂ + … + β _पी

सोना:

• एक्स _जे : जे ^वें पूर्वानुमानित चर
• β _j : j ^वें पूर्वानुमानित चर के लिए गुणांक का अनुमान

समीकरण के दाईं ओर का सूत्र लॉग ऑड्स की भविष्यवाणी करता है कि प्रतिक्रिया चर मान 1 लेता है।

निम्नलिखित चरण-दर-चरण उदाहरण दिखाता है कि एसएएस में लॉजिस्टिक रिग्रेशन मॉडल को कैसे फिट किया जाए।

चरण 1: डेटासेट बनाएं

सबसे पहले, हम 18 छात्रों के लिए निम्नलिखित तीन चरों पर जानकारी युक्त एक डेटासेट बनाएंगे:

• एक निश्चित कॉलेज में स्वीकृति (1 = हाँ, 0 = नहीं)
• जीपीए (1 से 4 का पैमाना)
• ACT स्कोर (1 से 36 का पैमाना)

 /*create dataset*/
data my_data;
    input acceptance gpa act;
    datalines ;
1 3 30
0 1 21
0 2 26
0 1 24
1 3 29
1 3 34
0 3 31
1 2 29
0 1 21
1 2 21
0 1 15
1 3 32
1 4 31
1 4 29
0 1 24
1 4 29
1 3 21
1 4 34
;
run ;

/*view dataset*/
proc print data =my_data;

चरण 2: लॉजिस्टिक रिग्रेशन मॉडल को फिट करें

इसके बाद, हम लॉजिस्टिक रिग्रेशन मॉडल को फिट करने के लिए प्रोक लॉजिस्टिक्स का उपयोग करेंगे, प्रतिक्रिया चर के रूप में “स्वीकृति” और भविष्यवक्ता चर के रूप में “जीपीए” और “एक्ट” का उपयोग करेंगे।

ध्यान दें : प्रतिक्रिया चर के 1 का मान लेने की संभावना की भविष्यवाणी करने के लिए एसएएस के लिए घटते हुए को निर्दिष्ट किया जाना चाहिए। डिफ़ॉल्ट रूप से, एसएएस इस संभावना की भविष्यवाणी करता है कि प्रतिक्रिया चर 0 का मान लेगा।

 /*fit logistic regression model*/
proc logistic data =my_data descending ;
  model acceptance = gpa act;
run ;

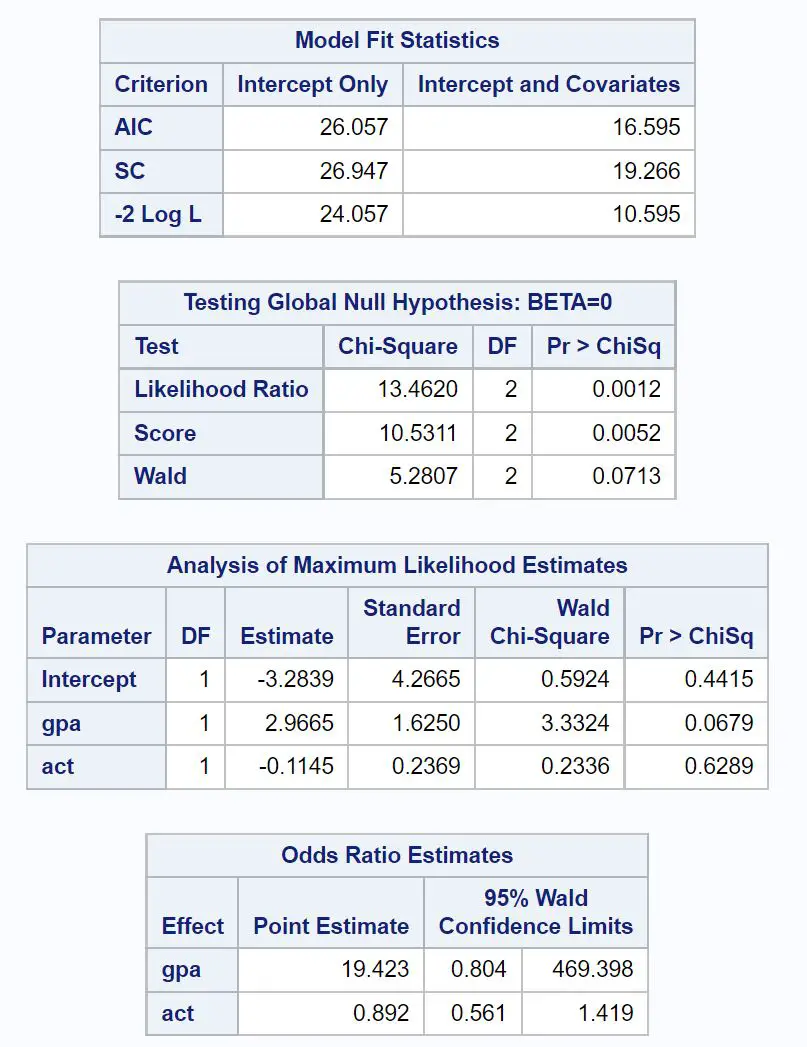
रुचि की पहली तालिका का शीर्षक मॉडल फ़िट सांख्यिकी है।

इस तालिका से हम मॉडल का AIC मान देख सकते हैं, जो 16.595 है। AIC मान जितना कम होगा, मॉडल उतना ही बेहतर डेटा फिट करने में सक्षम होगा।

हालाँकि, जिसे “अच्छा” एआईसी मान माना जाता है उसके लिए कोई सीमा नहीं है। बल्कि, हम एक ही डेटा सेट में कई मॉडलों के फिट की तुलना करने के लिए एआईसी का उपयोग करते हैं। सबसे कम AIC मान वाला मॉडल आमतौर पर सबसे अच्छा माना जाता है।

रुचि की अगली तालिका का शीर्षक वैश्विक शून्य परिकल्पना का परीक्षण: BETA=0 है ।

इस तालिका से, हम 0.0012 के संगत पी-मान के साथ 13.4620 का संभावना अनुपात ची-स्क्वायर मान देख सकते हैं।

चूँकि यह पी-वैल्यू 0.05 से कम है, यह हमें बताता है कि समग्र रूप से लॉजिस्टिक रिग्रेशन मॉडल सांख्यिकीय रूप से महत्वपूर्ण है।

इसके बाद, हम अधिकतम संभावना अनुमानों का विश्लेषण शीर्षक वाली तालिका में गुणांक अनुमानों का विश्लेषण कर सकते हैं।

इस तालिका से हम जीपीए और अधिनियम के लिए गुणांक देख सकते हैं, जो प्रत्येक चर में एक इकाई वृद्धि के लिए कॉलेज में स्वीकार किए जाने की लॉग बाधाओं में औसत परिवर्तन को दर्शाता है।

उदाहरण के लिए:

• GPA मान में एक इकाई की वृद्धि कॉलेज में स्वीकार किए जाने की लॉग बाधाओं में 2.9665 की औसत वृद्धि के साथ जुड़ी हुई है।
• ACT स्कोर में एक इकाई की वृद्धि कॉलेज में स्वीकार किए जाने की लॉग बाधाओं में औसत 0.1145 की कमी के साथ जुड़ी हुई है।

परिणाम में संबंधित पी-मान हमें यह भी अंदाजा देते हैं कि स्वीकार किए जाने की संभावना की भविष्यवाणी करने में प्रत्येक भविष्यवक्ता चर कितना प्रभावी है:

• जीपीए पी-वैल्यू: 0.0679
• अधिनियम पी-मूल्य: 0.6289

यह हमें बताता है कि GPA कॉलेज की स्वीकृति का सांख्यिकीय रूप से महत्वपूर्ण भविष्यवक्ता प्रतीत होता है, जबकि ACT स्कोर सांख्यिकीय रूप से महत्वपूर्ण प्रतीत नहीं होता है।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल बताते हैं कि एसएएस में अन्य प्रतिगमन मॉडल को कैसे फिट किया जाए:

एसएएस में सरल रैखिक प्रतिगमन कैसे करें
एसएएस में मल्टीपल लीनियर रिग्रेशन कैसे करें