पायथन में ओएलएस रिग्रेशन कैसे करें (उदाहरण के साथ)

साधारण न्यूनतम वर्ग (ओएलएस) प्रतिगमन एक ऐसी विधि है जो हमें एक ऐसी रेखा खोजने की अनुमति देती है जो एक या अधिक भविष्यवक्ता चर और एक प्रतिक्रिया चर के बीच संबंध का सबसे अच्छा वर्णन करती है।

यह विधि हमें निम्नलिखित समीकरण खोजने की अनुमति देती है:

ŷ = बी ₀ + बी ₁ एक्स

सोना:

• ŷ : अनुमानित प्रतिक्रिया मूल्य
• बी ₀ : प्रतिगमन रेखा की उत्पत्ति
• बी ₁ : प्रतिगमन रेखा का ढलान

यह समीकरण हमें भविष्यवक्ता और प्रतिक्रिया चर के बीच संबंध को समझने में मदद कर सकता है, और इसका उपयोग भविष्यवक्ता चर के मूल्य को देखते हुए प्रतिक्रिया चर के मूल्य की भविष्यवाणी करने के लिए किया जा सकता है।

निम्नलिखित चरण-दर-चरण उदाहरण दिखाता है कि पायथन में ओएलएस रिग्रेशन कैसे करें।

चरण 1: डेटा बनाएं

इस उदाहरण के लिए, हम 15 छात्रों के लिए निम्नलिखित दो चर वाला एक डेटासेट बनाएंगे:

• अध्ययन किए गए घंटों की कुल संख्या
• परीक्षा परीणाम

हम भविष्यवक्ता चर के रूप में घंटों और प्रतिक्रिया चर के रूप में परीक्षा स्कोर का उपयोग करके एक ओएलएस प्रतिगमन निष्पादित करेंगे।

निम्नलिखित कोड दिखाता है कि पांडा में यह नकली डेटासेट कैसे बनाया जाए:

 import pandas as pd

#createDataFrame
df = pd. DataFrame ({' hours ': [1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14],
                   ' score ': [64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89]})

#view DataFrame
print (df)

    hours score
0 1 64
1 2 66
2 4 76
3 5 73
4 5 74
5 6 81
6 6 83
7 7 82
8 8 80
9 10 88
10 11 84
11 11 82
12 12 91
13 12 93
14 14 89

चरण 2: ओएलएस प्रतिगमन निष्पादित करें

इसके बाद, हम भविष्यवक्ता चर के रूप में घंटों का उपयोग करके और प्रतिक्रिया चर के रूप में स्कोर का उपयोग करके ओएलएस प्रतिगमन करने के लिए स्टैटमॉडल मॉड्यूल में फ़ंक्शन का उपयोग कर सकते हैं:

 import statsmodels.api as sm

#define predictor and response variables
y = df[' score ']
x = df[' hours ']

#add constant to predictor variables
x = sm. add_constant (x)

#fit linear regression model
model = sm. OLS (y,x). fit ()

#view model summary
print ( model.summary ())

                            OLS Regression Results                            
==================================================== ============================
Dept. Variable: R-squared score: 0.831
Model: OLS Adj. R-squared: 0.818
Method: Least Squares F-statistic: 63.91
Date: Fri, 26 Aug 2022 Prob (F-statistic): 2.25e-06
Time: 10:42:24 Log-Likelihood: -39,594
No. Observations: 15 AIC: 83.19
Df Residuals: 13 BIC: 84.60
Model: 1                                         
Covariance Type: non-robust                                         
==================================================== ============================
                 coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
const 65.3340 2.106 31.023 0.000 60.784 69.884
hours 1.9824 0.248 7.995 0.000 1.447 2.518
==================================================== ============================
Omnibus: 4,351 Durbin-Watson: 1,677
Prob(Omnibus): 0.114 Jarque-Bera (JB): 1.329
Skew: 0.092 Prob(JB): 0.515
Kurtosis: 1.554 Cond. No. 19.2
==================================================== ============================

कोएफ़ कॉलम से, हम प्रतिगमन गुणांक देख सकते हैं और निम्नलिखित फिट प्रतिगमन समीकरण लिख सकते हैं:

स्कोर = 65.334 + 1.9824*(घंटे)

इसका मतलब यह है कि अध्ययन किया गया प्रत्येक अतिरिक्त घंटा औसत परीक्षा स्कोर में 1.9824 अंकों की वृद्धि से जुड़ा है।

65,334 का मूल मान हमें शून्य घंटे तक अध्ययन करने वाले छात्र के लिए औसत अपेक्षित परीक्षा स्कोर बताता है।

हम इस समीकरण का उपयोग किसी छात्र द्वारा अध्ययन किए गए घंटों की संख्या के आधार पर अपेक्षित परीक्षा स्कोर खोजने के लिए भी कर सकते हैं।

उदाहरण के लिए, एक छात्र जो 10 घंटे पढ़ाई करता है उसे 85.158 का परीक्षा स्कोर प्राप्त करना चाहिए:

स्कोर = 65.334 + 1.9824*(10) = 85.158

यहां शेष मॉडल सारांश की व्याख्या करने का तरीका बताया गया है:

• पी(>|टी|): यह मॉडल गुणांक से जुड़ा पी मान है। चूँकि घंटों के लिए पी-वैल्यू (0.000) 0.05 से कम है, हम कह सकते हैं कि घंटों और स्कोर के बीच सांख्यिकीय रूप से महत्वपूर्ण संबंध है।
• आर-वर्ग: यह हमें बताता है कि परीक्षा के अंकों में भिन्नता का प्रतिशत अध्ययन किए गए घंटों की संख्या से समझाया जा सकता है। इस मामले में, स्कोर में 83.1% भिन्नता को अध्ययन किए गए घंटों द्वारा समझाया जा सकता है।
• एफ-सांख्यिकी और पी-मूल्य: एफ-सांख्यिकी ( 63.91 ) और संबंधित पी-मूल्य ( 2.25ई-06 ) हमें प्रतिगमन मॉडल का समग्र महत्व बताते हैं, अर्थात क्या मॉडल में भविष्यवक्ता चर भिन्नता को समझाने में उपयोगी हैं। प्रतिक्रिया चर में. चूँकि इस उदाहरण में पी-वैल्यू 0.05 से कम है, हमारा मॉडल सांख्यिकीय रूप से महत्वपूर्ण है और स्कोर भिन्नता को समझाने में घंटों को उपयोगी माना जाता है।

चरण 3: सर्वोत्तम-फिट लाइन की कल्पना करें

अंत में, हम वास्तविक डेटा बिंदुओं पर फिट की गई प्रतिगमन रेखा को देखने के लिए matplotlib डेटा विज़ुअलाइज़ेशन पैकेज का उपयोग कर सकते हैं:

 import matplotlib. pyplot as plt

#find line of best fit
a, b = np. polyfit (df[' hours '], df[' score '], 1 )

#add points to plot
plt. scatter (df[' hours '], df[' score '], color=' purple ')

#add line of best fit to plot
plt. plot (df[' hours '], a*df[' hours ']+b)

#add fitted regression equation to plot
plt. text ( 1 , 90 , 'y = ' + '{:.3f}'.format(b) + ' + {:.3f}'.format(a) + 'x', size= 12 )

#add axis labels
plt. xlabel (' Hours Studied ')
plt. ylabel (' Exam Score ')

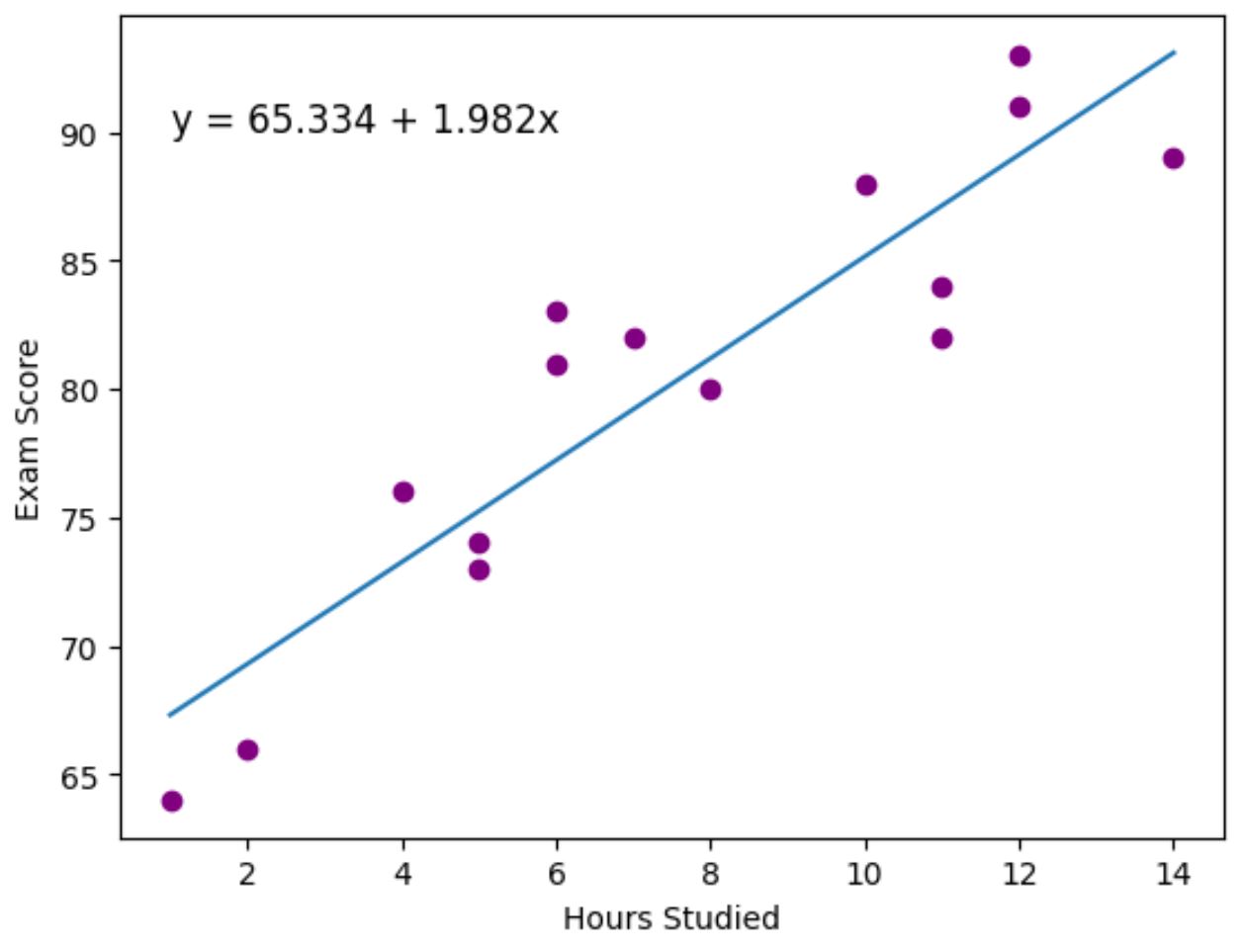
बैंगनी बिंदु वास्तविक डेटा बिंदुओं का प्रतिनिधित्व करते हैं और नीली रेखा फिटेड रिग्रेशन लाइन का प्रतिनिधित्व करती है।

हमने प्लॉट के ऊपरी बाएँ कोने में फिट किए गए प्रतिगमन समीकरण को जोड़ने के लिए plt.text() फ़ंक्शन का भी उपयोग किया।

ग्राफ़ को देखने से ऐसा प्रतीत होता है कि फिट की गई प्रतिगमन रेखा घंटे चर और स्कोर चर के बीच के संबंध को काफी अच्छी तरह से पकड़ लेती है।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल बताते हैं कि पायथन में अन्य सामान्य कार्य कैसे करें:

पायथन में लॉजिस्टिक रिग्रेशन कैसे करें
पायथन में एक्सपोनेंशियल रिग्रेशन कैसे करें
पायथन में प्रतिगमन मॉडल के एआईसी की गणना कैसे करें