केंडल का ताऊ: परिभाषा + उदाहरण
आंकड़ों में, सहसंबंध दो चर के बीच संबंध की ताकत और दिशा को संदर्भित करता है। सहसंबंध गुणांक का मान -1 से 1 तक हो सकता है, जिसमें -1 एक पूर्ण नकारात्मक संबंध को दर्शाता है, 0 कोई संबंध नहीं दर्शाता है, और 1 एक पूर्ण सकारात्मक संबंध को दर्शाता है।
सबसे अधिक इस्तेमाल किया जाने वाला सहसंबंध गुणांक पियर्सन सहसंबंध गुणांक है, जो दो संख्यात्मक चर के बीच रैखिक संबंध को मापता है।
एक कम आम तौर पर इस्तेमाल किया जाने वाला सहसंबंध गुणांक केंडल का ताऊ है, जो रैंक किए गए डेटा के दो स्तंभों के बीच संबंध को मापता है।
केंडल के ताऊ की गणना करने का सूत्र, जिसे अक्सर संक्षिप्त रूप में τ कहा जाता है, इस प्रकार है:
τ = (सीडी) / (सी+डी)
सोना:
C = मेल खाने वाली जोड़ियों की संख्या
डी = बेमेल जोड़ियों की संख्या
निम्नलिखित उदाहरण दिखाता है कि रैंक किए गए डेटा के दो स्तंभों के लिए केंडल के ताऊ रैंक सहसंबंध गुणांक की गणना करने के लिए इस सूत्र का उपयोग कैसे करें।
केंडल के ताऊ की गणना का उदाहरण
मान लें कि दो बास्केटबॉल कोच अपने खिलाड़ियों को सबसे खराब से सर्वश्रेष्ठ में 12 रैंक देते हैं। निम्नलिखित तालिका प्रत्येक कोच द्वारा खिलाड़ियों को दी गई रैंकिंग दिखाती है:
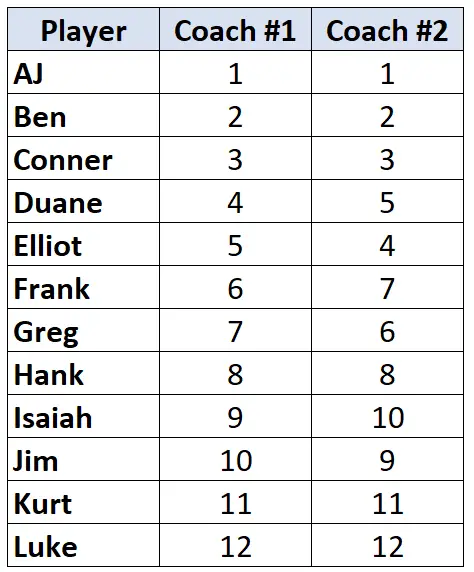
चूंकि हम रैंक किए गए डेटा के दो कॉलम के साथ काम कर रहे हैं, इसलिए दो कोचों की रैंकिंग के बीच संबंध की गणना करने के लिए केंडल के ताऊ का उपयोग करना उचित है। केंडल के ताऊ की गणना करने के लिए निम्नलिखित चरणों का पालन करें:
चरण 1: मेल खाने वाली जोड़ियों की संख्या गिनें।
केवल कोच #2 की रैंकिंग देखें। पहले खिलाड़ी से शुरू करते हुए, गिनें कि उसके नीचे कितने रैंक लम्बे हैं। उदाहरण के लिए, “1” के नीचे 11 संख्याएँ हैं जो बड़ी हैं, इसलिए हम 11 लिखेंगे:
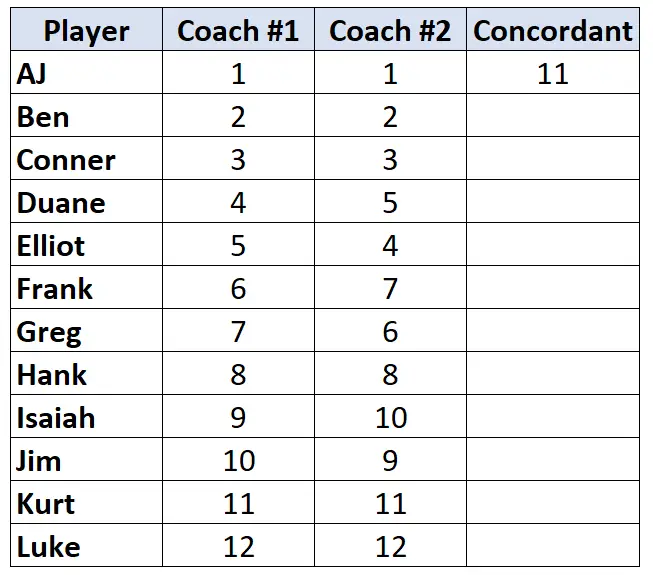
अगले खिलाड़ी के पास जाएँ और प्रक्रिया दोहराएँ। “2” के नीचे 10 संख्याएँ हैं जो बड़ी हैं, इसलिए हम 10 लिखेंगे:
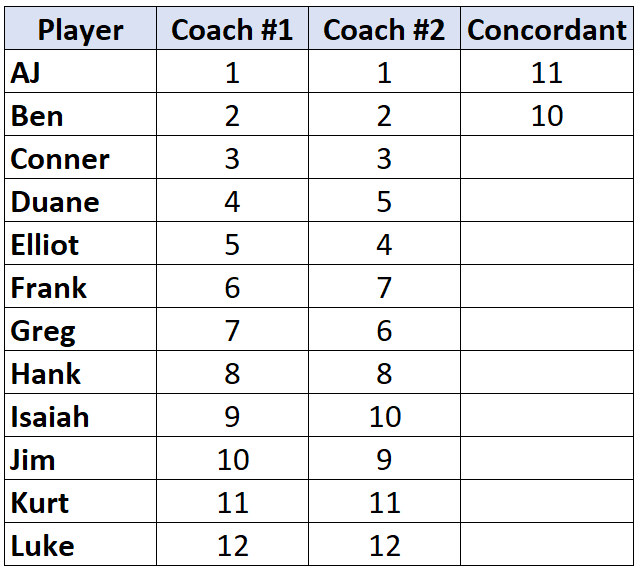
एक बार जब हम किसी ऐसे खिलाड़ी तक पहुँच जाते हैं जिसकी रैंक उससे पहले वाले खिलाड़ी से कम है, तो उसे बस वही मान दिया जाता है जो उससे पहले वाले खिलाड़ी को दिया जाता है। उदाहरण के लिए, इलियट की रैंक “4” है जो पिछले खिलाड़ी की रैंक “5” से कम है, इसलिए उसे बस उससे पहले वाले खिलाड़ी के समान ही मान दिया गया है:
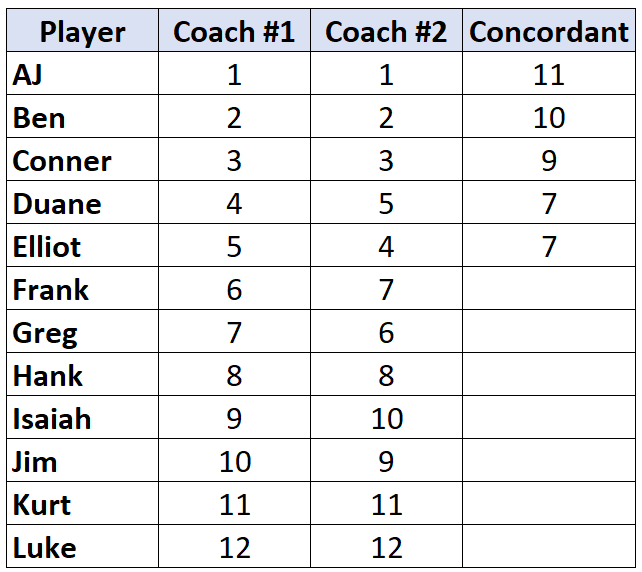
सभी खिलाड़ियों के लिए इस प्रक्रिया को दोहराएं:
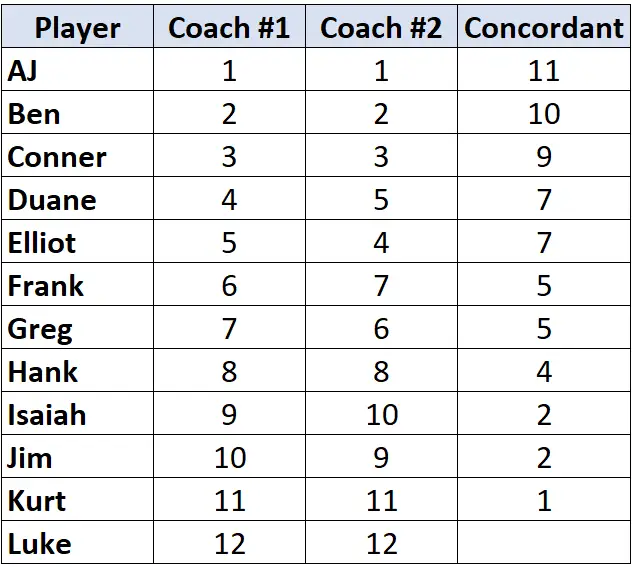
चरण 2: असंगत जोड़ियों की संख्या गिनें।
फिर से, केवल कोच #2 की रैंकिंग को देखें। प्रत्येक खिलाड़ी के लिए, गिनें कि उसके नीचे कितने रैंक छोटे हैं। उदाहरण के लिए, कोच #2 ने एजे को “1” रैंक दी और उसके नीचे के किसी भी खिलाड़ी की रैंक कम नहीं है। इस प्रकार, हम इसे 0 का मान देते हैं:
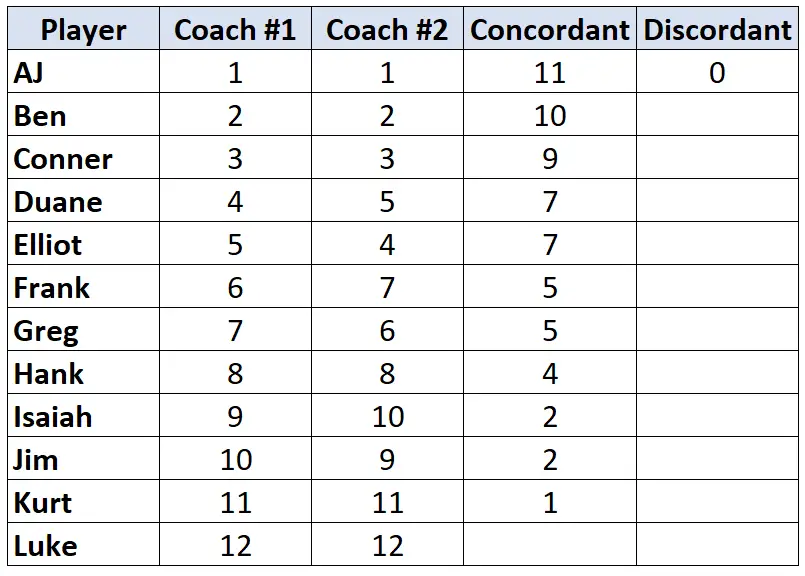
प्रत्येक खिलाड़ी के लिए इस प्रक्रिया को दोहराएं:
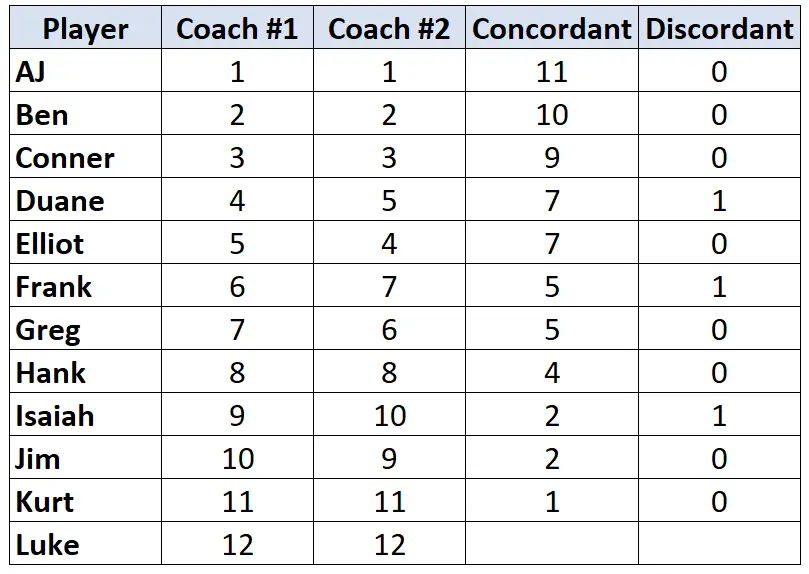
चरण 3: प्रत्येक कॉलम के योग की गणना करें और केंडल का ताऊ खोजें।
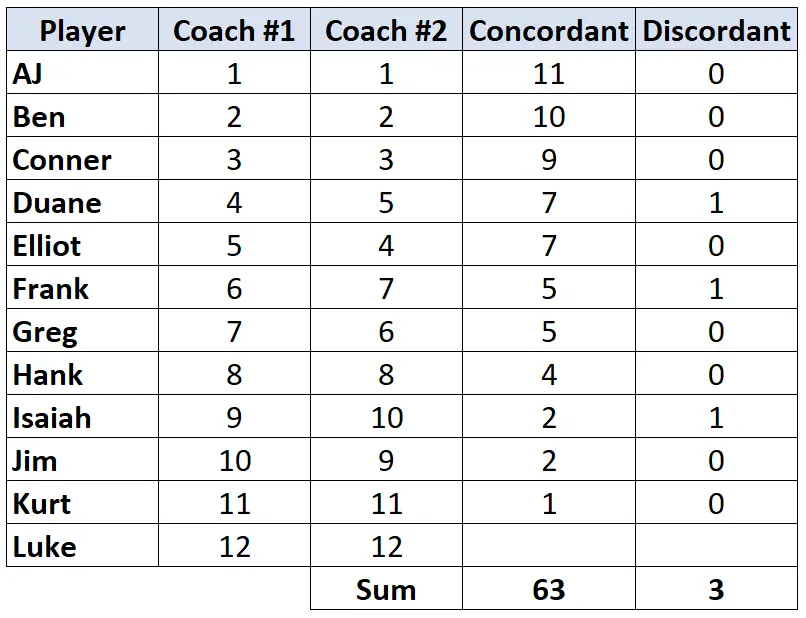
केंडल का ताऊ = (सीडी) / (सी+डी) = (63-3) / (63+3) = (60/66) = 0.909 ।
केंडल के ताऊ का सांख्यिकीय महत्व
जब आपके पास n=10 से अधिक जोड़े होते हैं, तो केंडल का ताऊ आम तौर पर एक सामान्य वितरण का अनुसरण करता है। आप केंडल के ताऊ के लिए z-स्कोर की गणना करने के लिए निम्नलिखित सूत्र का उपयोग कर सकते हैं:
z = 3τ*√ n(n-1) / √ 2(2n+5)
सोना:
τ = आपके द्वारा केंडल के ताऊ के लिए गणना किया गया मान
n = जोड़ियों की संख्या
पिछले उदाहरण के लिए z की गणना कैसे करें यहां बताया गया है:
z = 3(.909)*√ 12(12-1) / √ 2(2*12+5) = 4.11 ।
पी-वैल्यू जेड-स्कोर कैलकुलेटर का उपयोग करते हुए, हम देखते हैं कि इस जेड-स्कोर के लिए पी-वैल्यू 0.00004 है, जो 0.05 अल्फा स्तर पर सांख्यिकीय रूप से महत्वपूर्ण है। इस प्रकार, दोनों कोचों द्वारा खिलाड़ियों को दी गई रैंक के बीच सांख्यिकीय रूप से महत्वपूर्ण सहसंबंध है।
बोनस: आर में केंडल के ताऊ की गणना कैसे करें
आर सांख्यिकी सॉफ़्टवेयर में, आप दो वैक्टरों के लिए केंडल के ताऊ की गणना करने के लिए वीजीएएम लाइब्रेरी से kendall.tau() फ़ंक्शन का उपयोग कर सकते हैं, जो निम्नलिखित सिंटैक्स का उपयोग करता है:
केंडल.ताउ(x, y)
जहाँ x और y समान लंबाई के दो डिजिटल वेक्टर हैं।
निम्नलिखित कोड दर्शाता है कि पिछले उदाहरण में उपयोग किए गए सटीक डेटा के लिए केंडल के ताऊ की गणना कैसे करें:
#load VGAM library(VGAM) #create vector for each coach's rankings coach_1 <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12) coach_2 <- c(1, 2, 3, 5, 4, 7, 6, 8, 10, 9, 11, 12) #calculate Kendall's Tau kendall.tau(coach_1, coach_2) #[1] 0.9090909
ध्यान दें कि केंडल का ताऊ मान हमारे द्वारा मैन्युअल रूप से गणना किए गए मान से कैसे मेल खाता है।