घनत्व वक्र क्या हैं? (स्पष्टीकरण एवं उदाहरण)

घनत्व वक्र एक ग्राफ़ पर एक वक्र है जो डेटा के एक सेट में मूल्यों के वितरण का प्रतिनिधित्व करता है। यह तीन कारणों से उपयोगी है:

1. एक घनत्व वक्र हमें वितरण के “आकार” का एक अच्छा विचार देता है, जिसमें यह भी शामिल है कि वितरण में आवृत्ति मूल्यों के एक या अधिक “शिखर” हैं या नहीं और वितरण बाईं ओर तिरछा है या नहीं या सुधारना। सही। .

2. एक घनत्व वक्र हमें यह देखने की अनुमति देता है कि वितरण का माध्य और माध्यिका कहाँ से संबंधित है।

3. एक घनत्व वक्र हमें यह देखने की अनुमति देता है कि डेटा सेट में कितने प्रतिशत अवलोकन विभिन्न मूल्यों के बीच आते हैं।

सबसे प्रसिद्ध घनत्व वक्र घंटी के आकार का वक्र है जो सामान्य वितरण का प्रतिनिधित्व करता है।

घनत्व वक्रों को बेहतर ढंग से समझने के लिए, निम्नलिखित उदाहरण पर विचार करें।

उदाहरण: घनत्व वक्र बनाना और उसकी व्याख्या करना

मान लीजिए कि हमारे पास निम्नलिखित डेटासेट हैं जो एक निश्चित क्षेत्र में 20 विभिन्न पौधों की ऊंचाई (इंच में) दिखाते हैं:

4, 5, 5, 6, 6, 6, 6, 7, 7, 7, 7, 7, 8, 8, 8, 9, 9, 9, 2, 2

यदि हमने प्रत्येक मान की सापेक्ष आवृत्तियों को प्रदर्शित करने के लिए एक सरल हिस्टोग्राम बनाया, तो यह इस तरह दिखेगा:

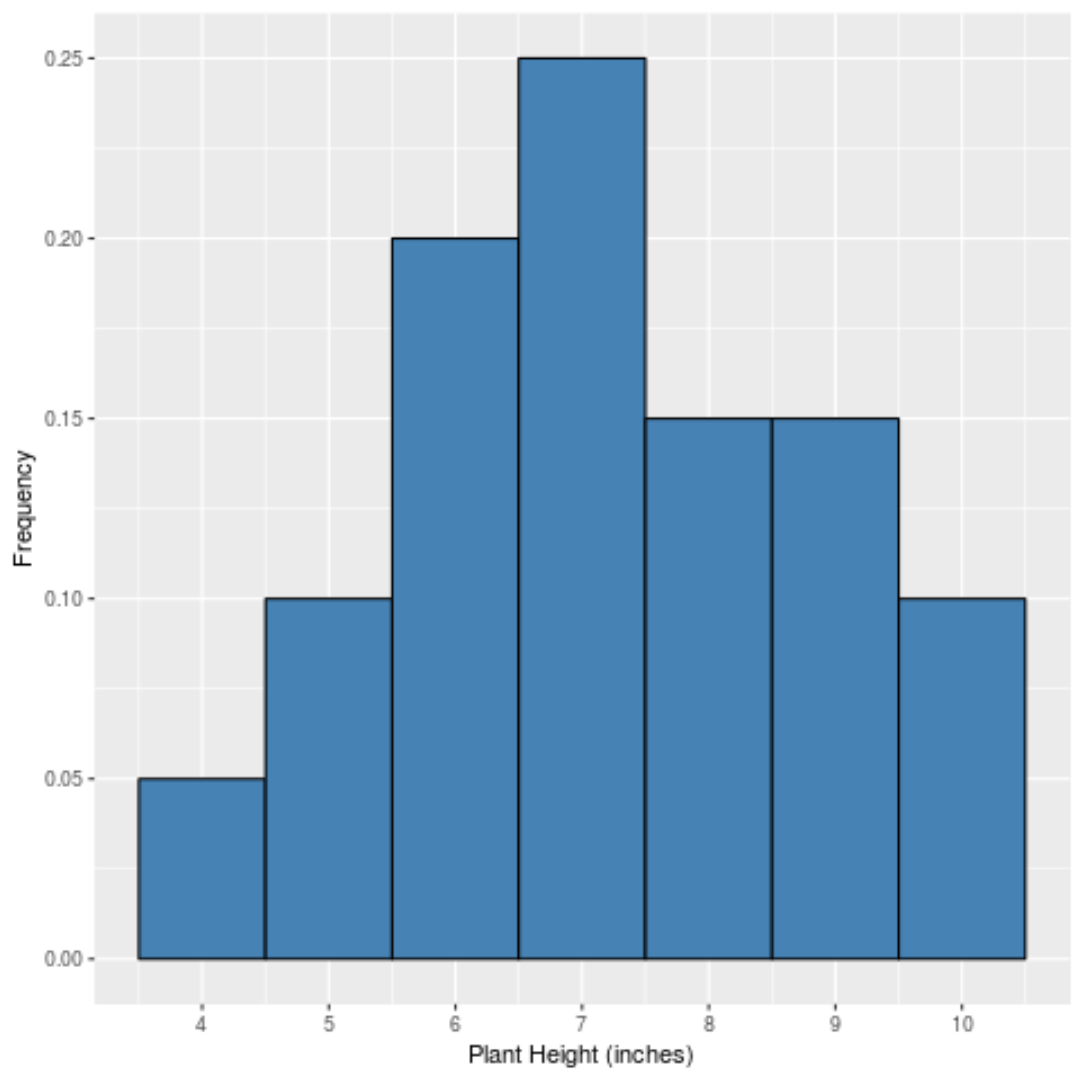
x-अक्ष डेटा मान दिखाता है और y-अक्ष सापेक्ष आवृत्ति दिखाता है (उदाहरण के लिए, मान “7” डेटासेट में 20 कुल मानों में से 5 बार दिखाई देता है, इसलिए इसकी सापेक्ष आवृत्ति 25% है या 0.25 .

और यदि हमने इस वितरण के “आकार” को पकड़ने के लिए एक घनत्व वक्र बनाया, तो यह इस तरह दिखेगा:

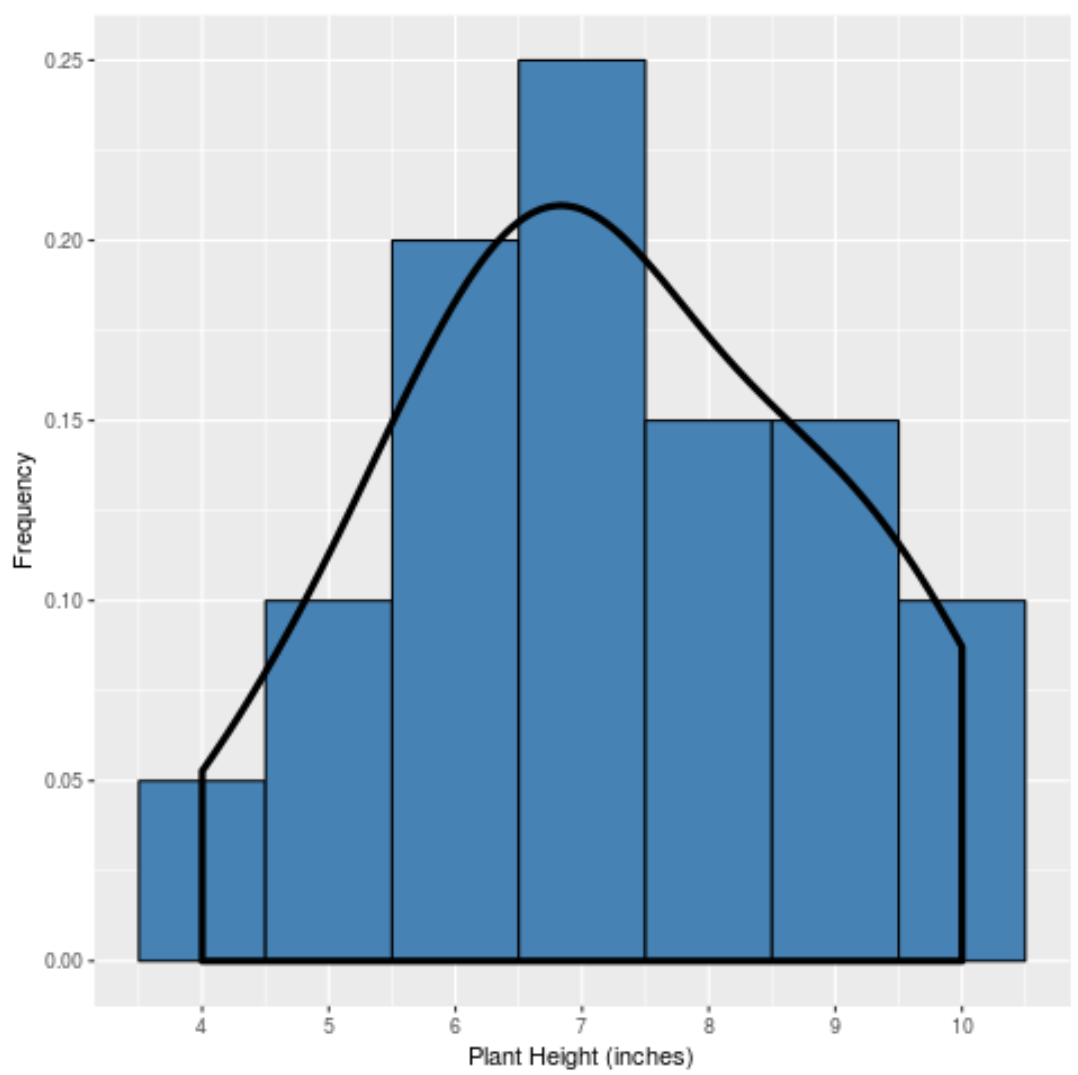
वक्र वितरण के केंद्र के पास सबसे ऊंचा होता है क्योंकि वहीं पर अधिकांश मान पाए जाते हैं। यह वितरण के अंत के पास भी सबसे कम है क्योंकि कम पौधे ये मान लेते हैं (जैसे ऊंचाई 4 इंच या 10 इंच)।

घनत्व वक्रों की व्याख्या कैसे करें

घनत्व वक्र सभी आकृतियों और आकारों में आते हैं और वे हमें किसी दिए गए डेटा सेट में मूल्यों के वितरण की त्वरित दृश्य समझ प्राप्त करने की अनुमति देते हैं। वे हमें कल्पना करने में मदद करने के लिए विशेष रूप से उपयोगी हैं:

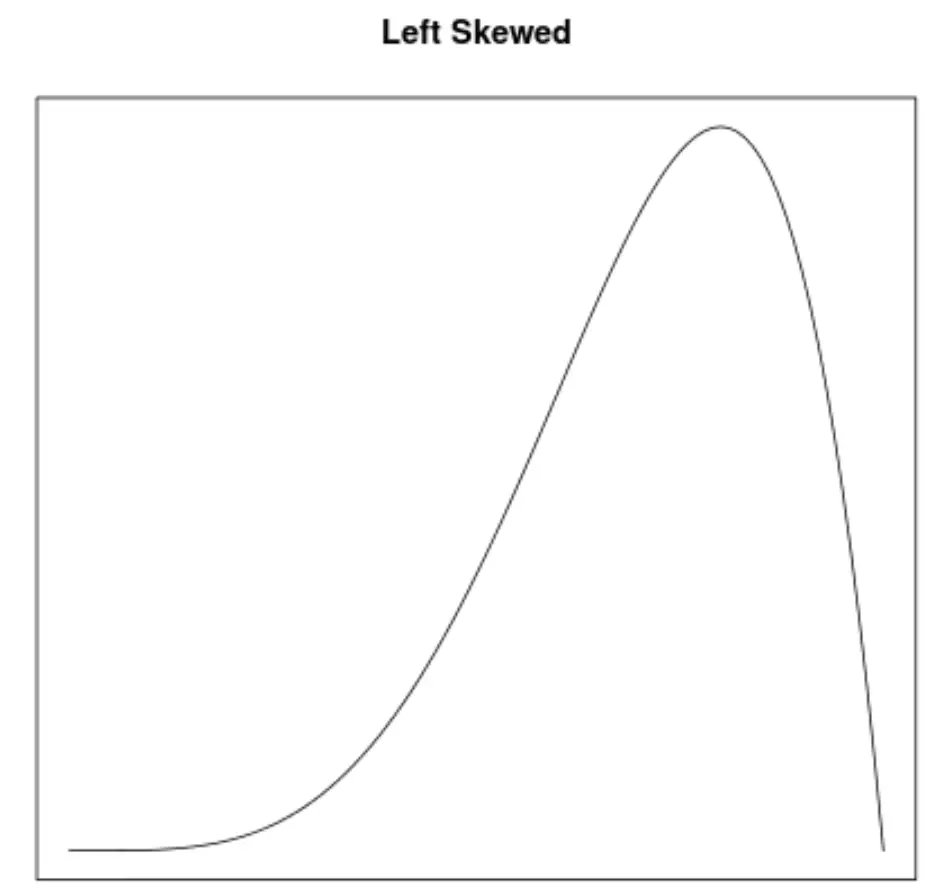
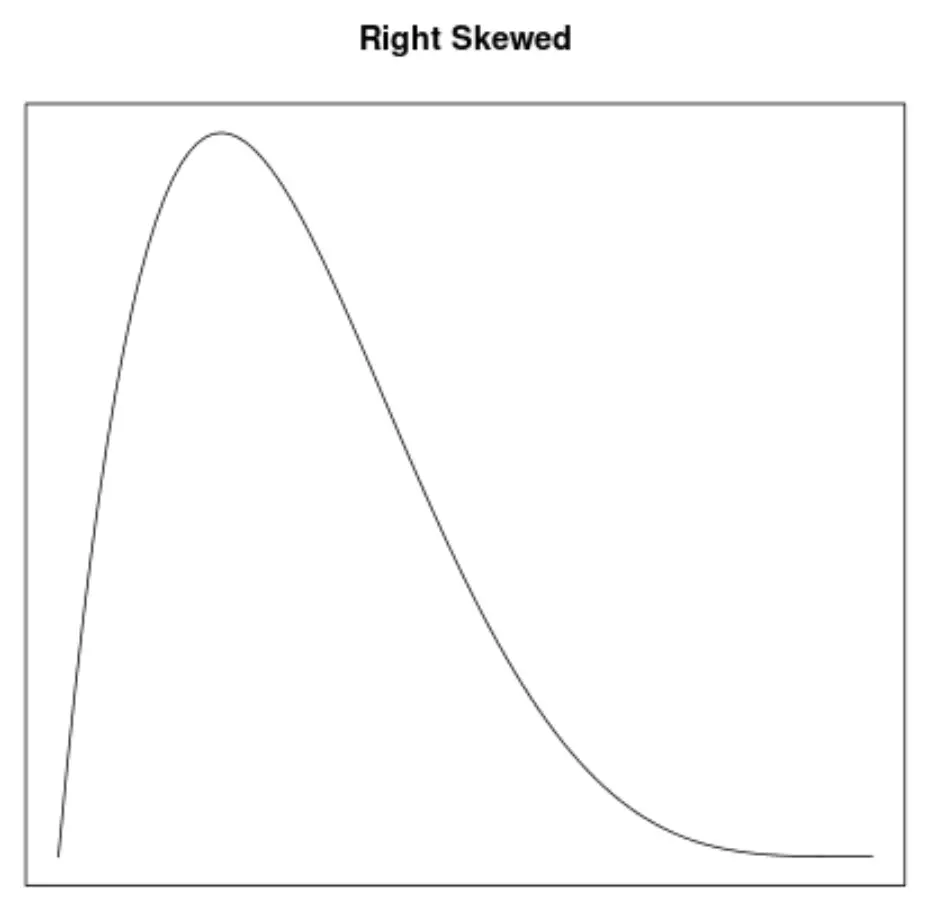
1. विषमता

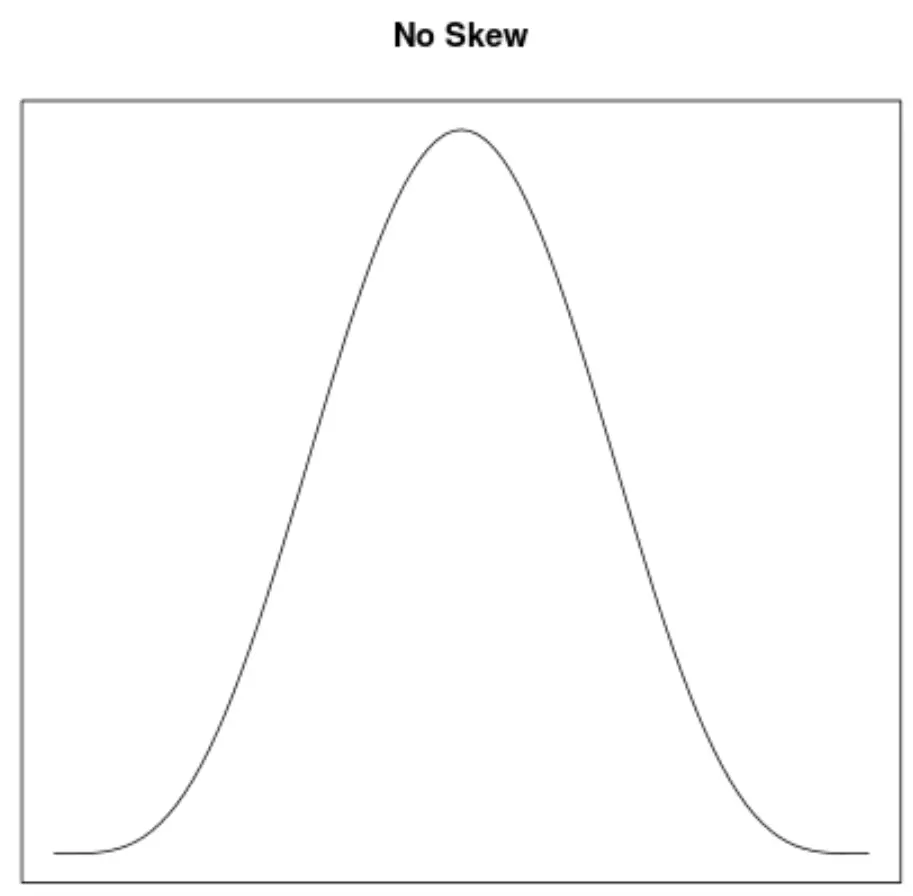
तिरछापन किसी वितरण की समरूपता का वर्णन करने का एक तरीका है। घनत्व वक्र हमें तुरंत यह देखने की अनुमति देते हैं कि ग्राफ बाएँ, दाएँ झुका हुआ है या कोई झुकाव नहीं है:

2. माध्य और माध्यिका का स्थान

घनत्व वक्र की विषमता के आधार पर, हम तुरंत बता सकते हैं कि दिए गए वितरण में माध्य या माध्य बड़ा है या नहीं। विशेष रूप से:

• यदि घनत्व वक्र असममित रहता है , तो माध्य माध्यिका से कम होता है।
• यदि घनत्व वक्र दाईं ओर तिरछा है, तो माध्य माध्यिका से अधिक है।
• यदि घनत्व वक्र में कोई विषमता नहीं है, तो माध्य माध्यिका के बराबर होता है।

3. चोटियों की संख्या

घनत्व वक्र हमें यह भी तुरंत देखने की अनुमति देते हैं कि किसी दिए गए वितरण में कितने “चोटियाँ” हैं। उपरोक्त प्रत्येक उदाहरण में, वितरणों का केवल एक शिखर था, इसलिए हम इन वितरणों को एकरूपक के रूप में वर्णित करेंगे।

हालाँकि, कुछ वितरणों में दो शिखर हो सकते हैं जिन्हें हम द्विमोडल वितरण कहते हैं। और दुर्लभ मामलों में हमारे पास दो या दो से अधिक चोटियों के साथ मल्टीमॉडल वितरण भी हो सकते हैं।

किसी दिए गए डेटा सेट के लिए बस एक घनत्व वक्र बनाकर, हम तुरंत देख सकते हैं कि वितरण में कितने शिखर हैं।

घनत्व वक्रों के गुण

घनत्व वक्रों में निम्नलिखित गुण होते हैं:

• वक्र के नीचे का क्षेत्रफल सदैव 100% तक जुड़ता है।
• वक्र कभी भी x-अक्ष से नीचे नहीं जायेगा।

विभिन्न वितरणों के लिए घनत्व वक्र बनाते या व्याख्या करते समय इन दो तथ्यों को ध्यान में रखें।

अतिरिक्त संसाधन

सापेक्ष आवृत्ति हिस्टोग्राम का परिचय
एक्सेल में बेल कर्व कैसे बनाएं
पायथन में बेल कर्व कैसे बनाएं