Ti-84 कैलकुलेटर पर z स्कोर की गणना कैसे करें

एक z-स्कोर हमें बताता है कि दिया गया मान माध्य से कितने मानक विचलन है। किसी दिए गए मान के z-स्कोर की गणना निम्नानुसार की जाती है:

z-स्कोर = (x – μ) / σ

सोना:

• एक्स: व्यक्तिगत मूल्य
• μ: जनसंख्या औसत
• σ: जनसंख्या मानक विचलन

यह ट्यूटोरियल बताता है कि TI-84 कैलकुलेटर पर z-स्कोर की गणना कैसे करें।

एकल मान के Z स्कोर की गणना कैसे करें

मान लीजिए कि एक वितरण सामान्यतः 12 के माध्य और 1.4 के मानक विचलन के साथ वितरित किया जाता है और हम एक व्यक्तिगत मान x = 14 के z-स्कोर की गणना करना चाहते हैं। TI-84 कैलकुलेटर में z-स्कोर की गणना करने के लिए, हम बस निम्न सूत्र टाइप करें:

यह हमें बताता है कि 14 के व्यक्तिगत मान का z-स्कोर 1.4286 है। दूसरे शब्दों में, मान 14 माध्य से 1.4286 मानक विचलन है।

एकाधिक मानों के Z स्कोर की गणना कैसे करें

इसके बजाय, मान लें कि हमारे पास डेटा मानों की एक सूची है और हम सूची में प्रत्येक मान के लिए z-स्कोर की गणना करना चाहते हैं। इस मामले में हम निम्नलिखित कदम उठा सकते हैं:

चरण 1: डेटा दर्ज करें।

सबसे पहले, हम डेटा मान दर्ज करेंगे। स्टेट दबाएँ फिर EDIT दबाएँ। कॉलम L1 में निम्नलिखित मान दर्ज करें:

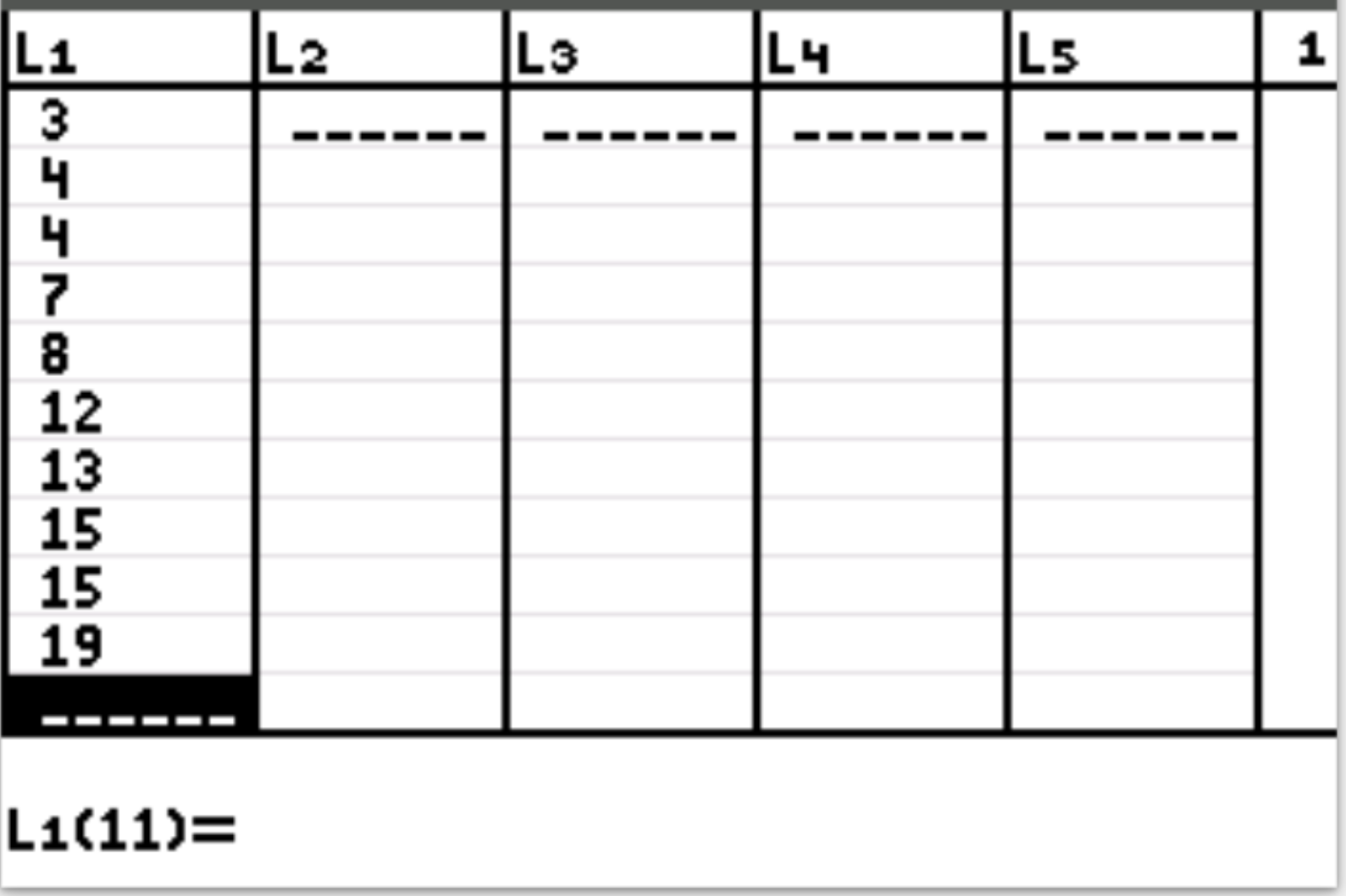
चरण 2: डेटा मानों का माध्य और मानक विचलन ज्ञात करें।

इसके बाद, हम डेटासेट का माध्य और मानक विचलन ज्ञात करेंगे। स्टेट दबाएँ और फिर CALC तक स्क्रॉल करें। आँकड़े 1-वार को हाइलाइट करें और एंटर दबाएँ।

सूची के लिए, सुनिश्चित करें कि L1 चुना गया है क्योंकि यह वह कॉलम है जिसमें हमने अपना डेटा दर्ज किया है। फ़्रीकलिस्ट को ख़ाली छोड़ें। कैलकुलेट को हाइलाइट करें और एंटर दबाएँ।

निम्नलिखित आउटपुट दिखाई देगा:

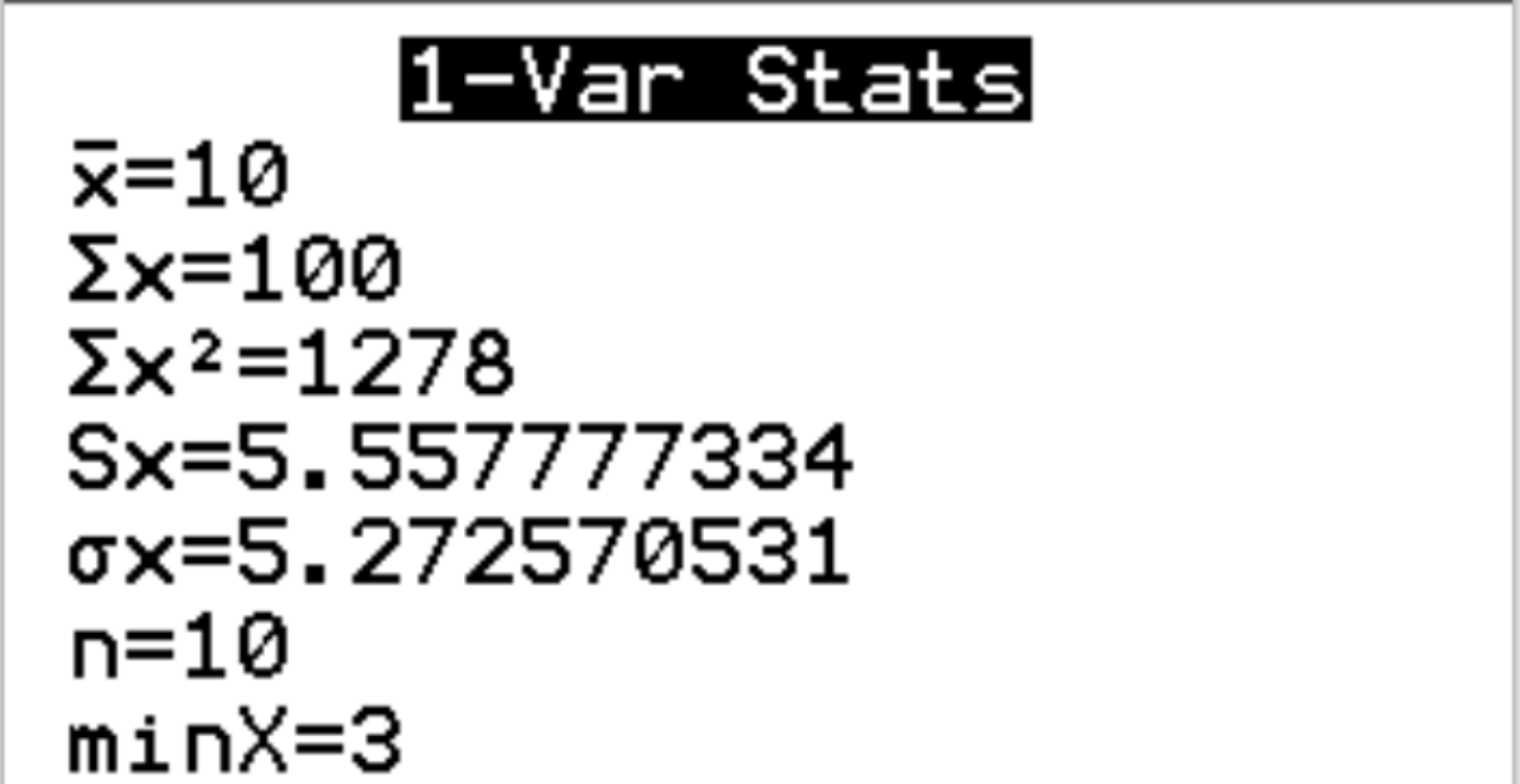
हम देख सकते हैं कि डेटासेट का माध्य x = 10 है और मानक विचलन s _x = 5.558 है। हम z-स्कोर की गणना के लिए अगले चरण में इन दो मानों का उपयोग करेंगे।

चरण 3: प्रत्येक z-स्कोर की गणना करने के लिए एक सूत्र का उपयोग करें।

इसके बाद, हम डेटासेट में प्रत्येक व्यक्तिगत मान के लिए z-स्कोर की गणना करेंगे। स्टेट दबाएँ फिर EDIT दबाएँ। L2 को हाइलाइट करें और सूत्र टाइप करें ( L1-10)/5.558 , फिर Enter दबाएँ। प्रत्येक व्यक्तिगत मान का z-स्कोर स्वचालित रूप से कॉलम L2 में दिखाई देगा:

नोट: सूत्र में “L1” दर्ज करने के लिए, 2 दबाएँ, फिर 1 दबाएँ।

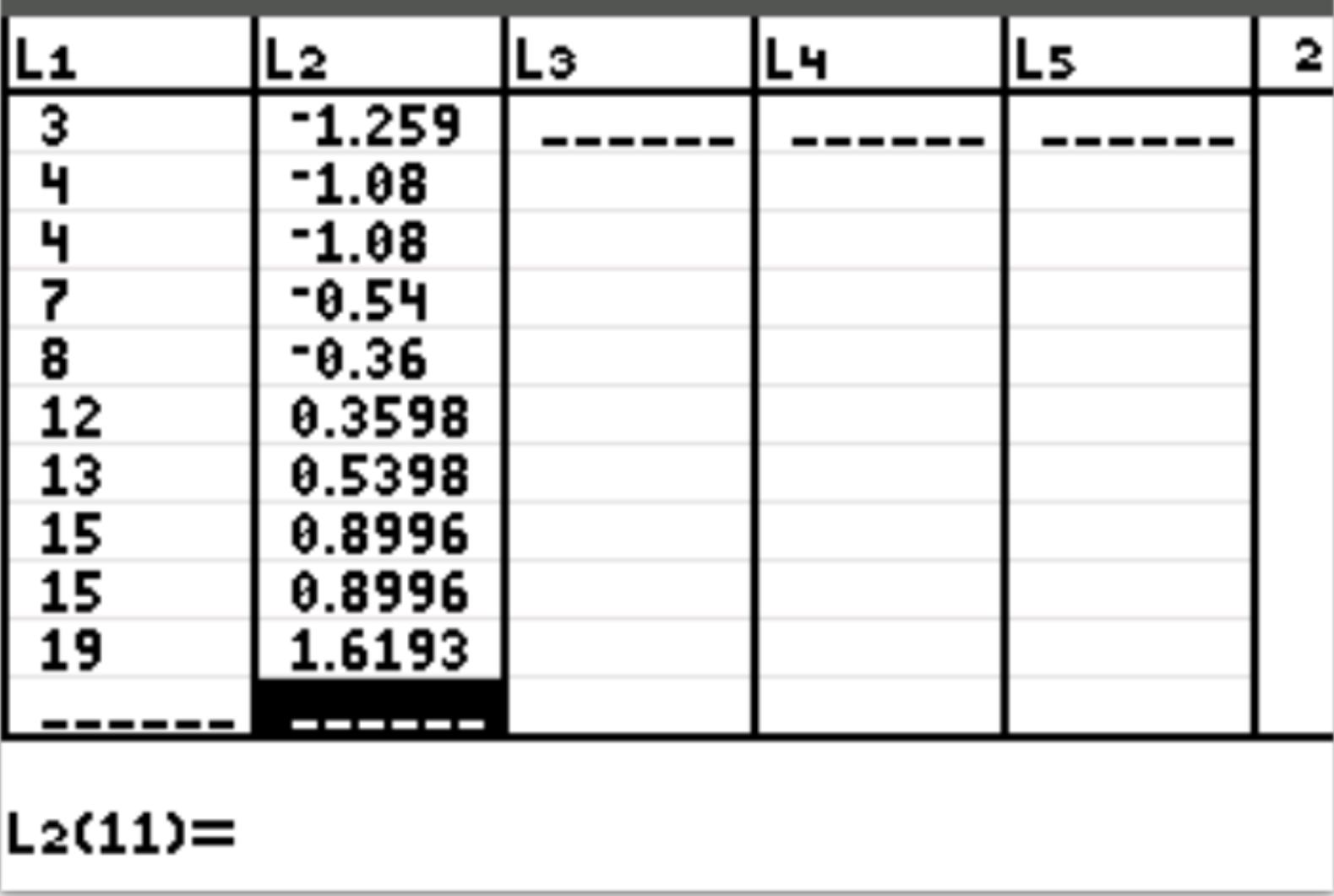
Z स्कोर की व्याख्या कैसे करें

याद रखें कि z-स्कोर हमें बस यह बताता है कि एक मान माध्य से कितने मानक विचलन है। A z स्कोर सकारात्मक, नकारात्मक या शून्य के बराबर हो सकता है:

• एक सकारात्मक z स्कोर इंगित करता है कि एक विशेष मान औसत से ऊपर है।
• एक नकारात्मक z स्कोर इंगित करता है कि एक विशेष मान औसत से नीचे है।
• शून्य का z-स्कोर इंगित करता है कि एक विशेष मान माध्य के बराबर है।

हमारे उदाहरण में, हमने पाया कि माध्य 10 था और मानक विचलन 5.558 था।

तो हमारे डेटासेट में पहला मान 3 था, जिसका z-स्कोर (3-10)/5.558 = -1.259 था। इसका मतलब है कि मान “3” माध्य से 1.259 मानक विचलन कम है।

हमारे डेटा सेट में अगला मान, 4, का z-स्कोर (4-10) / 5.558 = -1.08 था। इसका मतलब है कि मान “4” माध्य से 1.08 मानक विचलन कम है।

कोई मान माध्य से जितना दूर होगा, उस मान के लिए z-स्कोर का निरपेक्ष मान उतना ही अधिक होगा।

उदाहरण के लिए, मान 3, मान 4 की तुलना में माध्य से अधिक दूर है, जो बताता है कि 3 में बड़े निरपेक्ष मान के साथ z-स्कोर क्यों था।