एनोवा मान्यताओं की जांच कैसे करें

वन-वे एनोवा एक सांख्यिकीय परीक्षण है जिसका उपयोग यह निर्धारित करने के लिए किया जाता है कि तीन या अधिक स्वतंत्र समूहों के साधनों के बीच महत्वपूर्ण अंतर है या नहीं।

यहां एक उदाहरण दिया गया है जब हम एक-तरफ़ा एनोवा का उपयोग कर सकते हैं:

आप 90 छात्रों की एक कक्षा को यादृच्छिक रूप से 30 के तीन समूहों में विभाजित करते हैं। प्रत्येक समूह एक परीक्षा की तैयारी के लिए एक महीने के लिए एक अलग अध्ययन तकनीक का उपयोग करता है। महीने के अंत में, सभी छात्र समान परीक्षा देते हैं।

आप जानना चाहते हैं कि अध्ययन तकनीक का परीक्षा अंकों पर प्रभाव पड़ता है या नहीं। तो आप यह निर्धारित करने के लिए एक-तरफ़ा एनोवा निष्पादित करें कि क्या तीन समूहों के औसत स्कोर के बीच सांख्यिकीय रूप से महत्वपूर्ण अंतर है।

इससे पहले कि हम एक-तरफ़ा एनोवा निष्पादित कर सकें, हमें पहले यह सत्यापित करना होगा कि तीन धारणाएँ पूरी हुई हैं।

1. सामान्यता – प्रत्येक नमूना सामान्य रूप से वितरित जनसंख्या से लिया गया था।

2. समान प्रसरण – जिन जनसंख्याओं से नमूने लिए गए हैं उनके प्रसरण समान हैं।

3. स्वतंत्रता – प्रत्येक समूह के भीतर अवलोकन एक दूसरे से स्वतंत्र हैं और समूहों के भीतर अवलोकन यादृच्छिक नमूने द्वारा प्राप्त किए गए थे।

यदि ये धारणाएँ पूरी नहीं होती हैं, तो हमारे एकतरफा एनोवा के परिणाम विश्वसनीय नहीं हो सकते हैं।

इस लेख में हम बताते हैं कि इन धारणाओं की जांच कैसे करें और यदि उनमें से किसी का उल्लंघन होता है तो क्या करें।

धारणा #1: सामान्यता

एनोवा मानता है कि प्रत्येक नमूना सामान्य रूप से वितरित आबादी से लिया गया था।

R में इस परिकल्पना की जाँच कैसे करें:

इस परिकल्पना को सत्यापित करने के लिए, हम दो दृष्टिकोणों का उपयोग कर सकते हैं:

• हिस्टोग्राम या QQ प्लॉट का उपयोग करके परिकल्पना को दृश्य रूप से सत्यापित करें।
• शापिरो-विल्क, कोलमोगोरोव-स्मिरोनोव, जार्के-बैरे या डी’ऑगोस्टिनो-पियर्सन जैसे औपचारिक सांख्यिकीय परीक्षणों का उपयोग करके परिकल्पना को सत्यापित करें।

उदाहरण के लिए, मान लीजिए कि हम वजन घटाने के प्रयोग में भाग लेने के लिए 90 लोगों को भर्ती करते हैं, जिसमें हम यादृच्छिक रूप से 30 लोगों को एक महीने के लिए प्रोग्राम ए, प्रोग्राम बी या प्रोग्राम सी का पालन करने के लिए नियुक्त करते हैं। यह देखने के लिए कि क्या कार्यक्रम का वजन घटाने पर प्रभाव पड़ता है, हम एक-तरफ़ा एनोवा प्रदर्शन करना चाहते हैं। निम्नलिखित कोड दर्शाता है कि हिस्टोग्राम, क्यूक्यू प्लॉट और शापिरो-विल्क परीक्षण का उपयोग करके सामान्यता धारणा की जांच कैसे करें।

1. एनोवा मॉडल फिट करें।

 #make this example reproducible
set.seed(0)

#create data frame
data <- data. frame (program = rep(c(" A ", " B ", " C "), each = 30 ),
                   weight_loss = c(runif(30, 0, 3),
                                   runif(30, 0, 5),
                                   runif(30, 1, 7)))

#fit the one-way ANOVA model
model <- aov(weight_loss ~ program, data = data)

2. प्रतिक्रिया मूल्यों का एक हिस्टोग्राम बनाएं।

 #create histogram
hist(data$weight_loss)

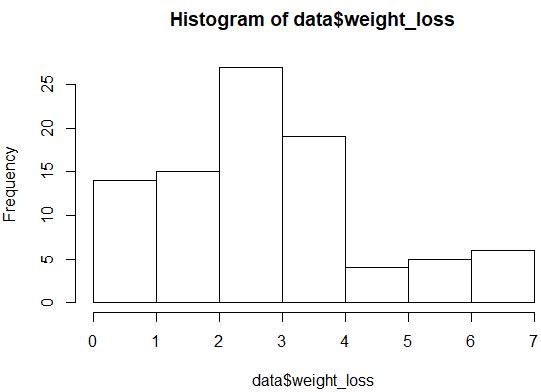
वितरण बहुत सामान्य रूप से वितरित नहीं दिखता है (उदाहरण के लिए यह “घंटी” आकार का नहीं है), लेकिन हम वितरण पर एक और नज़र डालने के लिए एक QQ प्लॉट भी बना सकते हैं।

3. अवशेषों का एक QQ प्लॉट बनाएं

 #create QQ plot to compare this dataset to a theoretical normal distribution
qqnorm(model$residuals)

#add straight diagonal line to plot
qqline(model$residuals) 

सामान्य तौर पर, यदि डेटा बिंदु QQ प्लॉट में एक सीधी विकर्ण रेखा के साथ स्थित होते हैं, तो डेटा सेट संभवतः सामान्य वितरण का अनुसरण करता है। इस मामले में, हम देख सकते हैं कि सिरों के साथ रेखा से ध्यान देने योग्य विचलन है, जो यह संकेत दे सकता है कि डेटा सामान्य रूप से वितरित नहीं है।

4. सामान्यता के लिए शापिरो-विल्क परीक्षण करें।

 #Conduct Shapiro-Wilk Test for normality
shapiro. test (data$weight_loss)

#Shapiro-Wilk normality test
#
#data: data$weight_loss
#W = 0.9587, p-value = 0.005999

शापिरो-विल्क परीक्षण शून्य परिकल्पना का परीक्षण करता है कि नमूने सामान्य वितरण से आते हैं जबकि वैकल्पिक परिकल्पना कि नमूने सामान्य वितरण से नहीं आते हैं। इस मामले में, परीक्षण का पी-मान 0.005999 है, जो 0.05 के अल्फा स्तर से कम है। इससे पता चलता है कि नमूने सामान्य वितरण का पालन नहीं करते हैं।

यदि इस धारणा का सम्मान न किया जाए तो क्या करें:

सामान्य तौर पर, एक तरफ़ा एनोवा को सामान्यता धारणा के उल्लंघन के खिलाफ काफी मजबूत माना जाता है जब तक कि नमूना आकार काफी बड़ा हो।

इसके अतिरिक्त, यदि आपके पास बहुत बड़े नमूने हैं, तो शापिरो-विल्क परीक्षण जैसे सांख्यिकीय परीक्षण लगभग हमेशा आपको बताएंगे कि आपका डेटा सामान्य नहीं है। इस कारण से, हिस्टोग्राम और क्यूक्यू प्लॉट जैसे चार्ट का उपयोग करके अपने डेटा का दृश्य निरीक्षण करना अक्सर सबसे अच्छा होता है। केवल ग्राफ़ को देखकर आप बहुत अच्छा अंदाज़ा लगा सकते हैं कि डेटा सामान्य रूप से वितरित है या नहीं।

यदि सामान्यता की धारणा का गंभीर रूप से उल्लंघन किया गया है या आप बस बहुत रूढ़िवादी होना चाहते हैं, तो आपके पास दो विकल्प हैं:

(1) अपने डेटा के प्रतिक्रिया मूल्यों को बदलें ताकि वितरण अधिक सामान्य रूप से वितरित हो।

(2) क्रुस्कल-वालिस परीक्षण जैसे समकक्ष गैर-पैरामीट्रिक परीक्षण करें जिसमें सामान्यता की धारणा की आवश्यकता नहीं होती है।

धारणा #2: समान विचरण

एनोवा मानता है कि जिन आबादी से नमूने लिए गए हैं उनकी भिन्नताएं बराबर हैं।

R में इस परिकल्पना की जाँच कैसे करें:

हम दो दृष्टिकोणों का उपयोग करके आर में इस परिकल्पना को सत्यापित कर सकते हैं:

• बॉक्सप्लॉट का उपयोग करके परिकल्पना को दृश्य रूप से सत्यापित करें।
• बार्टलेट परीक्षण जैसे औपचारिक सांख्यिकीय परीक्षणों का उपयोग करके परिकल्पना का परीक्षण करें।

निम्नलिखित कोड दर्शाता है कि यह कैसे करना है, उसी नकली वजन घटाने वाले डेटासेट का उपयोग करके जो हमने पहले बनाया था।

1. बॉक्स प्लॉट बनाएं.

 #Create box plots that show distribution of weight loss for each group
boxplot(weight_loss ~ program, xlab=' Program ', ylab=' Weight Loss ', data=data)

प्रत्येक समूह में वजन घटाने में भिन्नता को प्रत्येक बॉक्सप्लॉट की लंबाई से देखा जा सकता है। बॉक्स जितना लंबा होगा, विचरण उतना ही अधिक होगा। उदाहरण के लिए, हम देख सकते हैं कि प्रोग्राम ए और प्रोग्राम बी की तुलना में प्रोग्राम सी में प्रतिभागियों के लिए भिन्नता थोड़ी अधिक है।

2. बार्टलेट परीक्षण करें.

 #Create box plots that show distribution of weight loss for each group
bartlett. test (weight_loss ~ program, data=data)

#Bartlett test of homogeneity of variances
#
#data: weight_loss by program
#Bartlett's K-squared = 8.2713, df = 2, p-value = 0.01599

बार्टलेट परीक्षण शून्य परिकल्पना का परीक्षण करता है कि नमूनों में समान भिन्नताएं हैं जबकि वैकल्पिक परिकल्पना है कि नमूनों में समान भिन्नताएं नहीं हैं। इस मामले में, परीक्षण का पी-मान 0.01599 है, जो 0.05 के अल्फा स्तर से कम है। इससे पता चलता है कि सभी नमूनों में समान भिन्नता नहीं है।

यदि इस धारणा का सम्मान न किया जाए तो क्या करें:

सामान्य तौर पर, एक-तरफ़ा एनोवा को समान भिन्नताओं की धारणा के उल्लंघन के लिए काफी मजबूत माना जाता है, जब तक कि प्रत्येक समूह का नमूना आकार समान हो।

हालाँकि, यदि नमूना आकार समान नहीं हैं और इस धारणा का गंभीर रूप से उल्लंघन किया गया है, तो आप इसके बजाय क्रुस्कल-वालिस परीक्षण चला सकते हैं, जो एक-तरफ़ा एनोवा का गैर-पैरामीट्रिक संस्करण है।

धारणा #3: स्वतंत्रता

एनोवा मानती है:

• प्रत्येक समूह के अवलोकन अन्य सभी समूहों के अवलोकनों से स्वतंत्र होते हैं।
• प्रत्येक समूह के भीतर अवलोकन एक यादृच्छिक नमूने द्वारा प्राप्त किए गए थे।

इस परिकल्पना को कैसे सत्यापित करें:

ऐसा कोई औपचारिक परीक्षण नहीं है जिसका उपयोग आप यह सत्यापित करने के लिए कर सकें कि प्रत्येक समूह में अवलोकन स्वतंत्र हैं और वे यादृच्छिक नमूने द्वारा प्राप्त किए गए थे। इस धारणा को संतुष्ट करने का एकमात्र तरीका यादृच्छिक डिज़ाइन का उपयोग करना है।

यदि इस धारणा का सम्मान न किया जाए तो क्या करें:

दुर्भाग्य से, यदि यह धारणा पूरी नहीं हुई तो आप बहुत कुछ नहीं कर सकते। सीधे शब्दों में कहें, यदि डेटा इस तरह से एकत्र किया गया था कि प्रत्येक समूह में अवलोकन अन्य समूहों में अवलोकनों से स्वतंत्र नहीं थे, या यदि प्रत्येक समूह के भीतर अवलोकन यादृच्छिक प्रक्रिया द्वारा प्राप्त नहीं किए गए थे, तो एनोवा परिणाम विश्वसनीय नहीं होंगे .

यदि यह धारणा पूरी नहीं होती है, तो सबसे अच्छी बात यह है कि यादृच्छिक डिज़ाइन का उपयोग करके प्रयोग को फिर से बनाया जाए।

अग्रिम पठन:

आर में एकतरफ़ा एनोवा कैसे निष्पादित करें
एक्सेल में वन-वे एनोवा कैसे करें