तना और पत्ती आरेख
यह आलेख बताता है कि सांख्यिकी में तना और पत्ती आरेख क्या हैं और उनका उपयोग किस लिए किया जाता है। इसलिए आप जानेंगे कि स्टेम-लीफ आरेख का निर्माण कैसे किया जाता है, इस प्रकार के सांख्यिकीय ग्राफ़ के लिए हल किए गए अभ्यास और अंत में, स्टेम-लीफ आरेख के फायदे और नुकसान क्या हैं।
तना-पत्ती आरेख क्या है?
तना और पत्ती आरेख एक प्रकार का सांख्यिकीय आरेख है जिसमें मात्रात्मक डेटा का एक सेट दर्शाया जाता है।
स्टेम-लीफ आरेख में, प्रत्येक डेटा बिंदु को लीफ द्वारा अलग किया जाता है, जो इसका अंतिम अंक है, और स्टेम , जो शेष अंक हैं। तो, तना-पत्ती आरेख में, प्रत्येक पत्ती को उसके संबंधित तने की रेखा पर रखा जाता है।
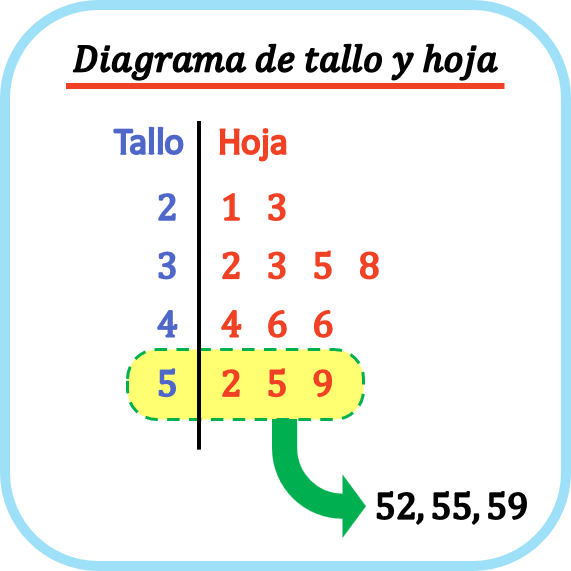
इस तरह, तने और पत्ती के प्लॉट सांख्यिकीय डेटा के एक सेट को ग्राफ़िक रूप से प्रस्तुत करने में मदद करते हैं और वितरण के आकार की कल्पना करने में भी मदद करते हैं।
तना और पत्ती आरेख को स्टेम और पत्ती आरेख के रूप में भी जाना जाता है, यह नाम अंग्रेजी से आया है।
तने और पत्ती का आलेखन हिस्टोग्राम के समान ही है, हालांकि इस अन्य प्रकार के सांख्यिकीय ग्राफ़ का उपयोग बड़े नमूना आकारों के लिए किया जाता है।
तने और पत्ती का आरेख कैसे बनाएं
तना और पत्ती आरेख बनाने के लिए, इन चरणों का पालन करें:
- डेटा को सबसे छोटे से सबसे बड़े तक क्रमबद्ध करें।
- यदि आवश्यक हो, तो संख्याओं को तब तक गोल करें जब तक उनमें अंकों की वांछित संख्या न हो जाए।
- तय करें कि तने और पत्ती के बीच किस आकृति में कट लगाया जाएगा, अर्थात पत्तियों पर कितनी आकृतियाँ होंगी, यह निर्धारित करें। आमतौर पर, शीट को प्रत्येक डेटा आइटम का केवल अंतिम अंक शामिल करने के लिए डिज़ाइन किया गया है।
- तने और पत्ती आरेख में डेटा के प्रत्येक टुकड़े का प्रतिनिधित्व करें। तने को बाएं स्तंभ में आरोही क्रम में रखा गया है, जबकि पत्तियों को दाएं स्तंभ में उनके संबंधित तने की ऊंचाई पर और आरोही क्रम में भी रखा गया है।
तना और पत्ती प्लॉट का उदाहरण
तो आप देख सकते हैं कि तने और पत्ती का आरेख कैसे बनाया जाता है, हम नीचे दो उदाहरण हल करते हैं: एक बिना दशमलव के और दूसरा दशमलव के साथ।
उदाहरण 1
- निम्नलिखित डेटा श्रृंखला को तने और पत्ती आरेख में प्लॉट करें:

इस मामले में डेटा पहले से ही ऑर्डर और राउंड किया गया है, इसलिए इन दो चरणों को निष्पादित करना आवश्यक नहीं है। इसलिए, चूँकि संख्याओं में दो अंक होते हैं, उन्हें इस तरह दर्शाया जाएगा कि काल ग्राफ़ का आधार और काल पत्तियाँ हों।
हम पहले आरेख के मूल का प्रतिनिधित्व करेंगे। डेटा का काल 9 तक चला जाता है, इसलिए हम प्रत्येक दस के लिए एक पंक्ति बनाते हैं:

और फिर हम पत्तों को निरूपित करते हैं, इसके लिए हम प्रत्येक डेटा की इकाई को उसकी संगत पंक्ति में रखते हैं। उदाहरण के लिए, संख्या 57 मूल 5 पर जाएगी और दाहिने कॉलम में हम 7 जोड़ देंगे।
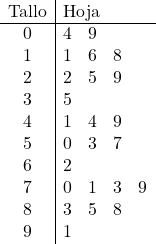
और इस तरह, सभी नमूना डेटा को तने और पत्ती के प्लॉट में दर्शाया गया था।
उदाहरण 2
- स्टेम-एंड-लीफ प्लॉट का उपयोग करके निम्नलिखित दो डेटा नमूनों की दशमलव से तुलना करें।


जैसा कि आप इस अभ्यास में देखेंगे, दो सांख्यिकीय नमूनों का प्रतिनिधित्व करने के लिए एक तने और पत्ती के प्लॉट का उपयोग किया जा सकता है। इसलिए, हम डेटा के दोनों सेटों को एक ही स्टेम-एंड-लीफ प्लॉट पर प्लॉट करेंगे: एक बाईं ओर और एक दाईं ओर। इस प्रकार के प्लॉट को डबल-स्टेम्ड स्टेम-एंड-लीफ प्लॉट कहा जाता है।
इस मामले में, हम संख्याओं के पूरे भाग को आरेख के आधार के रूप में लेंगे और दूसरी ओर, दशमलव आरेख के पत्ते होंगे। इसलिए हम सभी भागों को रखकर तने और पत्ती का लेआउट बनाते हैं:
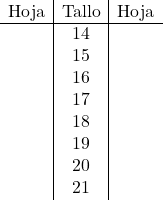
और अब हम प्रत्येक डेटा की शीट को उसके अनुरूप स्टेम में रखते हैं:
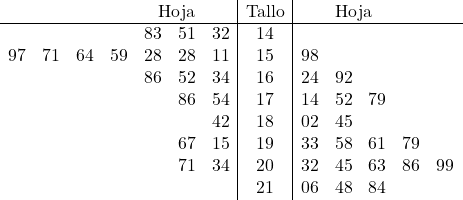
ग्राफ़िक रूप से डेटा का प्रतिनिधित्व करके, हम आसानी से इसकी तुलना कर सकते हैं। विशेष रूप से, हम देखते हैं कि दाईं ओर का नमूना डेटा बाईं ओर के नमूने से थोड़ा बड़ा है, इसलिए इसका औसत भी बड़ा होगा। इस प्रकार, सांख्यिकीय अध्ययन के उद्देश्य के आधार पर, हमें इस या उस नमूने को चुनने में रुचि होगी।
ध्यान रखें कि आपको न केवल यह जानना होगा कि स्लैश और ब्लेड चार्ट कैसे बनाया जाए, बल्कि आपको यह भी जानना होगा कि चार्ट की व्याख्या कैसे की जाए।
तना और पत्ती प्लॉट के फायदे और नुकसान
तने और पत्ती वाले भूखंड की विशेषताओं के कारण, इस प्रकार के भूखंडों के निम्नलिखित फायदे और नुकसान हैं:
फ़ायदा:
- तनों और पत्तियों का पता लगाने से आप वितरण का आकार देख सकते हैं।
- डबल-स्टेम स्टेम-एंड-लीफ प्लॉट का उपयोग करके दो वितरणों की तुलना की जा सकती है।
- यह आपको डेटा सेट में आउटलेर्स को तुरंत पहचानने की अनुमति देता है।
- आप आंखों से डेटा श्रृंखला का मोड निर्धारित कर सकते हैं।
नुकसान:
- तना और पत्ती आरेख का उपयोग कम से कम किया जा रहा है क्योंकि कंप्यूटर सॉफ़्टवेयर जल्दी से अधिक जटिल ग्राफ़ बना सकता है।
- प्रस्तुत करने के लिए नमूना आकार सीमित है, आम तौर पर 15 और 150 डेटा बिंदुओं के बीच।
- केवल मात्रात्मक डेटा प्रस्तुत किया जा सकता है।