त्रिकोणीय वितरण का परिचय
त्रिकोणीय वितरण त्रिकोण के आकार के संभाव्यता घनत्व फ़ंक्शन के साथ एक सतत संभाव्यता वितरण है।
इसे तीन मानों द्वारा परिभाषित किया गया है:
- न्यूनतम मूल्य है
- अधिकतम मान बी
- अधिकतम मान सी
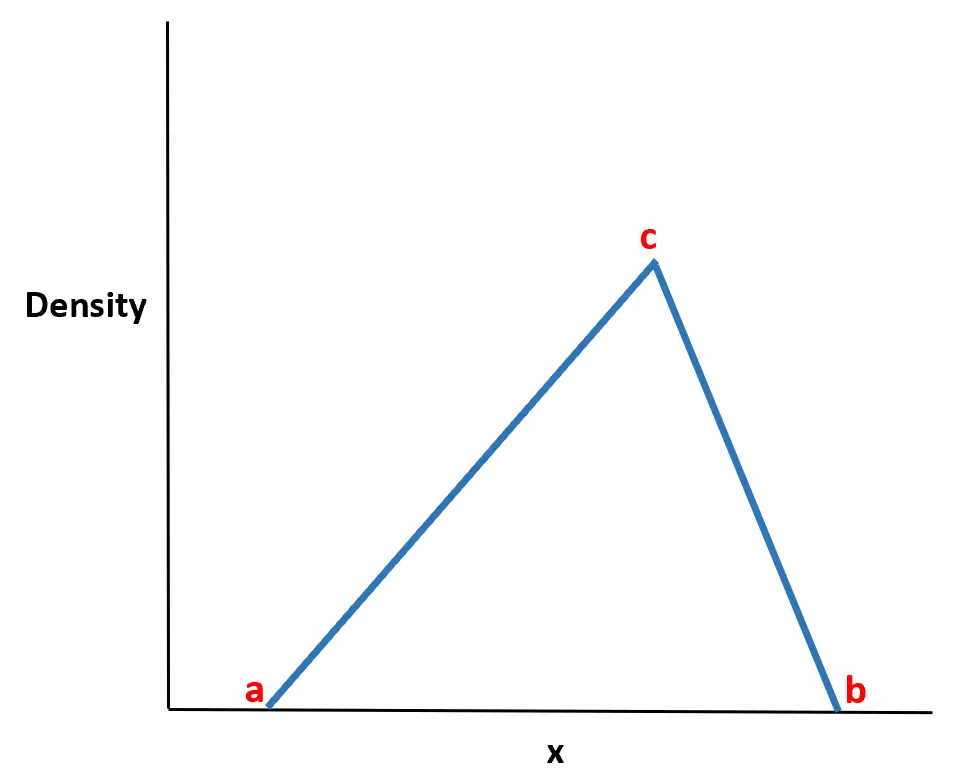
वितरण का नाम इस तथ्य से आता है कि संभाव्यता घनत्व फ़ंक्शन का आकार त्रिभुज जैसा होता है।
यह पता चला है कि यह वितरण वास्तविक दुनिया में बेहद उपयोगी है क्योंकि हम अक्सर न्यूनतम मूल्य (ए), अधिकतम मूल्य (बी), और सबसे संभावित मूल्य (सी) का अनुमान लगा सकते हैं जो एक यादृच्छिक चर लेगा। अक्सर केवल इन तीन मानों को जानकर त्रिकोणीय वितरण का उपयोग करके यादृच्छिक चर के व्यवहार को मॉडल किया जा सकता है।
उदाहरण के लिए, एक रेस्तरां अनुमान लगा सकता है कि आने वाले सप्ताह के लिए उसकी कुल बिक्री न्यूनतम $10,000, अधिकतम $30,000 और संभवतः $25,000 होगी।

केवल इन तीन संख्याओं का उपयोग करके, वे एक निश्चित संख्या में बिक्री करने की संभावना निर्धारित करने के लिए त्रिकोणीय वितरण का उपयोग कर सकते हैं।
त्रिकोणीय वितरण के गुण
त्रिकोणीय वितरण में निम्नलिखित गुण हैं:
पीडीएफ:
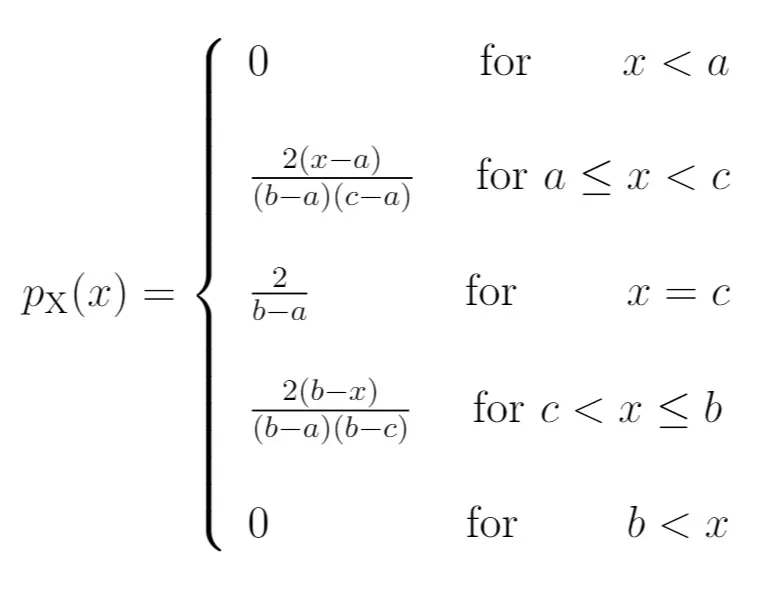
सीडीएफ:
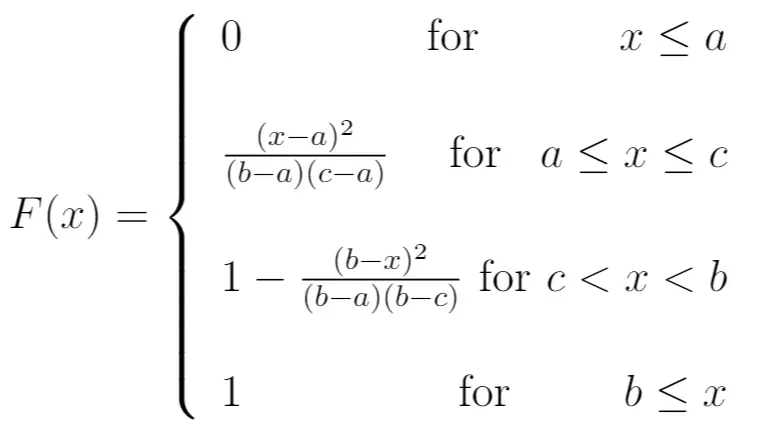
औसत: (ए + बी + सी) / 3
मोड: सी
प्रसरण: (ए 2 + बी 2 + सी 2 – एबी – एसी – बीसी) / 18
त्रिकोणीय वितरण का उपयोग करने का उदाहरण
आइए पिछले उदाहरण पर वापस जाएँ। मान लीजिए कि एक रेस्तरां का अनुमान है कि आने वाले सप्ताह के लिए उसकी कुल बिक्री न्यूनतम $10,000, अधिकतम $30,000 और संभवतः $25,000 होगी।

क्या संभावना है कि रेस्तरां की कुल बिक्री $20,000 से कम हो?
इस प्रश्न का उत्तर देने के लिए, हम x = कुल बिक्री पूछ सकते हैं। हम जानते हैं कि x $10,000 के न्यूनतम मान a और $25,000 के अधिकतम मान c के बीच स्थित है।
तो, पीडीएफ के अनुसार, हम इस संभावना को खोजने के लिए निम्नलिखित समीकरण का उपयोग कर सकते हैं कि रेस्तरां की कुल बिक्री $20,000 से कम है:
- पी(एक्स <$20,000) = (एक्सए) 2 / ((बीए)(सीए))
- पी(एक्स <$20,000) = (20,000-10,000) 2 / ((30,000-10,000)(25,000-10,000))
- पी(एक्स <$20,000) = 0.333
रेस्तरां की कुल बिक्री $20,000 से कम होने की संभावना 0.333 है।
रेस्तरां के लिए औसत अपेक्षित बिक्री क्या है?
हम पहले दिए गए औसत के सूत्र का उपयोग करके अपेक्षित औसत बिक्री की गणना कर सकते हैं:
- औसत = (ए + बी + सी) / 3
- औसत = ($10,000 + $30,000 + $25,000) / 3
- औसत = $21,667
औसत अपेक्षित बिक्री 21,667 है।
अतिरिक्त संसाधन
निम्नलिखित ट्यूटोरियल अन्य आमतौर पर उपयोग किए जाने वाले वितरणों का परिचय प्रदान करते हैं: