पायथन में द्विघात प्रतिगमन कैसे करें

द्विघात प्रतिगमन एक प्रकार का प्रतिगमन है जिसका उपयोग हम एक भविष्यवक्ता चर और एक प्रतिक्रिया चर के बीच संबंध को मापने के लिए कर सकते हैं जब वास्तविक संबंध द्विघात होते हैं, जो ग्राफ़ पर “यू” या उलटा “यू” जैसा दिख सकता है।

अर्थात्, जैसे-जैसे भविष्यवक्ता चर बढ़ता है, प्रतिक्रिया चर भी बढ़ता जाता है, लेकिन एक निश्चित बिंदु के बाद प्रतिक्रिया चर कम होने लगता है क्योंकि भविष्यवक्ता चर बढ़ता रहता है।

यह ट्यूटोरियल बताता है कि पायथन में द्विघात प्रतिगमन कैसे करें।

उदाहरण: पायथन में द्विघात प्रतिगमन

मान लीजिए कि हमारे पास 16 अलग-अलग लोगों के लिए प्रति सप्ताह काम किए गए घंटों की संख्या और खुशी के रिपोर्ट किए गए स्तर (0 से 100 के पैमाने पर) का डेटा है:

 import numpy as np
import scipy.stats as stats

#define variables
hours = [6, 9, 12, 12, 15, 21, 24, 24, 27, 30, 36, 39, 45, 48, 57, 60]
happ = [12, 18, 30, 42, 48, 78, 90, 96, 96, 90, 84, 78, 66, 54, 36, 24]

यदि हम इस डेटा का एक सरल स्कैटर प्लॉट बनाते हैं, तो हम देख सकते हैं कि दो चर के बीच का संबंध “यू” आकार का है:

 import matplotlib.pyplot as plt

#create scatterplot
plt.scatter(hours, happ) 

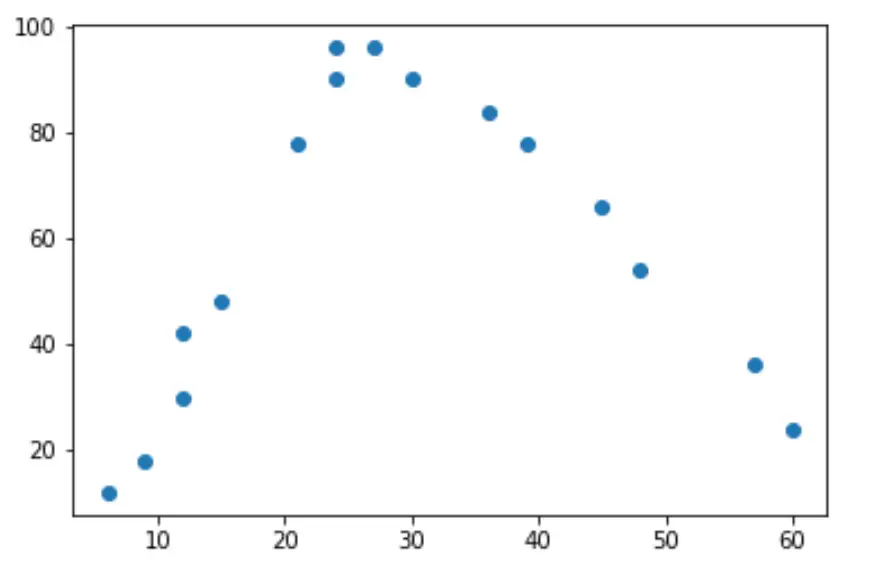
जैसे-जैसे काम के घंटे बढ़ते हैं, खुशी भी बढ़ती है, लेकिन जब काम के घंटे प्रति सप्ताह लगभग 35 घंटे से अधिक हो जाते हैं, तो खुशी कम होने लगती है।

इस “यू” आकार के कारण, इसका मतलब है कि द्विघात प्रतिगमन संभवतः दो चर के बीच संबंध को मापने के लिए एक अच्छा उम्मीदवार है।

वास्तव में एक द्विघात प्रतिगमन करने के लिए, हम numpy.polyfit() फ़ंक्शन का उपयोग करके 2 की डिग्री के साथ एक बहुपद प्रतिगमन मॉडल को फिट कर सकते हैं:

 import numpy as np

#polynomial fit with degree = 2
model = np.poly1d(np.polyfit(hours, happ, 2))

#add fitted polynomial line to scatterplot
polyline = np.linspace(1, 60, 50)
plt.scatter(hours, happ)
plt.plot(polyline, model(polyline))
plt.show() 

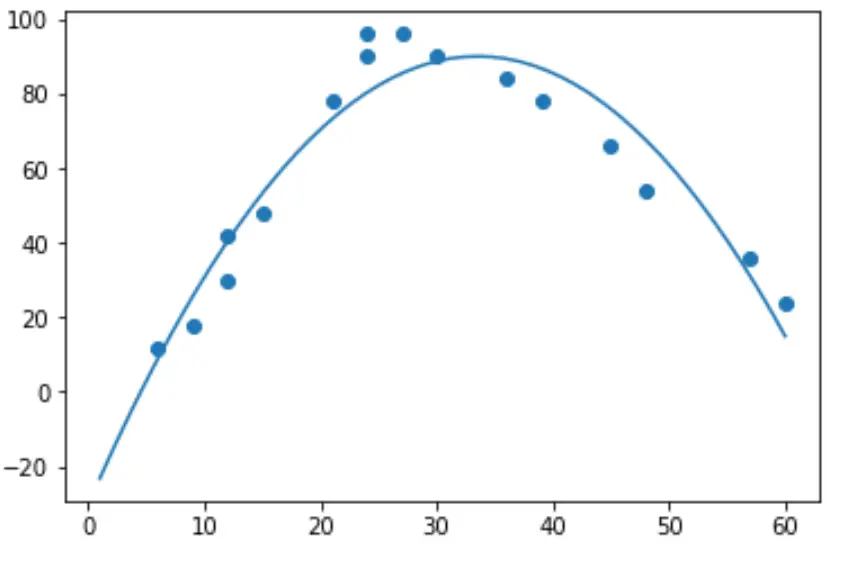
हम मॉडल गुणांकों को प्रिंट करके फिट किए गए बहुपद प्रतिगमन समीकरण प्राप्त कर सकते हैं:

 print (model)

-0.107x 2 + 7.173x - 30.25

फिट किया गया द्विघात प्रतिगमन समीकरण है:

ख़ुशी = -0.107(घंटे) ² + 7.173(घंटे) – 30.25

हम इस समीकरण का उपयोग किसी व्यक्ति के काम किए गए घंटों के आधार पर उसकी खुशी के अपेक्षित स्तर की गणना करने के लिए कर सकते हैं। उदाहरण के लिए, प्रति सप्ताह 30 घंटे काम करने वाले व्यक्ति की खुशी का अपेक्षित स्तर है:

खुशी = -0.107(30) ² + 7.173(30) – 30.25 = 88.64 ।

हम मॉडल का आर-वर्ग प्राप्त करने के लिए एक छोटा फ़ंक्शन भी लिख सकते हैं, जो प्रतिक्रिया चर में भिन्नता का अनुपात है जिसे भविष्यवक्ता चर द्वारा समझाया जा सकता है।

 #define function to calculate r-squared
def polyfit(x, y, degree):
    results = {}
    coeffs = np.polyfit(x, y, degree)
    p = np.poly1d(coeffs)
    #calculate r-squared
    yhat = p(x)
    ybar = np.sum(y)/len(y)
    ssreg = np.sum((yhat-ybar)**2)
    sstot = np.sum((y - ybar)**2)
    results['r_squared'] = ssreg / sstot

    return results

#find r-squared of polynomial model with degree = 3
polyfit(hours, happ, 2)

{'r_squared': 0.9092114182131691}

इस उदाहरण में, मॉडल का आर वर्ग 0.9092 है।

इसका मतलब यह है कि रिपोर्ट किए गए खुशी के स्तर में 90.92% भिन्नता को भविष्यवक्ता चर द्वारा समझाया जा सकता है।

अतिरिक्त संसाधन

पायथन में बहुपद प्रतिगमन कैसे करें
आर में द्विघात प्रतिगमन कैसे करें
एक्सेल में द्विघात प्रतिगमन कैसे करें