द्विपद वितरण के आकार को समझना

द्विपद वितरण n द्विपद प्रयोगों में k सफलताएँ प्राप्त करने की संभावना का वर्णन करता है।

यदि एक यादृच्छिक चर X एक द्विपद वितरण का अनुसरण करता है, तो संभावना है कि X = k की सफलता निम्नलिखित सूत्र द्वारा पाई जा सकती है:

पी(एक्स=के) = _एन सी _के * पी ^के * (1-पी) ^एनके

सोना:

• n: परीक्षणों की संख्या
• k: सफलताओं की संख्या
• पी: किसी दिए गए परीक्षण पर सफलता की संभावना
• _n C _k : n परीक्षणों में k सफलताएँ प्राप्त करने के तरीकों की संख्या

निम्नलिखित दो स्थितियों में से एक या अधिक होने पर द्विपद संभाव्यता वितरण घंटी के आकार का हो जाता है:

1. नमूना आकार (n) बड़ा है।

2. किसी दिए गए परीक्षण की सफलता की संभावना (पी) 0.5 के करीब है।

हालाँकि, जब इनमें से कोई भी स्थिति नहीं होती है तो द्विपद संभाव्यता वितरण विषम हो जाता है। इसे स्पष्ट करने के लिए, निम्नलिखित उदाहरणों पर विचार करें:

उदाहरण 1: नमूना आकार (एन) बड़ा है

निम्नलिखित ग्राफ n = 200 और p = 0.5 होने पर संभाव्यता वितरण प्रदर्शित करता है।

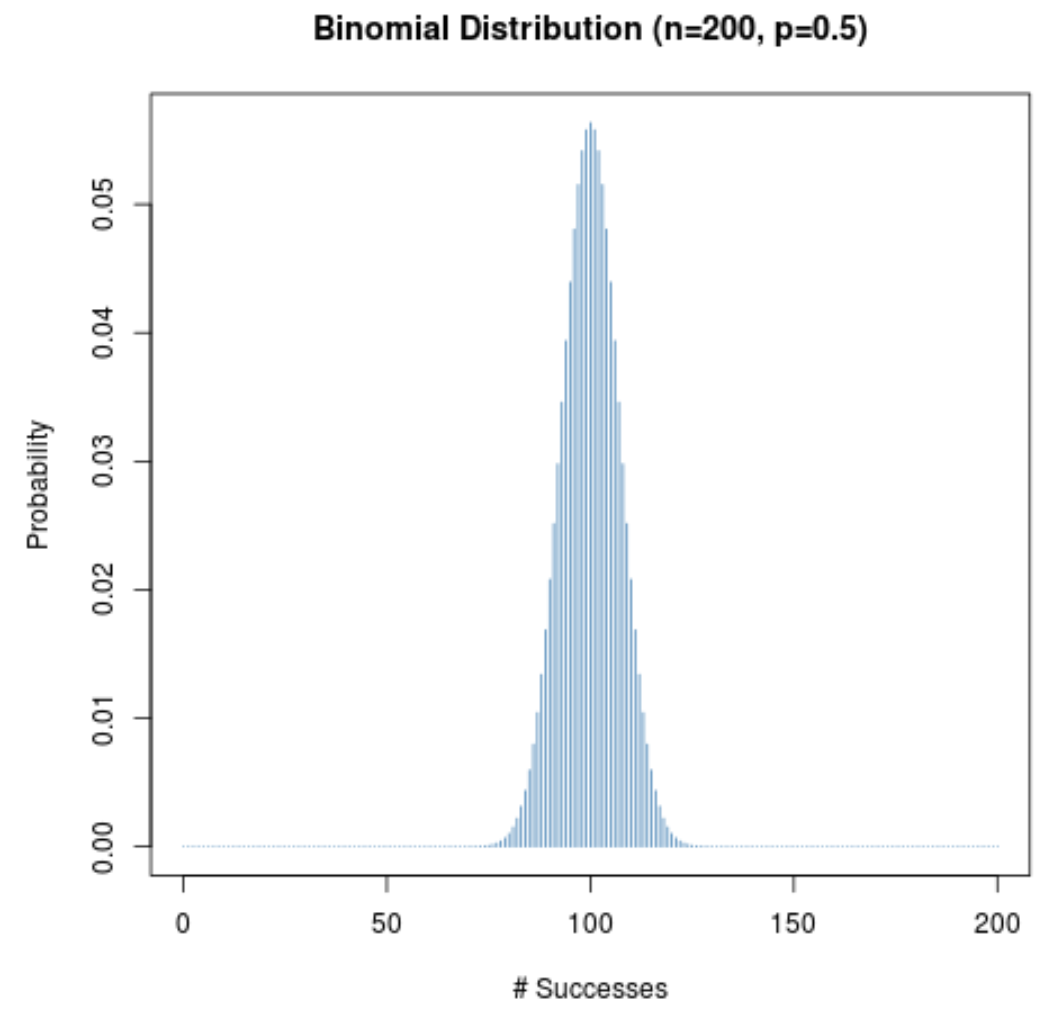
x-अक्ष 200 से अधिक परीक्षणों की सफलताओं की संख्या प्रदर्शित करता है और y-अक्ष उस संख्या की सफलताओं की संभावना प्रदर्शित करता है।

चूँकि (1) नमूना आकार बड़ा है और (2) किसी दिए गए परीक्षण की सफलता की संभावना 0.5 के करीब है, संभावना वितरण घंटी के आकार का है।

यहां तक कि जब किसी दिए गए परीक्षण (पी) की सफलता की संभावना 0.5 के करीब नहीं है, तब तक संभावना वितरण घंटी के आकार का रहेगा जब तक नमूना आकार (एन) बड़ा है। इसे स्पष्ट करने के लिए, निम्नलिखित दो परिदृश्यों पर विचार करें जब p = 0.2 और p = 0.8।

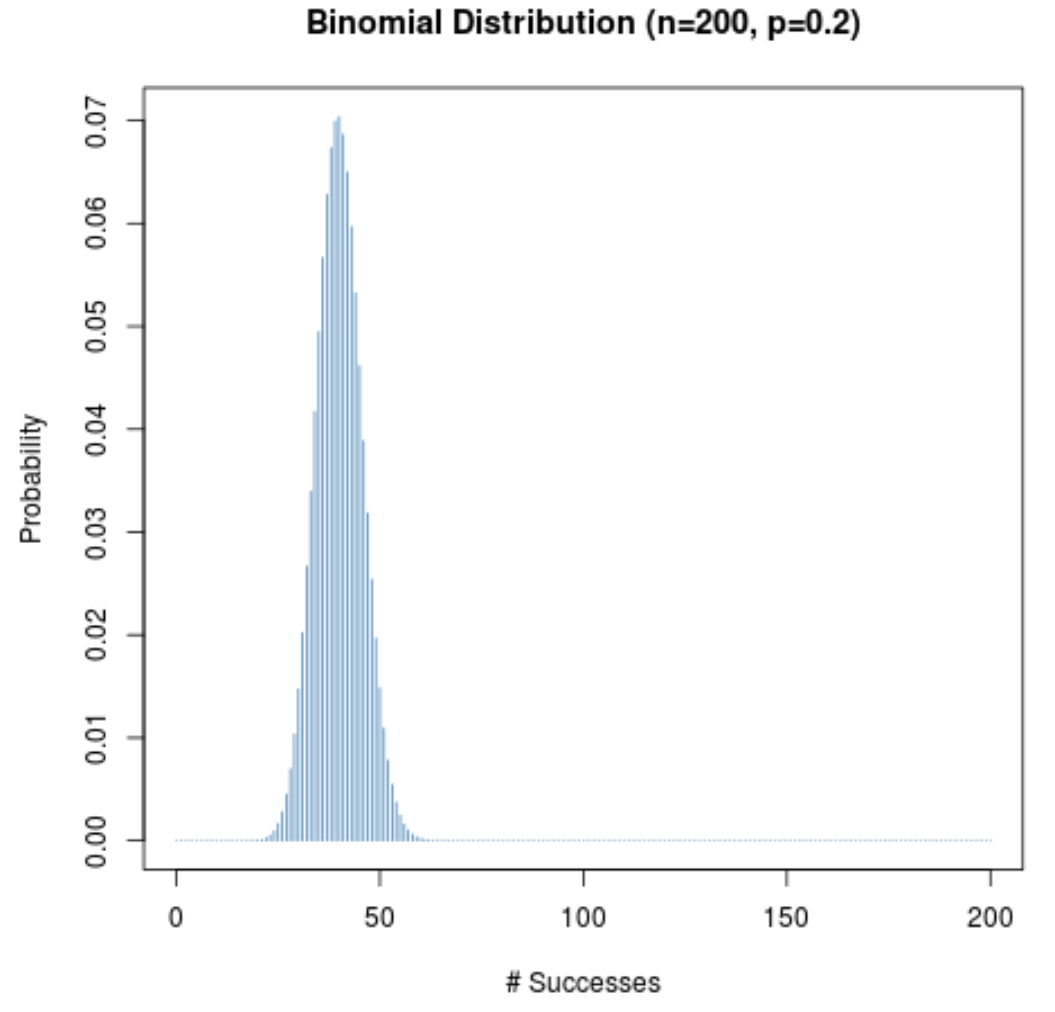
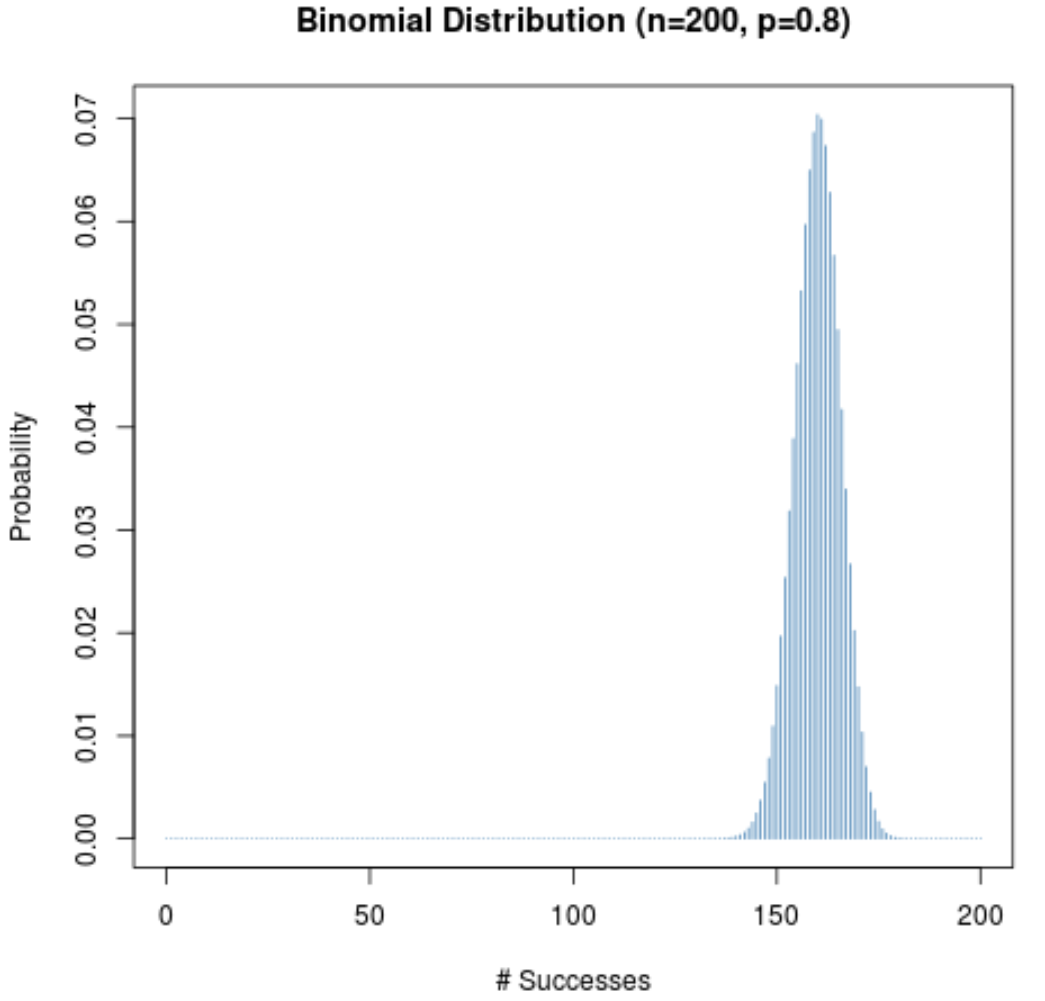
ध्यान दें कि दोनों परिदृश्यों में संभाव्यता वितरण घंटी के आकार का कैसे है।

उदाहरण 2: सफलता की संभावना (पी) 0.5 के करीब है

निम्नलिखित ग्राफ n = 10 और p = 0.4 होने पर संभाव्यता वितरण प्रदर्शित करता है।

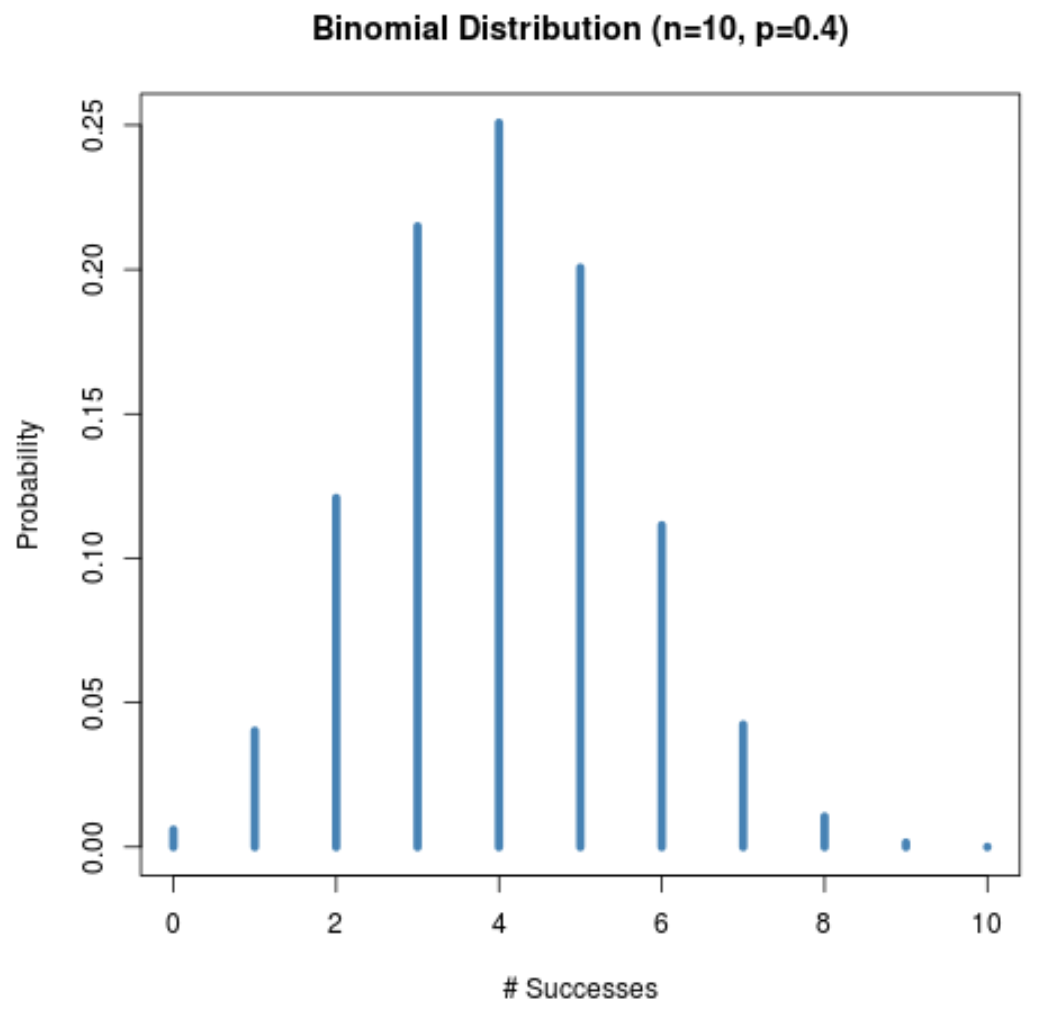
यद्यपि नमूना आकार (एन = 10) छोटा है, संभाव्यता वितरण घंटी के आकार का रहता है क्योंकि किसी दिए गए परीक्षण (पी = 0.4) की सफलता की संभावना 0.5 के करीब है।

उदाहरण 3: विषम द्विपद बंटन

जब न तो (1) नमूना आकार बड़ा है और न ही (2) किसी दिए गए परीक्षण की सफलता की संभावना 0.5 के करीब है, तो द्विपद संभाव्यता वितरण बाईं या दाईं ओर तिरछा हो जाएगा।

उदाहरण के लिए, निम्नलिखित ग्राफ n = 20 और p = 0.1 होने पर संभाव्यता वितरण दिखाता है।

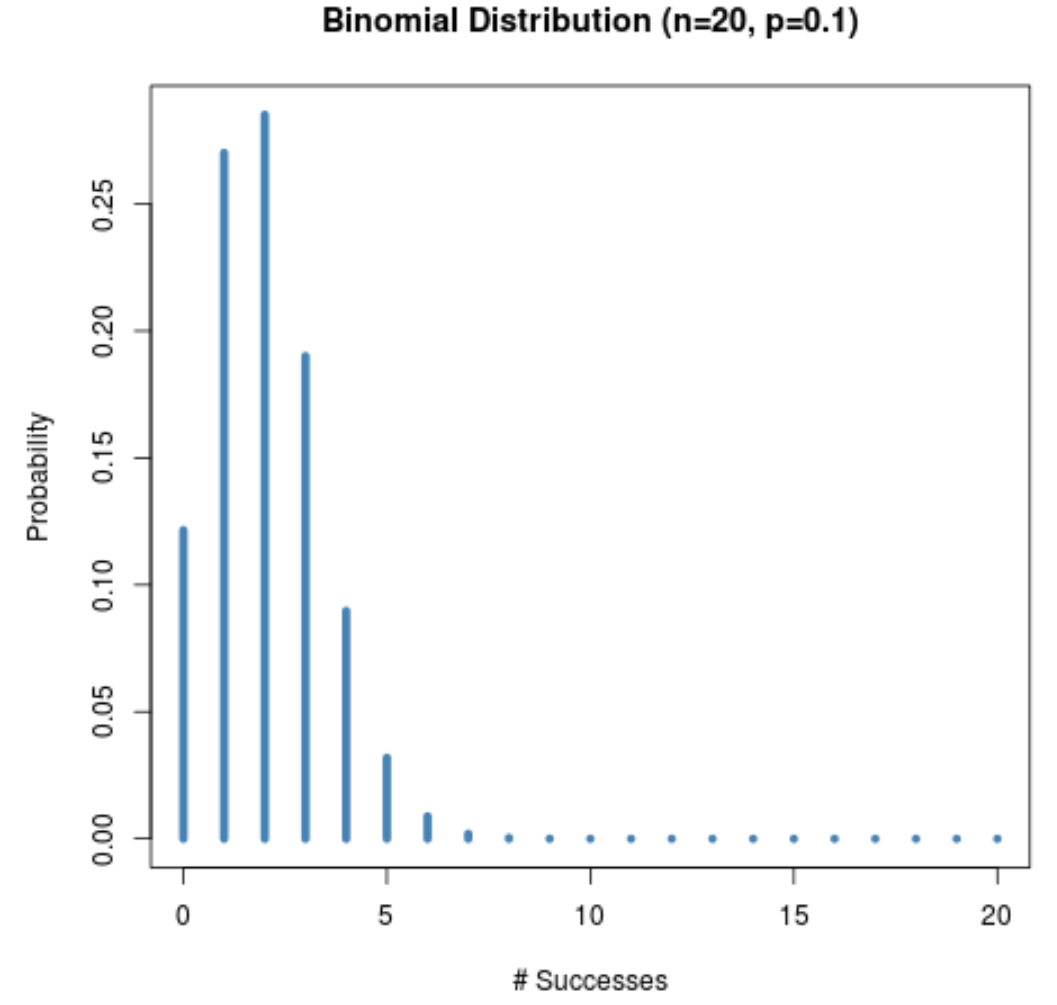
ध्यान दें कि वितरण दाईं ओर कैसे तिरछा है।

और निम्नलिखित ग्राफ n = 20 और p = 0.9 होने पर संभाव्यता वितरण दिखाता है।

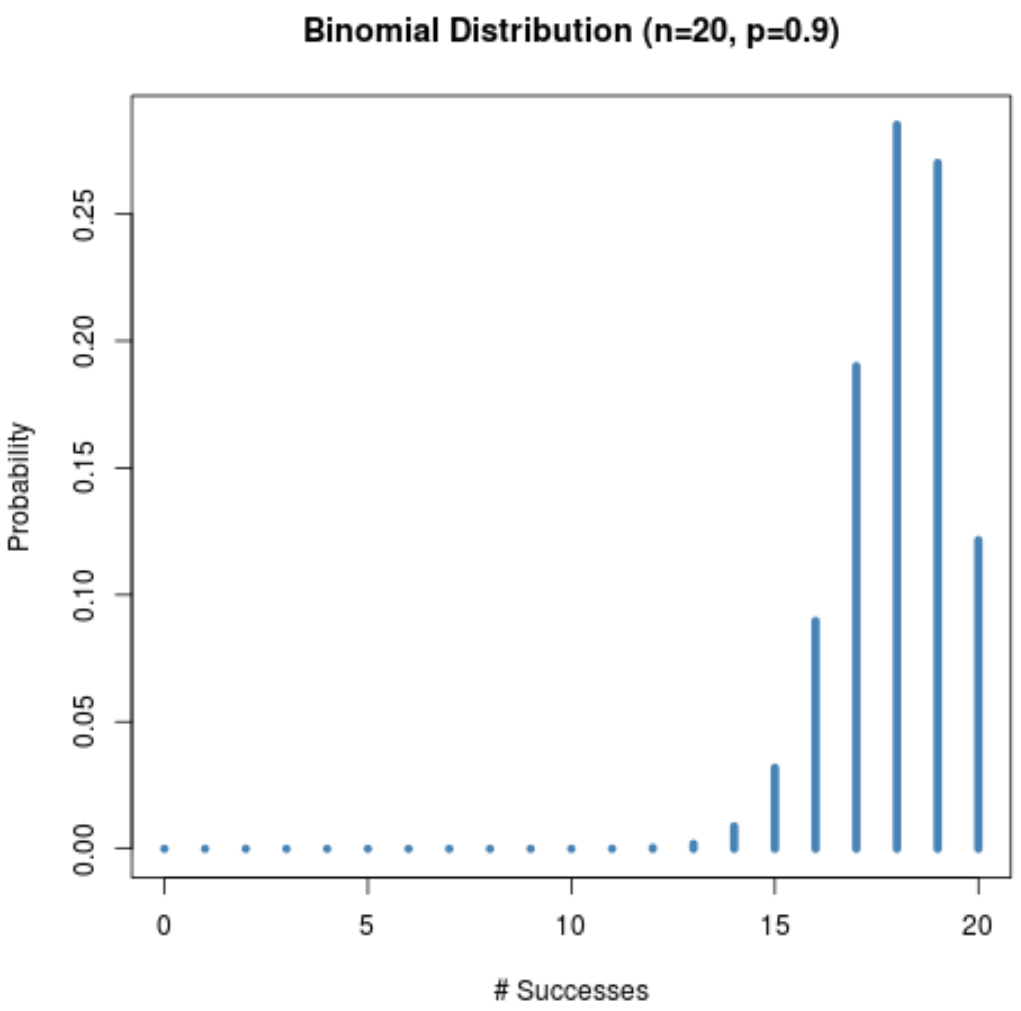
ध्यान दें कि वितरण बाईं ओर कैसे तिरछा है।

एंडनोट्स

इस आलेख में प्रत्येक ग्राफ़ आर सांख्यिकीय प्रोग्रामिंग भाषा का उपयोग करके बनाया गया था। इस ट्यूटोरियल का उपयोग करके आर में अपने स्वयं के द्विपद संभाव्यता वितरण को प्लॉट करना सीखें।