नमूने का आकार

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 3, 2023 आंकड़े शून्य टिप्पणियां

यह आलेख बताता है कि नमूना आकार क्या है और आंकड़ों में यह क्यों महत्वपूर्ण है। इसके अतिरिक्त, आप जानेंगे कि उचित नमूना आकार की गणना कैसे करें और एक हल किया गया अभ्यास ताकि आप देख सकें कि यह कैसे किया जाता है।

नमूना आकार क्या है?

नमूना आकार (या नमूना आकार ) उन व्यक्तियों की संख्या है जो अध्ययन का नमूना बनाते हैं। आंकड़ों में, नमूना आकार महत्वपूर्ण है ताकि नमूना संपूर्ण जनसंख्या का प्रतिनिधि हो।

इसलिए, एक सांख्यिकीय अध्ययन का नमूना आकार संपूर्ण जनसंख्या की विशेषताओं का प्रतिनिधित्व करने के लिए पर्याप्त बड़ा होना चाहिए। दूसरी ओर, नमूने का आकार अत्यधिक बड़ा नहीं हो सकता, क्योंकि तब शोध अधिक महंगा हो जाता है। निष्कर्षतः, नमूना आकार पर्याप्त होना चाहिए, न तो बहुत बड़ा और न ही बहुत छोटा।

उदाहरण के लिए, यदि हम किसी देश की ऊंचाई का विश्लेषण करना चाहते हैं, तो हम उस देश के सभी निवासियों की ऊंचाई नहीं पूछ सकते, क्योंकि सर्वेक्षण में लंबा समय लगेगा और यह बहुत महंगा होगा। इसलिए यादृच्छिक नमूनाकरण करना और जनसंख्या के केवल प्रतिनिधि नमूने का साक्षात्कार करना आवश्यक है।

➤ देखें: नमूने के प्रकार

और हम उचित नमूना आकार कैसे जान सकते हैं? अगले भाग में, हम देखेंगे कि अनुसंधान आवश्यकताओं के आधार पर उचित नमूना आकार कैसे निर्धारित किया जाए।

नमूना आकार की गणना कैसे करें

माध्य का अनुमान लगाने के लिए, आवश्यक नमूना आकार Z _α/2 के वर्ग को मानक विचलन (σ) से गुणा करके वांछित त्रुटि मार्जिन (ई) से विभाजित करने के बराबर है। इसलिए नमूना आकार की गणना करने का सूत्र है:

$\displaystyle n=\left(\frac{Z_{\alpha/2}\cdot\sigma}{e}\right)^2$

सोना:

$n$

नमूना आकार है.
$\alpha$

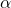
महत्व का वांछित स्तर है. इस बात को ध्यान में रखते हुए

$1-\alpha$

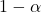
वांछित आत्मविश्वास स्तर है.
$Z_{\alpha/2}$

α/2 की संभावना के अनुरूप मानक सामान्य वितरण की मात्रा है। बड़े नमूना आकार और 95% आत्मविश्वास स्तर के लिए यह आमतौर पर 1.96 के करीब है और 99% आत्मविश्वास स्तर के लिए यह आमतौर पर 2.576 के करीब है।
$\sigma$

मानक विचलन है.

ध्यान रखें कि इस सूत्र में यह माना गया है कि जनसंख्या का आकार अनंत है, अर्थात जनसंख्या का आकार बहुत बड़ा या अज्ञात है।

नोट: उपरोक्त सूत्र माध्य के लिए विश्वास सूत्र अंतराल से लिया गया है।

नमूना आकार गणना का उदाहरण

इस अनुभाग में, हम एक उदाहरण के रूप में सांख्यिकीय सर्वेक्षण के लिए उपयुक्त नमूना आकार की गणना करेंगे।

हम जानते हैं कि किसी जनसंख्या का मानक विचलन लगभग 15 है, लेकिन हम इसका माध्य नहीं जानते हैं, इसलिए हम माध्य का अनुमान लगाने के लिए एक अध्ययन करना चाहते हैं। यदि हम 95% के विश्वास स्तर के साथ ±2 की त्रुटि का मार्जिन चाहते हैं तो हमें किस नमूना आकार की आवश्यकता है?

जैसा कि हमने ऊपर देखा, नमूना आकार की गणना करने का सूत्र है:

$\displaystyle n=\left(\frac{Z_{\alpha/2}\cdot\sigma}{e}\right)^2$

इस मामले में, वांछित आत्मविश्वास स्तर 95% है, इसलिए संबंधित Z _α/2 मान 1.96 है।

$1-\alpha=0,95 \ \color{orange}\bm{\longrightarrow}\color{black} \ \alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}$

➤ देखें: आत्मविश्वास स्तर मूल्यों वाली तालिका

अंत में, अब जब हम जानते हैं कि सभी पैरामीटर कितने मूल्य के हैं, तो हम उनके मानों को सूत्र में प्रतिस्थापित करते हैं और नमूना आकार की गणना करते हैं:

$\begin{aligned}\displaystyle n&=\left(\frac{Z_{\alpha/2}\cdot\sigma}{e}\right)^2\\[2ex] n&=\left(\frac{1,96\cdot 15}{2}\right)^2\\[2ex] n&=216,09 \approx 217 \end{array}$

संक्षेप में, वांछित आवश्यकताओं के साथ जनसंख्या का अनुमान लगाने के लिए, हमें कम से कम 217 व्यक्तियों के नमूने की आवश्यकता है।

नमूना आकार, आत्मविश्वास का स्तर और त्रुटि की संभावना

आत्मविश्वास के स्तर और आवश्यक त्रुटि की संभावना के आधार पर, आवश्यक नमूना आकार अलग-अलग होगा। इस प्रकार, नमूना आकार, आत्मविश्वास स्तर और त्रुटि का मार्जिन निम्नानुसार संबंधित हैं:

नमूना आकार और आत्मविश्वास का स्तर सीधे आनुपातिक हैं। यानी आत्मविश्वास का स्तर बढ़ेगा तो सैंपल साइज भी बढ़ेगा.
नमूना आकार और त्रुटि की संभावना व्युत्क्रमानुपाती होती है। इसलिए, यदि त्रुटि की संभावना बढ़ती है, तो नमूना आकार कम हो जाएगा।
इसलिए, नमूना आकार बढ़ाने से आत्मविश्वास का स्तर बढ़ सकता है या त्रुटि की संभावना कम हो सकती है।

अन्य नमूना आकार सूत्र

अनुमानित किए जाने वाले पैरामीटर के आधार पर, आवश्यक नमूना आकार का सूत्र थोड़ा भिन्न होता है। इसलिए, इस अनुभाग में हम अन्य सूत्र देखेंगे जो कुछ विशेष मामलों में नमूना आकार की गणना करने के लिए उपयोगी हो सकते हैं।

किसी अनुपात का नमूना आकार

अनुपात (पी) का अनुमान लगाने के लिए आवश्यक नमूना आकार की गणना करने का सूत्र है:

$n=\cfrac{N\cdot Z_{\alpha/2}^2\cdot p\cdot (1-p)}{e^2\cdot (N-1)+Z_{\alpha/2}^2\cdot p\cdot (1-p)}$

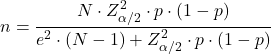
संभाव्यता का नमूना आकार

जब आप किसी संभाव्यता का अनुमान लगाना चाहते हैं, तो आवश्यक नमूना आकार निर्धारित करने के लिए निम्नलिखित सूत्र का उपयोग करने की अनुशंसा की जाती है:

$\displaystyle n=\left(\frac{Z_{\alpha/2}}{2\cdot e}\right)^2$

दो स्वतंत्र साधनों की तुलना के लिए नमूना आकार

किसी दिए गए α जोखिम और β जोखिम के साथ दो स्वतंत्र साधनों की तुलना करते समय नमूना आकार की गणना करने का सूत्र इस प्रकार है:

$n=\cfrac{2\cdot \sigma^2 \cdot \left(Z_{\alpha/2}+Z_\beta\right)}{\Delta^2}$

सोना

$\Delta$

वैकल्पिक परिकल्पना के दो साधनों के बीच का अंतर है।

दो युग्मित साधनों की तुलना के लिए नमूना आकार

यदि आप निश्चित त्रुटि α और त्रुटि β के साथ दो युग्मित साधनों की तुलना करना चाहते हैं, तो नमूने में अवलोकनों की संख्या ज्ञात करने के लिए उपयोग करने वाला सूत्र है:

$n=\cfrac{2\cdot \sigma_d^2 \cdot \left(Z_{\alpha/2}+Z_\beta\right)}{\Delta^2}$

सोना

$\Delta$

वैकल्पिक परिकल्पना के दो युग्मित साधनों के बीच का अंतर है और

$\sigma_d^2$

यह एक ही व्यक्ति के दो मापों के बीच अंतर का भिन्नता है।

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने