नमूना वितरण क्या है?

कल्पना कीजिए कि 10,000 डॉल्फ़िन की आबादी है और उस आबादी में एक डॉल्फ़िन का औसत वजन 300 पाउंड है।

यदि हम इस आबादी से 50 डॉल्फ़िन का एक सरल यादृच्छिक नमूना लेते हैं, तो हम पा सकते हैं कि इस नमूने में डॉल्फ़िन का औसत वजन 305 पाउंड है।

फिर, यदि हम 50 डॉल्फ़िन का एक और सरल यादृच्छिक नमूना लेते हैं, तो हम पा सकते हैं कि इस नमूने में डॉल्फ़िन का औसत वजन 295 पाउंड है।

जब भी हम 50 डॉल्फ़िन का एक साधारण यादृच्छिक नमूना लेते हैं, तो संभावना है कि नमूने में डॉल्फ़िन का औसत वजन जनसंख्या के औसत 300 पाउंड के करीब है, लेकिन बिल्कुल 300 पाउंड नहीं।

आइए कल्पना करें कि हम इस आबादी से 50 डॉल्फ़िन के 200 सरल यादृच्छिक नमूने लेते हैं और प्रत्येक नमूने के औसत वजन का एक हिस्टोग्राम बनाते हैं:

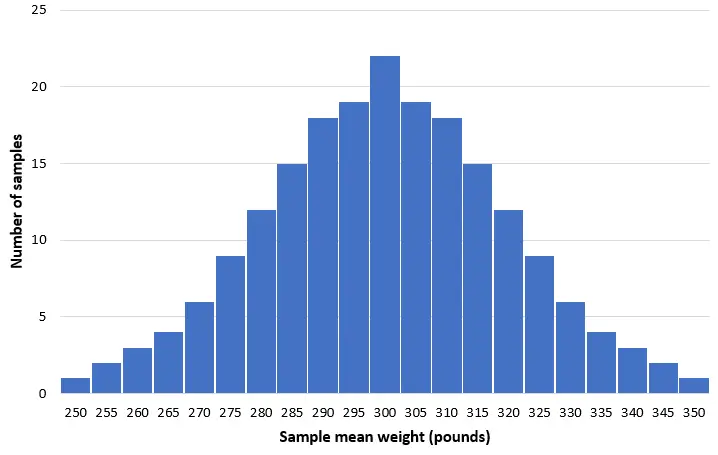
अधिकांश नमूनों में, औसत वजन 300 पाउंड के करीब होगा। दुर्लभ मामलों में, हम छोटी डॉल्फ़िन से भरा नमूना ले सकते हैं जिनका औसत वजन केवल 250 पाउंड है। या हम बॉटलनोज़ डॉल्फ़िन से भरा एक नमूना ले सकते हैं जिसका औसत वजन 350 पाउंड है। सामान्य तौर पर, नमूना साधनों का वितरण लगभग सामान्य होगा, वितरण का केंद्र जनसंख्या के वास्तविक केंद्र पर स्थित होगा।

नमूना माध्य के इस वितरण को माध्य के नमूना वितरण के रूप में जाना जाता है और इसमें निम्नलिखित गुण होते हैं:

_µx = µ

जहां μ _x नमूना माध्य है और μ जनसंख्या माध्य है।

_σx = σ/√n

जहां σ _x नमूना मानक विचलन है, σ जनसंख्या मानक विचलन है, और n नमूना आकार है।

उदाहरण के लिए, डॉल्फ़िन की इस आबादी में, हम जानते हैं कि औसत वजन μ = 300 है। इसलिए नमूना वितरण का माध्य μ _x = 300 है।

मान लीजिए कि हम यह भी जानते हैं कि जनसंख्या मानक विचलन 18 पाउंड है। इसलिए नमूना मानक विचलन σ _x = 18/ √50 = 2.546 है।

अनुपात का नमूना वितरण

10,000 डॉल्फ़िन की समान जनसंख्या पर विचार करें। मान लीजिए कि 10% डॉल्फ़िन काले हैं और बाकी भूरे हैं। मान लीजिए कि हम 50 डॉल्फ़िन का एक सरल यादृच्छिक नमूना लेते हैं और पाते हैं कि उस नमूने में 14% डॉल्फ़िन काली हैं। इसके बाद, हम 50 डॉल्फ़िन का एक और सरल यादृच्छिक नमूना लेते हैं और पाते हैं कि इस नमूने में 8% डॉल्फ़िन काली हैं।

कल्पना कीजिए कि हम इस आबादी से 50 डॉल्फ़िन के 200 सरल यादृच्छिक नमूने लेते हैं और प्रत्येक नमूने में काली डॉल्फ़िन के अनुपात का एक हिस्टोग्राम बनाते हैं:

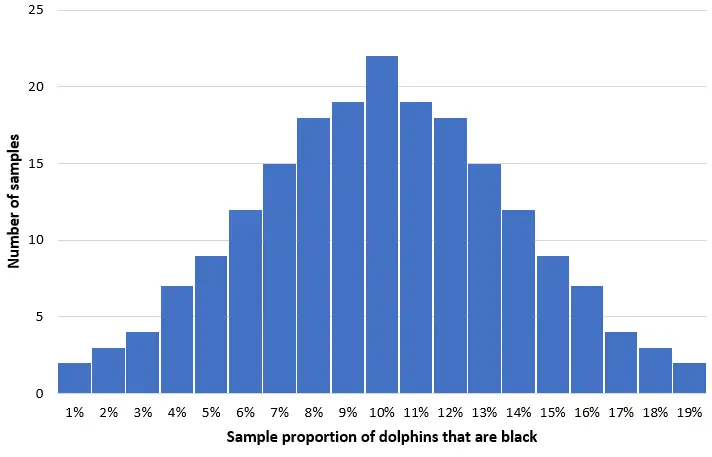
अधिकांश नमूनों में काली डॉल्फ़िन का अनुपात वास्तविक जनसंख्या 10% के करीब होगा। काली डॉल्फ़िन के नमूना अनुपात का वितरण लगभग सामान्य होगा, वितरण का केंद्र आबादी के वास्तविक केंद्र में स्थित होगा।

नमूना अनुपातों के इस वितरण को अनुपात के नमूना वितरण के रूप में जाना जाता है और इसमें निम्नलिखित गुण होते हैं:

_µp = पी

जहाँ p नमूना अनुपात है और P जनसंख्या अनुपात है।

σ _पी = √ (पी)(1-पी) / एन

जहां P जनसंख्या अनुपात है और n नमूना आकार है।

उदाहरण के लिए, इस डॉल्फ़िन आबादी में हम जानते हैं कि काली डॉल्फ़िन का वास्तविक अनुपात 10% = 0.1 है। इस प्रकार, आनुपातिक नमूना वितरण का माध्य μ _p = 0.1 है।

मान लीजिए कि हम यह भी जानते हैं कि जनसंख्या मानक विचलन 18 पाउंड है। इस प्रकार, नमूना मानक विचलन σ _p = √ (P)(1-P) / n = √ (.1)(1-.1) / 50 = .042 है।

सामान्य स्थिति स्थापित करें

उपरोक्त सूत्रों का उपयोग करने के लिए, नमूना वितरण सामान्य होना चाहिए।

केंद्रीय सीमा प्रमेय के अनुसार, यदि नमूना आकार काफी बड़ा है, तो नमूना माध्य का नमूना वितरण लगभग सामान्य है, भले ही जनसंख्या वितरण सामान्य न हो । ज्यादातर मामलों में, हम 30 या उससे अधिक के नमूना आकार को काफी बड़ा मानते हैं।

यदि सफलताओं और असफलताओं की अपेक्षित संख्या कम से कम 10 है तो नमूना अनुपात का नमूना वितरण लगभग सामान्य है।

उदाहरण

संभावनाओं की गणना के लिए हम नमूना वितरण का उपयोग कर सकते हैं।

उदाहरण 1: एक निश्चित मशीन कुकीज़ बनाती है। इन कुकीज़ का वजन वितरण 10 औंस के माध्य और 2 औंस के मानक विचलन के साथ दाईं ओर झुका हुआ है। यदि हम इस मशीन द्वारा उत्पादित 100 कुकीज़ का एक सरल यादृच्छिक नमूना लेते हैं, तो क्या संभावना है कि इस नमूने में कुकीज़ का औसत वजन 9.8 औंस से कम है?

चरण 1: सामान्य स्थिति स्थापित करें।

हमें यह सुनिश्चित करने की आवश्यकता है कि नमूना साधनों का नमूना वितरण सामान्य है। चूँकि हमारा नमूना आकार 30 से अधिक या उसके बराबर है, केंद्रीय सीमा प्रमेय के अनुसार, हम मान सकते हैं कि नमूना साधनों का नमूना वितरण सामान्य है।

चरण 2: नमूना वितरण का माध्य और मानक विचलन ज्ञात करें।

_µx = µ

_σx = σ/√n

_μx = 10 औंस

σ _x = 2/ √100 = 2/10 = 0.2 औंस

चरण 3: इस नमूने में औसत कुकी वजन 9.8 औंस से कम होने की संभावना निर्धारित करने के लिए जेड-स्कोर एरिया कैलकुलेटर का उपयोग करें।

Z स्कोर क्षेत्र कैलकुलेटर में निम्नलिखित संख्याएँ दर्ज करें। आप “रॉ स्कोर 2” को खाली छोड़ सकते हैं क्योंकि इस उदाहरण में हमें केवल एक नंबर मिलता है।

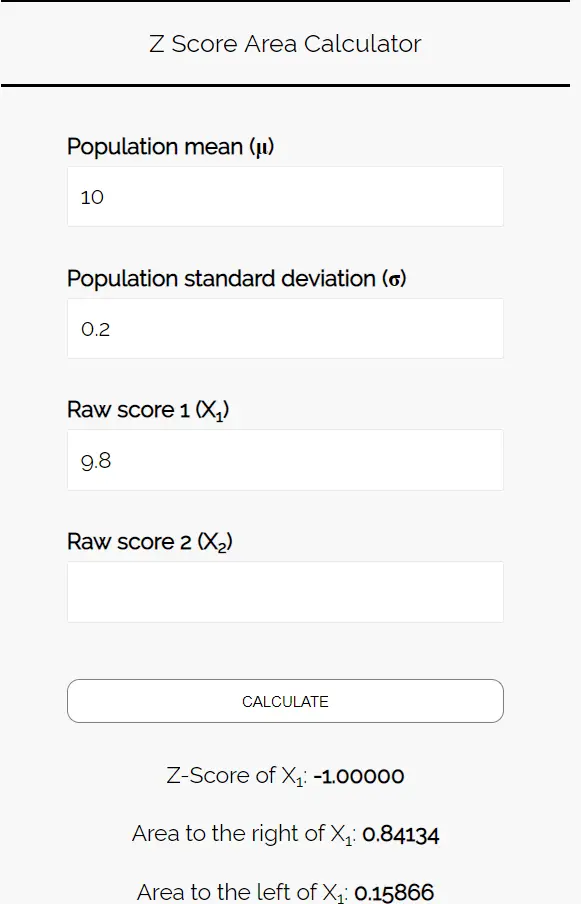
चूँकि हम इस संभावना को जानना चाहते हैं कि इस नमूने में कुकीज़ का औसत वजन 9.8 औंस से कम है, हम 9.8 के बाईं ओर के क्षेत्र में रुचि रखते हैं। कैलकुलेटर हमें बताता है कि यह संभावना 0.15866 है।

उदाहरण 2: एक स्कूल-व्यापी अध्ययन के अनुसार, एक विशेष स्कूल में 87% छात्र आइसक्रीम की तुलना में पिज़्ज़ा पसंद करते हैं। मान लीजिए हम 200 छात्रों का एक सरल यादृच्छिक नमूना लेते हैं। इसकी क्या प्रायिकता है कि पिज़्ज़ा पसंद करने वाले विद्यार्थियों का अनुपात 85% से कम है?

चरण 1: सामान्य स्थिति स्थापित करें।

याद रखें कि यदि “सफलताओं” और “असफलताओं” दोनों की अपेक्षित संख्या कम से कम 10 है, तो नमूना अनुपात का नमूना वितरण लगभग सामान्य है।

इस मामले में, पिज़्ज़ा पसंद करने वाले छात्रों की अपेक्षित संख्या 87% * 200 छात्र = 174 छात्र है। पिज़्ज़ा पसंद नहीं करने वाले छात्रों की अपेक्षित संख्या 13% * 200 छात्र = 26 छात्र है। चूँकि ये दोनों संख्याएँ कम से कम 10 हैं, हम मान सकते हैं कि पिज़्ज़ा पसंद करने वाले छात्रों के अनुपात का नमूना वितरण लगभग सामान्य है।

चरण 2: नमूना वितरण का माध्य और मानक विचलन ज्ञात करें।

_µp = पी

σ _पी = √ (पी)(1-पी) / एन

_µp = 0.87

σ _पी = √ (0.87)(1-0.87) / 200 = 0.024

चरण 3: इस संभावना को निर्धारित करने के लिए जेड-स्कोर एरिया कैलकुलेटर का उपयोग करें कि पिज्जा पसंद करने वाले छात्रों का अनुपात 85% से कम है।

Z स्कोर क्षेत्र कैलकुलेटर में निम्नलिखित संख्याएँ दर्ज करें। आप “रॉ स्कोर 2” को खाली छोड़ सकते हैं क्योंकि इस उदाहरण में हमें केवल एक नंबर मिलता है।

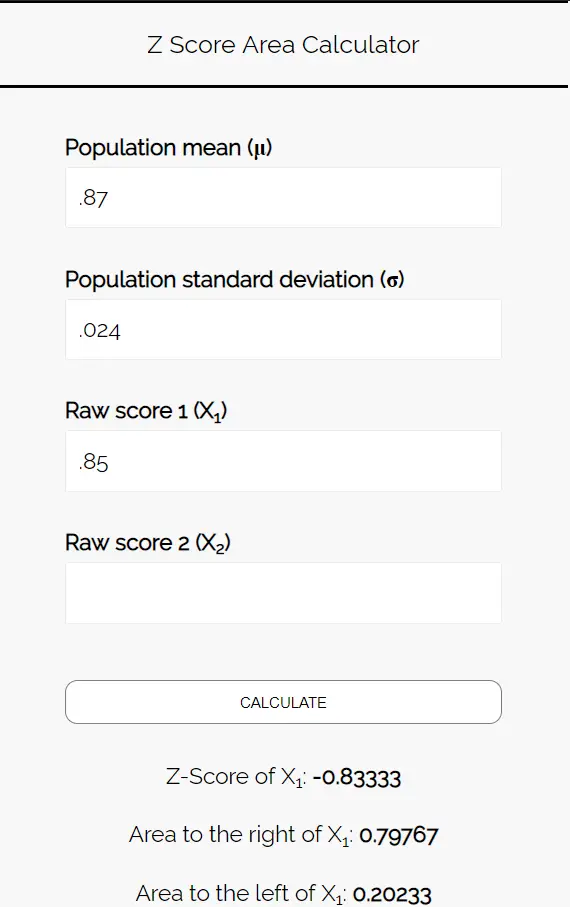
चूँकि हम इस संभावना को जानना चाहते हैं कि पिज़्ज़ा पसंद करने वाले छात्रों का अनुपात 85% से कम है, हम 0.85 के बाईं ओर के क्षेत्र में रुचि रखते हैं। कैलकुलेटर हमें बताता है कि यह संभावना 0.20233 है।