पियर्सन सहसंबंध गुणांक

पियर्सन सहसंबंध गुणांक (जिसे “उत्पाद-क्षण सहसंबंध गुणांक” के रूप में भी जाना जाता है) दो चर X और Y के बीच रैखिक संबंध का एक माप है। इसका मान -1 और 1 के बीच है जहां:

• -1 दो चरों के बीच पूर्णतः नकारात्मक रैखिक सहसंबंध दर्शाता है
• 0 दो चरों के बीच कोई रैखिक सहसंबंध नहीं दर्शाता है
• 1 दो चरों के बीच पूर्णतः सकारात्मक रैखिक सहसंबंध दर्शाता है

पियर्सन सहसंबंध गुणांक ज्ञात करने का सूत्र

डेटा के एक नमूने के लिए पियर्सन सहसंबंध गुणांक, जिसे r दर्शाया गया है, खोजने का सूत्र है ( विकिपीडिया के माध्यम से ):

आपको संभवतः इस सूत्र की गणना हाथ से कभी नहीं करनी पड़ेगी क्योंकि आप इसे करने के लिए सॉफ़्टवेयर का उपयोग कर सकते हैं, लेकिन एक उदाहरण के माध्यम से यह समझना उपयोगी है कि यह सूत्र वास्तव में क्या करता है।

मान लीजिए हमारे पास निम्नलिखित डेटा सेट है:

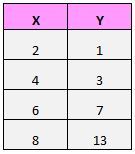
यदि हम इन जोड़ियों (X, Y) को स्कैटरप्लॉट पर प्लॉट करें, तो यह इस तरह दिखेगा:

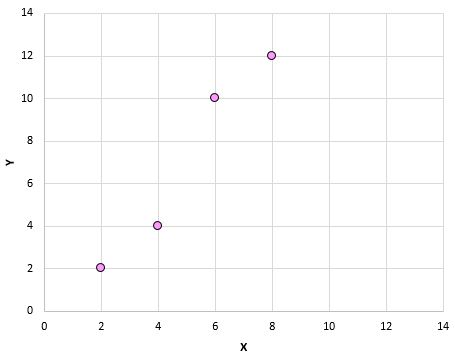
इस स्कैटरप्लॉट को देखकर, हम देख सकते हैं कि चर X और Y के बीच एक सकारात्मक संबंध है: जैसे-जैसे X बढ़ता है, Y भी बढ़ता जाता है। लेकिन यह निर्धारित करने के लिए कि ये दोनों चर कितने सकारात्मक रूप से जुड़े हुए हैं, हमें पियर्सन सहसंबंध गुणांक खोजने की आवश्यकता है।

आइए केवल सूत्र के अंश पर ध्यान दें:

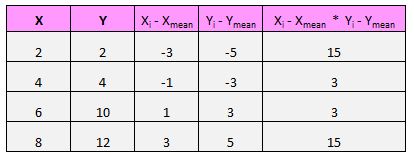
हमारे डेटासेट में प्रत्येक जोड़ी (X, Y) के लिए, हमें x मान और औसत x मान के बीच अंतर, y मान और औसत y मान के बीच अंतर ढूंढना होगा, और फिर इन दोनों संख्याओं को एक साथ गुणा करना होगा।

उदाहरण के लिए, हमारी पहली जोड़ी (X, Y) (2, 2) है। इस डेटा सेट में x का औसत मान 5 है और इस डेटा सेट में y का औसत मान 7 है। इसलिए इस जोड़ी के x मान और x के औसत मान के बीच का अंतर 2 – 5 = -3 है। इस जोड़ी के y मान और औसत y मान के बीच का अंतर 2 – 7 = -5 है। फिर जब हम इन दोनों संख्याओं को गुणा करते हैं तो हमें -3 * -5 = 15 प्राप्त होता है।

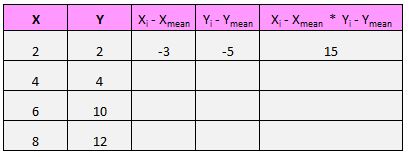
हमने अभी जो किया उसका एक दृश्य अवलोकन यहां दिया गया है:

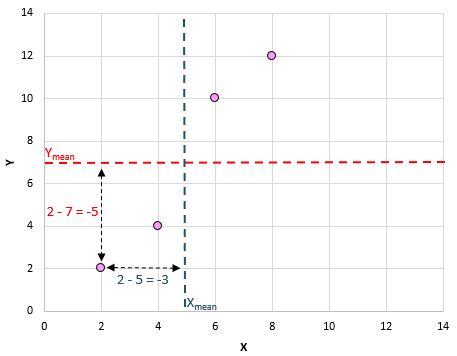
तो बस प्रत्येक जोड़ी के लिए यह करें:

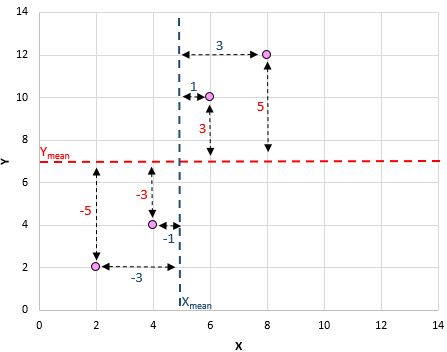
सूत्र का अंश प्राप्त करने का अंतिम चरण इन सभी मानों को एक साथ जोड़ना है:

15 + 3 +3 + 15 = 36

फिर सूत्र का हर हमें x और y के सभी वर्ग अंतरों का योग ज्ञात करने के लिए कहता है, फिर इन दोनों संख्याओं को एक साथ गुणा करें, फिर वर्गमूल निकालें:

तो सबसे पहले हम x और y के अंतरों के वर्गों का योग ज्ञात करेंगे:

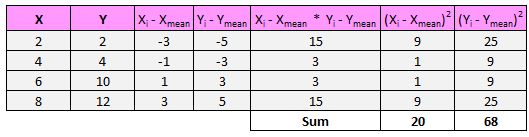
इसके बाद, हम इन दोनों संख्याओं को एक साथ गुणा करेंगे: 20 * 68 = 1,360.

अंत में, हम वर्गमूल लेंगे: √ 1,360 = 36.88

तो हमने पाया कि सूत्र का अंश 36 है और हर 36.88 है। इसका मतलब है कि हमारा पियर्सन सहसंबंध गुणांक r = 36 / 36.88 = 0.976 है

यह संख्या 1 के करीब है, जो दर्शाता है कि हमारे चर एक्स और वाई के बीच एक मजबूत सकारात्मक रैखिक संबंध है। यह उस रिश्ते की पुष्टि करता है जिसे हमने स्कैटरप्लॉट में देखा था।

सहसंबंध देखें

याद रखें कि पियर्सन सहसंबंध गुणांक हमें दो चरों के बीच रैखिक संबंध (सकारात्मक, नकारात्मक, कोई नहीं) के प्रकार के साथ-साथ इस रिश्ते की ताकत (कमजोर, मध्यम, मजबूत) बताता है।

जब हम दो वेरिएबल्स का स्कैटरप्लॉट बनाते हैं, तो हम दो वेरिएबल्स के बीच वास्तविक संबंध देख सकते हैं। यहां कई प्रकार के रैखिक संबंध हैं जिन्हें हम देख सकते हैं:

मजबूत, सकारात्मक संबंध: जैसे-जैसे x-अक्ष पर चर बढ़ता है, y-अक्ष पर चर भी बढ़ता है। बिंदुओं को बारीकी से एकत्रित किया गया है, जो एक मजबूत संबंध का संकेत देता है।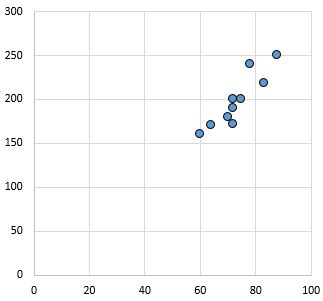

पियर्सन सहसंबंध गुणांक: 0.94

कमजोर और सकारात्मक संबंध: जैसे-जैसे x-अक्ष पर चर बढ़ता है, y-अक्ष पर चर भी बढ़ता है। बिंदु काफी बिखरे हुए हैं, जो कमजोर रिश्ते का संकेत दे रहे हैं।

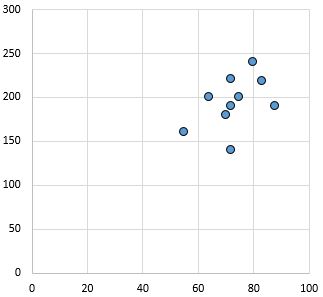
पियर्सन सहसंबंध गुणांक: 0.44

कोई संबंध नहीं: चरों के बीच कोई स्पष्ट संबंध (सकारात्मक या नकारात्मक) नहीं है।

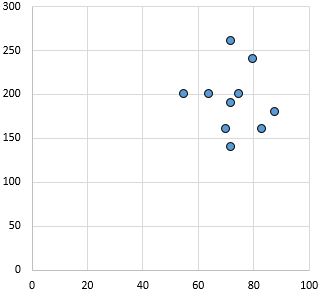
पियर्सन सहसंबंध गुणांक: 0.03

मजबूत, नकारात्मक संबंध: जैसे-जैसे x-अक्ष पर चर बढ़ता है, y-अक्ष पर चर घटता जाता है। बिंदुओं को कसकर एक साथ पैक किया गया है, जो एक मजबूत रिश्ते का संकेत देता है।

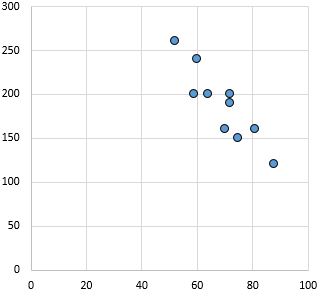
पियर्सन सहसंबंध गुणांक: -0.87

कमजोर और नकारात्मक संबंध: जैसे-जैसे x-अक्ष पर चर बढ़ता है, y-अक्ष पर चर घटता जाता है। बिंदु काफी बिखरे हुए हैं, जो कमजोर रिश्ते का संकेत दे रहे हैं।

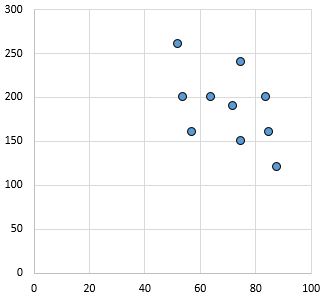
पियर्सन सहसंबंध गुणांक:- 0.46

पियर्सन सहसंबंध गुणांक के महत्व का परीक्षण

जब हम डेटा के एक सेट के लिए पियर्सन सहसंबंध गुणांक पाते हैं, तो हम अक्सर एक बड़ी आबादी के डेटा के नमूने के साथ काम कर रहे होते हैं। इसका मतलब यह है कि दो चर के लिए एक गैर-शून्य सहसंबंध खोजना संभव है, भले ही वे वास्तव में समग्र जनसंख्या में असंबद्ध हों।

उदाहरण के लिए, मान लीजिए कि हम संपूर्ण जनसंख्या में प्रत्येक डेटा बिंदु के लिए वेरिएबल X और Y के लिए एक स्कैटरप्लॉट बनाते हैं और यह इस तरह दिखता है:

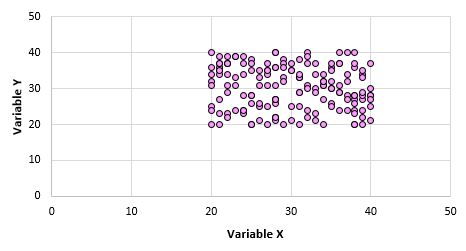
यह स्पष्ट है कि ये दोनों चर सहसंबद्ध नहीं हैं। हालाँकि, यह संभव है कि जब हम जनसंख्या से 10 बिंदुओं का नमूना लेते हैं, तो हम निम्नलिखित बिंदुओं को चुनते हैं:

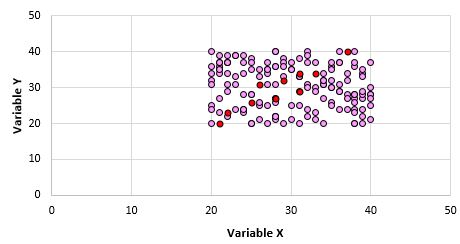
हम देख सकते हैं कि अंकों के इस नमूने के लिए पियर्सन सहसंबंध गुणांक 0.93 है, जो जनसंख्या सहसंबंध शून्य होने के बावजूद एक मजबूत सकारात्मक सहसंबंध दर्शाता है।

यह जांचने के लिए कि दो चरों के बीच सहसंबंध सांख्यिकीय रूप से महत्वपूर्ण है या नहीं, हम निम्नलिखित परीक्षण आँकड़े पा सकते हैं:

परीक्षण आँकड़ा टी = आर * √ (एन-2) / (1-आर ² )

जहां n हमारे नमूने में जोड़े की संख्या है, r पियर्सन सहसंबंध गुणांक है, और T परीक्षण आँकड़ा स्वतंत्रता की n-2 डिग्री के साथ एक वितरण का अनुसरण करता है।

आइए एक उदाहरण की समीक्षा करें कि पियर्सन सहसंबंध गुणांक के महत्व का परीक्षण कैसे करें।

उदाहरण

निम्नलिखित डेटासेट 12 व्यक्तियों की ऊंचाई और वजन दर्शाता है:

नीचे दिया गया स्कैटरप्लॉट इन दो चरों का मान दिखाता है:

इन दो चरों के लिए पियर्सन सहसंबंध गुणांक r = 0.836 है।

परीक्षण आँकड़ा टी = 0.836 * √ (12 -2) / (1-0.836 ² ) = 4.804।

हमारे टी वितरण कैलकुलेटर के अनुसार, 10 डिग्री स्वतंत्रता के साथ 4.804 के स्कोर का पी-मान 0.0007 है। चूँकि 0.0007 <0.05, हम यह निष्कर्ष निकाल सकते हैं कि इस उदाहरण में वजन और ऊंचाई के बीच संबंध अल्फा = 0.05 पर सांख्यिकीय रूप से महत्वपूर्ण है।

सावधानियां

हालाँकि पियर्सन सहसंबंध गुणांक हमें यह बताने में उपयोगी हो सकता है कि दो चरों में रैखिक संबंध है या नहीं, हमें पियर्सन सहसंबंध गुणांक की व्याख्या करते समय तीन बातों को ध्यान में रखना होगा:

1. सहसंबंध का अर्थ कार्य-कारण नहीं है। ऐसा इसलिए नहीं है क्योंकि दो चर सहसंबद्ध हैं, इसलिए एक आवश्यक रूप से दूसरे को कम या ज्यादा बार प्रकट होने का कारण बनता है । इसका एक उत्कृष्ट उदाहरण आइसक्रीम की बिक्री और शार्क के हमलों के बीच सकारात्मक संबंध है। जब साल के कुछ निश्चित समय में आइसक्रीम की बिक्री बढ़ती है, तो शार्क के हमले भी बढ़ जाते हैं।

क्या इसका मतलब यह है कि आइसक्रीम खाने से शार्क के हमले होते हैं ? बिल्कुल नहीं! इसका सीधा मतलब यह है कि गर्मियों में बर्फ की खपत और शार्क के हमले बढ़ जाते हैं, क्योंकि गर्मियों में बर्फ अधिक लोकप्रिय होती है और गर्मियों के दौरान अधिक लोग समुद्र में जाते हैं।

2. सहसंबंध बाह्य कारकों के प्रति संवेदनशील होते हैं। अत्यधिक बाह्यता पियर्सन सहसंबंध गुणांक को महत्वपूर्ण रूप से बदल सकती है। नीचे दिए गए उदाहरण पर विचार करें:

चर X और Y का पियर्सन सहसंबंध गुणांक 0.00 है। लेकिन कल्पना कीजिए कि हमारे पास डेटासेट में एक बाहरी चीज़ है:

हालाँकि, इन दो चरों के लिए पियर्सन सहसंबंध गुणांक 0.878 है। यह एक बाहरी चीज़ सब कुछ बदल देती है। यही कारण है कि, दो चर के लिए सहसंबंध की गणना करते समय, आउटलेर्स की जांच करने के लिए स्कैटरप्लॉट का उपयोग करके चर की कल्पना करना एक अच्छा विचार है।

3. पियर्सन सहसंबंध गुणांक दो चर के बीच गैर-रेखीय संबंधों को कैप्चर नहीं करता है। आइए कल्पना करें कि हमारे पास निम्नलिखित संबंध वाले दो चर हैं:

इन दो चरों के लिए पियर्सन सहसंबंध गुणांक 0.00 है क्योंकि उनका कोई रैखिक संबंध नहीं है। हालाँकि, इन दो चरों का एक गैर-रेखीय संबंध है: y मान केवल x मान का वर्ग है।

पियर्सन सहसंबंध गुणांक का उपयोग करते समय, ध्यान रखें कि आप केवल यह परीक्षण कर रहे हैं कि क्या दो चर रैखिक रूप से संबंधित हैं। भले ही पियर्सन सहसंबंध गुणांक हमें बताता है कि दो चर सहसंबद्ध नहीं हैं, फिर भी उनमें कुछ प्रकार के अरेखीय संबंध हो सकते हैं। यह एक और कारण है कि दो चर के बीच संबंधों का विश्लेषण करते समय एक स्कैटरप्लॉट बनाना उपयोगी होता है: यह आपको एक गैर-रेखीय संबंध का पता लगाने में मदद कर सकता है।