पियर्सन के सहसंबंध की पाँच परिकल्पनाएँ

पियर्सन सहसंबंध गुणांक (जिसे “उत्पाद-क्षण सहसंबंध गुणांक” के रूप में भी जाना जाता है) दो चर के बीच रैखिक संबंध को मापता है।

यह हमेशा -1 और 1 के बीच मान लेता है जहां:

• -1 दो चरों के बीच पूर्णतः नकारात्मक रैखिक सहसंबंध दर्शाता है
• 0 दो चरों के बीच कोई रैखिक सहसंबंध नहीं दर्शाता है
• 1 दो चरों के बीच पूर्णतः सकारात्मक रैखिक सहसंबंध दर्शाता है

हालाँकि, दो चरों के बीच पियर्सन सहसंबंध गुणांक की गणना करने से पहले, हमें यह सुनिश्चित करना होगा कि पाँच धारणाएँ पूरी हों:

1. माप का स्तर: दोनों चर को अंतराल या अनुपात स्तर पर मापा जाना चाहिए।

2. रैखिक संबंध: दो चरों के बीच एक रैखिक संबंध होना चाहिए।

3. सामान्यता: दोनों चरों का लगभग सामान्य वितरण होना चाहिए।

4. संबंधित जोड़े: डेटासेट में प्रत्येक अवलोकन में मानों की एक जोड़ी होनी चाहिए।

5. कोई आउटलेयर नहीं: डेटा सेट में कोई अत्यधिक आउटलेयर नहीं होना चाहिए।

इस लेख में, हम प्रत्येक धारणा का स्पष्टीकरण प्रदान करते हैं और साथ ही यह कैसे निर्धारित करें कि धारणा पूरी हुई है या नहीं।

परिकल्पना 1: माप का स्तर

दो चरों के बीच पियर्सन सहसंबंध गुणांक की गणना करने के लिए, दोनों चर को अंतराल या अनुपात स्तर पर मापा जाना चाहिए।

निम्नलिखित ग्राफ़िक उन चार स्तरों का त्वरित विवरण प्रदान करता है जिन पर चर को मापा जा सकता है:

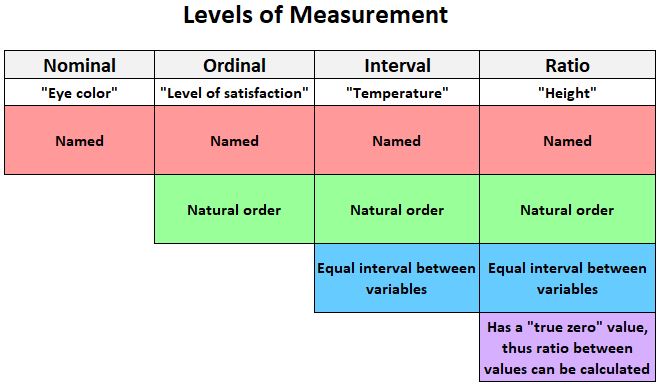
यहां चर के कुछ उदाहरण दिए गए हैं जिन्हें अंतराल पैमाने पर मापा जा सकता है:

• तापमान: फ़ारेनहाइट या सेल्सियस में मापा जाता है
• क्रेडिट स्कोर: 300 से 850 तक मापा गया
• SAT स्कोर: 400 से 1,600 तक मापा गया

यहां चरों के कुछ उदाहरण दिए गए हैं जिन्हें अनुपात पैमाने पर मापा जा सकता है:

• ऊंचाई: सेंटीमीटर, इंच, फुट आदि में मापी जाती है।
• वजन: किलोग्राम, पाउंड आदि में मापा जाता है।
• लंबाई: सेंटीमीटर, इंच, फुट आदि में मापी जाती है।

यदि चर को क्रमिक स्तर पर मापा जाता है, तो आपको उनके बीच स्पीयरमैन सहसंबंध गुणांक की गणना करने की आवश्यकता है।

संबंधित: माप के स्तर: नाममात्र, क्रमवाचक, अंतराल और अनुपात

परिकल्पना 2: रैखिक संबंध

दो चरों के बीच पियर्सन सहसंबंध गुणांक की गणना करने के लिए, दो चरों के बीच एक रैखिक संबंध होना चाहिए।

इस परिकल्पना का परीक्षण करने का सबसे आसान तरीका बस दो चर का एक स्कैटरप्लॉट बनाना है। यदि प्लॉट पर बिंदु लगभग एक सीधी रेखा का अनुसरण करते हैं, तो एक रैखिक संबंध मौजूद होता है:

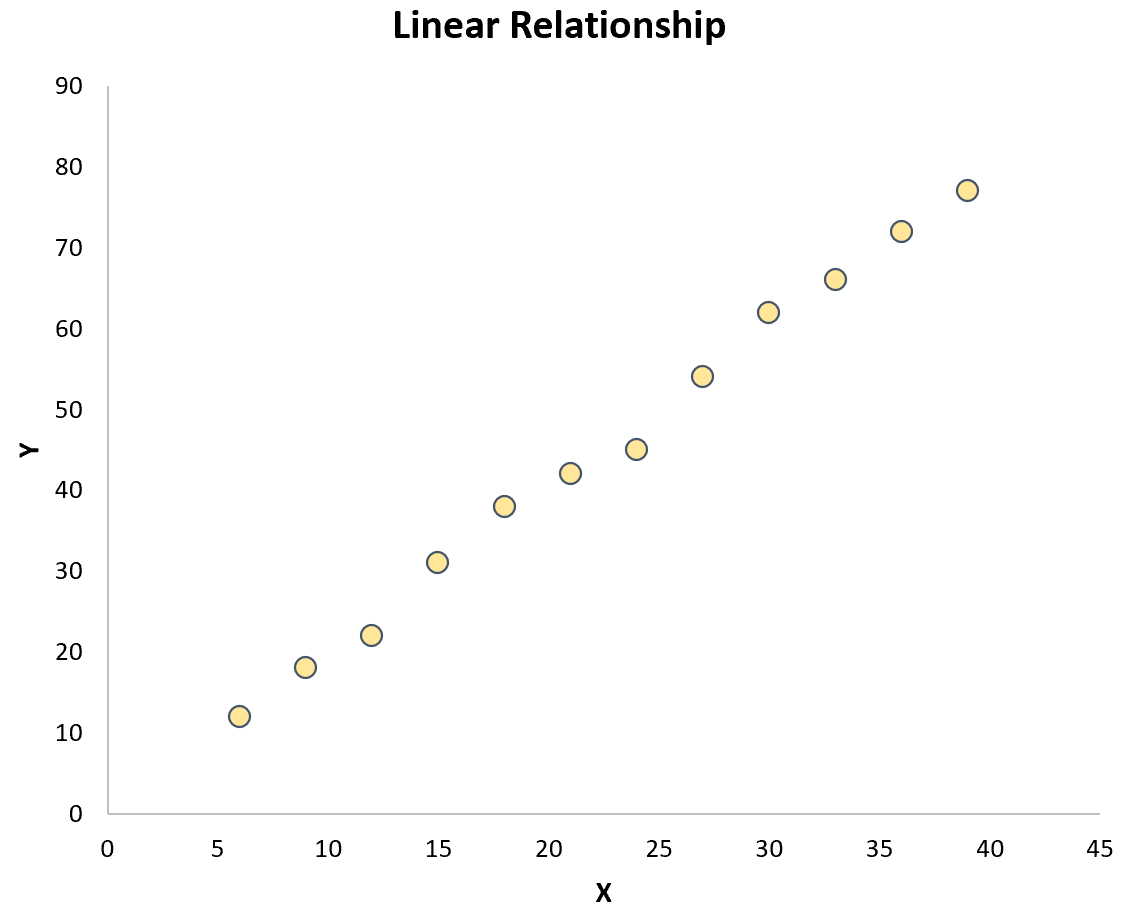
हालाँकि, यदि बिंदु पूरे कथानक में बेतरतीब ढंग से बिखरे हुए हैं या उनमें किसी अन्य प्रकार का संबंध है (जैसे कि द्विघात), तो चर के बीच एक रैखिक संबंध मौजूद नहीं है:

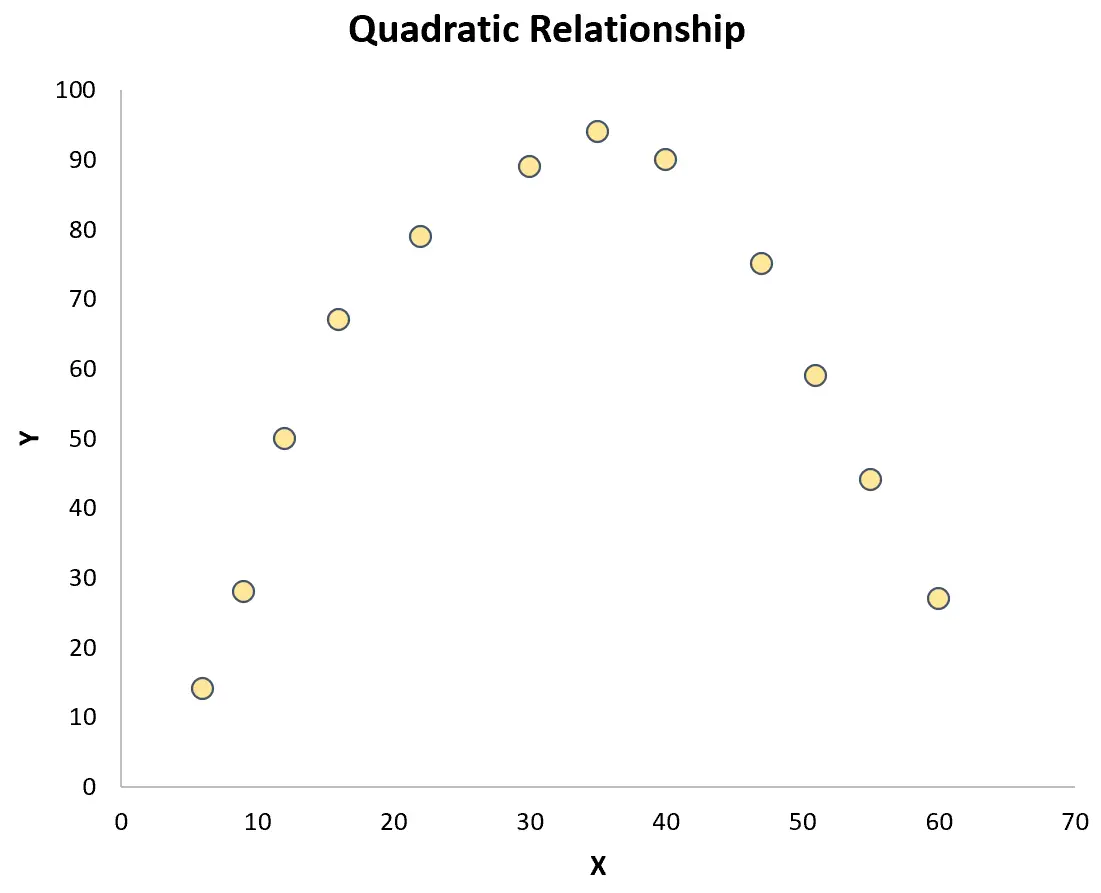
इस मामले में, पियर्सन सहसंबंध गुणांक चर के बीच संबंध को पर्याप्त रूप से कैप्चर नहीं करेगा।

परिकल्पना 3: सामान्यता

पियर्सन सहसंबंध गुणांक यह भी मानता है कि दो चर लगभग सामान्य रूप से वितरित हैं।

आप प्रत्येक चर के लिए हिस्टोग्राम या QQ प्लॉट बनाकर इस धारणा को दृष्टिगत रूप से सत्यापित कर सकते हैं।

1. हिस्टोग्राम

यदि डेटा सेट का हिस्टोग्राम मोटे तौर पर घंटी के आकार का है, तो यह संभावना है कि डेटा सामान्य रूप से वितरित किया जाता है।

2. क्यूक्यूलैंड

एक QQ प्लॉट, जिसका संक्षिप्त रूप “क्वांटाइल-क्वांटाइल” है, एक प्रकार का प्लॉट है जो x-अक्ष के साथ सैद्धांतिक क्वांटाइल प्रदर्शित करता है (यानी यदि आपका डेटा सामान्य वितरण का पालन करता है तो वह कहां होगा) और y-अक्ष के साथ नमूनों की मात्रा प्रदर्शित करता है। (यानी जहां आपका डेटा वास्तव में रहता है)।

यदि डेटा मान 45 डिग्री का कोण बनाते हुए लगभग सीधी रेखा का अनुसरण करते हैं, तो डेटा को सामान्य रूप से वितरित माना जाता है।

आप यह निर्धारित करने के लिए एक औपचारिक सांख्यिकीय परीक्षण भी कर सकते हैं कि कोई चर सामान्य रूप से वितरित है या नहीं।

यदि परीक्षण का पी-मान एक निश्चित स्तर के महत्व से नीचे है (जैसे कि α = 0.05), तो आपके पास यह कहने के लिए पर्याप्त सबूत हैं कि डेटा सामान्य रूप से वितरित नहीं है।

सामान्यता का परीक्षण करने के लिए आमतौर पर तीन सांख्यिकीय परीक्षण उपयोग किए जाते हैं:

1. जार्के-बेरा परीक्षण

• एक्सेल में जर्क-बेरा टेस्ट कैसे करें
• आर में जर्क-बेरा परीक्षण कैसे करें
• पायथन में जर्क-बेरा परीक्षण कैसे करें

2. शापिरो-विल्क परीक्षण

• आर में शापिरो-विल्क परीक्षण कैसे करें
• पायथन में शापिरो-विल्क परीक्षण कैसे करें

3. कोलमोगोरोव-स्मिरनोव परीक्षण

• आर में कोलमोगोरोव-स्मिरनोव परीक्षण कैसे करें
• पायथन में कोलमोगोरोव-स्मिरनोव परीक्षण कैसे करें

परिकल्पना 4: संबंधित जोड़े

पियर्सन सहसंबंध गुणांक यह भी मानता है कि डेटा सेट में प्रत्येक अवलोकन में मूल्यों की एक जोड़ी होनी चाहिए।

इस परिकल्पना को सत्यापित करना आसान है। उदाहरण के लिए, यदि आप वजन और ऊंचाई के बीच सहसंबंध की गणना कर रहे हैं, तो बस यह सत्यापित करें कि डेटासेट में प्रत्येक अवलोकन में वजन के लिए एक माप और ऊंचाई के लिए एक माप है।

परिकल्पना 5: कोई आउटलेयर नहीं

पियर्सन सहसंबंध गुणांक यह भी मानता है कि डेटा सेट में कोई चरम आउटलेर नहीं हैं, क्योंकि आउटलेर सहसंबंध गुणांक की गणना को दृढ़ता से प्रभावित करते हैं।

इसे स्पष्ट करने के लिए, निम्नलिखित डेटासेट पर विचार करें:

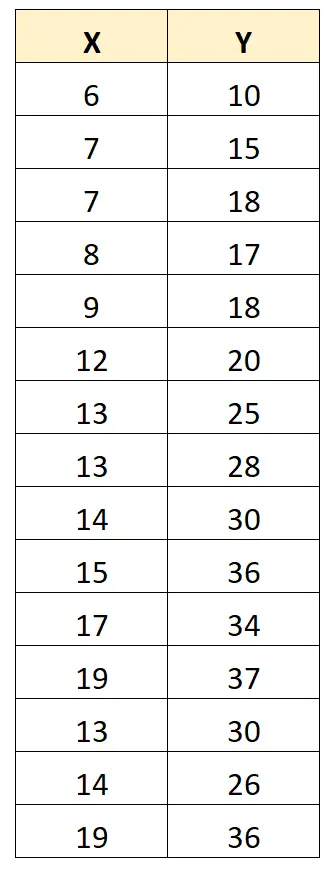
X और Y के बीच पियर्सन सहसंबंध गुणांक 0.949 है।

हालाँकि, मान लीजिए कि हमारे पास डेटासेट में एक बाहरी चीज़ है:

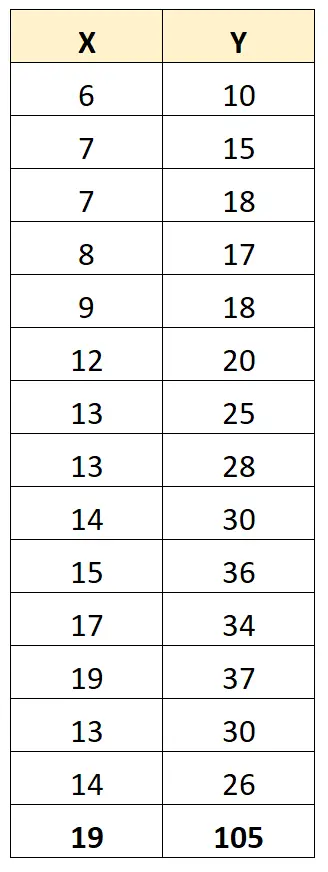
X और Y के बीच पियर्सन सहसंबंध गुणांक अब 0.711 है।

एक बाह्य दो चर के बीच पियर्सन सहसंबंध गुणांक को महत्वपूर्ण रूप से बदल देता है। इस मामले में, डेटासेट से आउटलेयर को हटाना समझदारी भरा हो सकता है।

संबंधित: संपूर्ण गाइड: डेटा में आउटलेर्स को कब हटाएं

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल पियर्सन सहसंबंध के बारे में अतिरिक्त जानकारी प्रदान करते हैं:

पियर्सन सहसंबंध गुणांक का परिचय
एपीए प्रारूप में पियर्सन सहसंबंध की रिपोर्ट कैसे करें
पियर्सन सहसंबंध गुणांक की मैन्युअल रूप से गणना कैसे करें