प्रभाव का आकार: यह क्या है और यह क्यों मायने रखता है
“परिणामों के बारे में सांख्यिकीय महत्व सबसे कम दिलचस्प बात है। आपको परिमाण माप के संदर्भ में परिणामों का वर्णन करने की आवश्यकता है – न केवल उपचार लोगों को प्रभावित करता है, बल्कि यह उन्हें कितना प्रभावित करता है। -जीन वी. ग्लास
आंकड़ों में, हम अक्सर यह निर्धारित करने के लिए पी-वैल्यू का उपयोग करते हैं कि दो समूहों के बीच सांख्यिकीय रूप से महत्वपूर्ण अंतर है या नहीं।
उदाहरण के लिए, मान लें कि हम जानना चाहते हैं कि क्या दो अलग-अलग अध्ययन तकनीकों से अलग-अलग परीक्षण स्कोर प्राप्त होते हैं। तो, हमारे पास 20 छात्रों का एक समूह है जो एक परीक्षण की तैयारी के लिए एक अध्ययन तकनीक का उपयोग कर रहा है जबकि 20 छात्रों का एक अन्य समूह एक अलग अध्ययन तकनीक का उपयोग कर रहा है। फिर हम प्रत्येक छात्र को एक ही परीक्षा देते हैं।
साधनों में अंतर निर्धारित करने के लिए दो-नमूना टी-परीक्षण चलाने के बाद, हम पाते हैं कि परीक्षण के लिए पी-मान 0.001 है। यदि हम 0.05 के महत्व स्तर का उपयोग करते हैं, तो इसका मतलब है कि दोनों समूहों के औसत परिणामों के बीच सांख्यिकीय रूप से महत्वपूर्ण अंतर है। इसलिए, अध्ययन तकनीक का परीक्षण परिणामों पर प्रभाव पड़ता है।
हालाँकि, जबकि पी-वैल्यू हमें बताता है कि अध्ययन तकनीक का परीक्षण स्कोर पर प्रभाव पड़ता है, यह हमें उस प्रभाव की भयावहता नहीं बताता है। इसे समझने के लिए, हमें प्रभाव का आकार जानना होगा।
प्रभाव का आकार क्या है?
प्रभाव आकार दो समूहों के बीच अंतर को मापने का एक तरीका है।
जबकि एक पी-वैल्यू हमें बता सकता है कि दो समूहों के बीच सांख्यिकीय रूप से महत्वपूर्ण अंतर है या नहीं, एक प्रभाव आकार हमें बता सकता है कि वह अंतर वास्तव में कितना बड़ा है। व्यवहार में, प्रभाव आकार पी-मानों की तुलना में जानने के लिए अधिक दिलचस्प और उपयोगी होते हैं।
आपके द्वारा किए जा रहे विश्लेषण के प्रकार के आधार पर, प्रभाव के आकार को मापने के तीन तरीके हैं:
1. मानकीकृत माध्य अंतर
जब आप दो समूहों के बीच माध्य अंतर का अध्ययन करना चाहते हैं, तो प्रभाव आकार की गणना करने का उचित तरीका मानकीकृत माध्य अंतर का उपयोग करना है। उपयोग करने के लिए सबसे लोकप्रिय सूत्र कोहेन के डी के रूप में जाना जाता है, जिसकी गणना निम्नानुसार की जाती है:
कोहेन का D = ( x1 – x2 )/ s
जहां x 1 और x 2 क्रमशः समूह 1 और समूह 2 के नमूना साधन हैं, और s उस जनसंख्या का मानक विचलन है जिससे दोनों समूह तैयार किए गए थे।
इस सूत्र का उपयोग करके, प्रभाव आकार की व्याख्या करना आसान है:
- 1 का d इंगित करता है कि दोनों समूहों के माध्य एक मानक विचलन से भिन्न हैं।
- 2 के ए डी का मतलब है कि समूह का मतलब दो मानक विचलन से भिन्न है।
- 2.5 का डी इंगित करता है कि दोनों माध्य 2.5 मानक विचलन से भिन्न हैं, इत्यादि।
प्रभाव आकार की व्याख्या करने का दूसरा तरीका यह है: 0.3 के प्रभाव आकार का मतलब है कि समूह 2 में औसत व्यक्ति का स्कोर समूह 1 के व्यक्ति के औसत से 0.3 मानक विचलन है और इसलिए समूह 1 के 62% के स्कोर से अधिक है। .
निम्न तालिका विभिन्न प्रभाव आकार और उनके संबंधित प्रतिशत दिखाती है:
| प्रभावी आकार | समूह 2 का प्रतिशत जो समूह 1 के लोगों के औसत से कम होगा |
|---|---|
| 0.0 | 50% |
| 0.2 | 58% |
| 0.4 | 66% |
| 0.6 | 73% |
| 0.8 | 79% |
| 1.0 | 84% |
| 1.2 | 88% |
| 1.4 | 92% |
| 1.6 | 95% |
| 1.8 | 96% |
| 2.0 | 98% |
| 2.5 | 99% |
| 3.0 | 99.9% |
प्रभाव का आकार जितना बड़ा होगा, प्रत्येक समूह में औसत व्यक्ति के बीच अंतर उतना ही अधिक होगा।
सामान्य तौर पर, 0.2 या उससे कम के डी को छोटा प्रभाव आकार माना जाता है, लगभग 0.5 के डी को मध्यम प्रभाव का आकार माना जाता है, और 0.8 या इससे बड़े के डी को बड़े प्रभाव का आकार माना जाता है।
इसलिए, यदि दो समूहों के माध्य कम से कम 0.2 मानक विचलन से भिन्न नहीं हैं, तो अंतर महत्वहीन है, भले ही पी-मान सांख्यिकीय रूप से महत्वपूर्ण हो।
2. सहसंबंध गुणांक
जब आप दो चर के बीच मात्रात्मक संबंध का अध्ययन करना चाहते हैं, तो प्रभाव आकार की गणना करने का सबसे आम तरीका पियर्सन सहसंबंध गुणांक का उपयोग करना है। यह दो चर X और Y के बीच रैखिक संबंध का एक माप है। इसका मान -1 और 1 के बीच है जहां:
- -1 दो चरों के बीच पूर्णतः नकारात्मक रैखिक सहसंबंध दर्शाता है
- 0 दो चरों के बीच कोई रैखिक सहसंबंध नहीं दर्शाता है
- 1 दो चरों के बीच पूर्णतः सकारात्मक रैखिक सहसंबंध दर्शाता है
पियर्सन सहसंबंध गुणांक की गणना करने का सूत्र काफी जटिल है, लेकिन रुचि रखने वालों के लिए इसे यहां पाया जा सकता है।
सहसंबंध गुणांक शून्य से जितना अधिक होगा, दो चरों के बीच रैखिक संबंध उतना ही मजबूत होगा। इसे वेरिएबल X और Y के मानों का एक सरल स्कैटरप्लॉट बनाकर भी देखा जा सकता है।
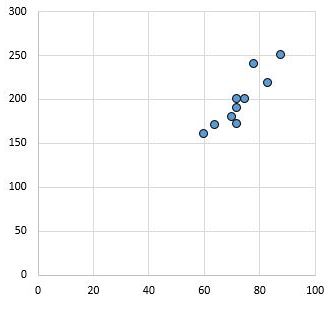
उदाहरण के लिए, निम्नलिखित स्कैटरप्लॉट r = 0.94 के सहसंबंध गुणांक के साथ दो चर के मान दिखाता है।
यह मान शून्य से बहुत दूर है, जो दर्शाता है कि दोनों चरों के बीच एक मजबूत सकारात्मक संबंध है।
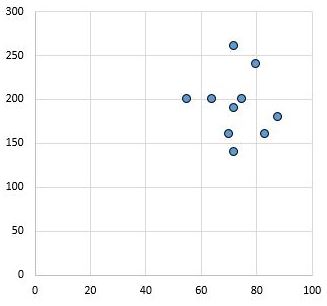
इसके विपरीत, निम्नलिखित स्कैटरप्लॉट दो चर के मान दिखाता है जिनका सहसंबंध गुणांक r = 0.03 है। यह मान शून्य के करीब है, जो दर्शाता है कि दोनों चरों के बीच वस्तुतः कोई संबंध नहीं है।
सामान्य तौर पर, यदि पियर्सन सहसंबंध गुणांक r का मान लगभग 0.1 है, तो प्रभाव का आकार छोटा माना जाता है, यदि r लगभग 0.3 है, तो मध्यम और यदि r 0.5 के बराबर या उससे अधिक है, तो प्रभाव का आकार बड़ा माना जाता है।
3. विषम अनुपात
जब आप किसी उपचार समूह में सफलता की संभावना बनाम नियंत्रण समूह में सफलता की संभावना का अध्ययन करना चाहते हैं, तो प्रभाव आकार की गणना करने का सबसे आम तरीका संभावना अनुपात का उपयोग करना है।
उदाहरण के लिए, मान लें कि हमारे पास निम्नलिखित तालिका है:
| प्रभावी आकार | #सफलता | #शतरंज |
|---|---|---|
| उपचार समूह | है | बी |
| नियंत्रण समूह | बनाम | डी |
अंतर अनुपात की गणना इस प्रकार की जाएगी:
विषम अनुपात = (AD) / (BC)
विषम अनुपात 1 से जितना अधिक होगा, उपचार के वास्तविक प्रभाव उत्पन्न करने की संभावना उतनी ही अधिक होगी।
पी-मानों पर प्रभाव आकारों का उपयोग करने के लाभ
पी-वैल्यू की तुलना में प्रभाव आकार के कई फायदे हैं:
1. प्रभाव का आकार हमें यह बेहतर अंदाज़ा लगाने में मदद करता है कि दो समूहों के बीच अंतर कितना बड़ा है या दो समूहों के बीच जुड़ाव कितना मजबूत है। पी-वैल्यू हमें केवल यह बता सकता है कि कोई महत्वपूर्ण अंतर या कोई महत्वपूर्ण जुड़ाव है या नहीं।
2. पी-वैल्यू के विपरीत, प्रभाव आकार का उपयोग विभिन्न सेटिंग्स में किए गए विभिन्न अध्ययनों के परिणामों की मात्रात्मक तुलना करने के लिए किया जा सकता है। इस कारण से, प्रभाव आकार का उपयोग अक्सर मेटा-विश्लेषण में किया जाता है।
3. P मान बड़े नमूना आकारों से प्रभावित हो सकते हैं। नमूना आकार जितना बड़ा होगा, परिकल्पना परीक्षण की सांख्यिकीय शक्ति उतनी ही अधिक होगी, जिससे वह छोटे प्रभावों का भी पता लगा सकेगा। इससे कम पी-वैल्यू हो सकता है, छोटे प्रभाव आकार के बावजूद जिसका कोई व्यावहारिक महत्व नहीं हो सकता है।
एक सरल उदाहरण इसे स्पष्ट रूप से समझा सकता है: मान लीजिए कि हम जानना चाहते हैं कि क्या दो अध्ययन तकनीकों से अलग-अलग परीक्षण स्कोर प्राप्त होते हैं। हमारे पास 20 छात्रों का एक समूह है जो एक अध्ययन तकनीक का उपयोग कर रहा है जबकि 20 छात्रों का एक अन्य समूह एक अलग अध्ययन तकनीक का उपयोग कर रहा है। फिर हम प्रत्येक छात्र को एक ही परीक्षा देते हैं।
समूह 1 का औसत स्कोर 90.65 है और समूह 2 का औसत स्कोर 90.75 है। नमूना 1 के लिए मानक विचलन 2.77 है और नमूना 2 के लिए मानक विचलन 2.78 है।
जब हम एक स्वतंत्र दो-नमूना टी-परीक्षण करते हैं, तो यह पता चलता है कि परीक्षण आँकड़ा -0.113 है और संबंधित पी-मान 0.91 है। औसत परीक्षण स्कोर के बीच का अंतर सांख्यिकीय रूप से महत्वपूर्ण नहीं है।
हालाँकि, विचार करें कि क्या दोनों नमूनों का नमूना आकार 200 था, लेकिन साधन और मानक विचलन बिल्कुल समान रहे।
इस मामले में, एक स्वतंत्र दो-नमूना टी-परीक्षण से पता चलेगा कि परीक्षण आँकड़ा -1.97 है और संबंधित पी-मान 0.05 से ठीक नीचे है। औसत परीक्षण स्कोर के बीच का अंतर सांख्यिकीय रूप से महत्वपूर्ण है।
बड़े नमूना आकारों के कारण सांख्यिकीय रूप से महत्वपूर्ण निष्कर्ष क्यों निकल सकते हैं इसका अंतर्निहित कारण टी -परीक्षण आंकड़ों की गणना के लिए उपयोग किया जाने वाला सूत्र है:
परीक्षण आँकड़ा t = [( x 1 – x 2 ) – d ] / (√ s 2 1 / n 1 + s 2 2 / n 2 )
ध्यान दें कि जब n 1 और n 2 छोटे होते हैं, तो t- परीक्षण आँकड़े का पूर्णांक हर छोटा होता है। और जब आप एक छोटी संख्या से भाग देते हैं, तो आपको एक बड़ी संख्या प्राप्त होती है। इसका मतलब यह है कि टी- परीक्षण आँकड़ा बड़ा होगा और संबंधित पी-मूल्य छोटा होगा, इस प्रकार सांख्यिकीय रूप से महत्वपूर्ण परिणाम प्राप्त होंगे।
एक अच्छा प्रभाव आकार क्या माना जाता है?
एक प्रश्न जो छात्र अक्सर पूछते हैं वह है: एक अच्छा प्रभाव आकार क्या माना जाता है?
संक्षिप्त उत्तर: एक प्रभाव का आकार “अच्छा” या “बुरा” नहीं हो सकता क्योंकि यह केवल दो समूहों के बीच अंतर के आकार या दो समूहों के बीच सहयोग की ताकत को मापता है।
हालाँकि, हम यह मापने के लिए निम्नलिखित नियमों का उपयोग कर सकते हैं कि किसी प्रभाव का परिमाण छोटा, मध्यम या बड़ा है:
कोहेन का डी:
- 0.2 या उससे कम के डी को छोटा प्रभाव आकार माना जाता है।
- 0.5 के डी को मध्यम प्रभाव आकार माना जाता है।
- 0.8 या इससे अधिक के डी को बड़े प्रभाव का आकार माना जाता है।
पियर्सन सहसंबंध गुणांक
- 0.1 के आसपास r का निरपेक्ष मान एक छोटा प्रभाव आकार माना जाता है।
- 0.3 के आसपास r का निरपेक्ष मान मध्यम प्रभाव आकार माना जाता है।
- 0.5 से अधिक r का निरपेक्ष मान एक बड़ा प्रभाव आकार माना जाता है।
हालाँकि, “मजबूत” सहसंबंध की परिभाषा एक क्षेत्र से दूसरे क्षेत्र में भिन्न हो सकती है। विभिन्न उद्योगों के बीच एक मजबूत सहसंबंध क्या माना जाता है, इसे बेहतर ढंग से समझने के लिए इस लेख का संदर्भ लें।