बहुपद वितरण

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 4, 2023 संभावना शून्य टिप्पणियां

यह आलेख बताता है कि सांख्यिकी में बहुपद वितरण क्या है। तो, आप पाएंगे कि बहुपद वितरण की परिभाषा क्या है, इसका सूत्र क्या है, एक हल किया गया अभ्यास और इस प्रकार के संभाव्यता वितरण के गुण क्या हैं। इसके अतिरिक्त, आप एक ऑनलाइन कैलकुलेटर से बहुपद वितरण की संभावना की गणना करने में सक्षम होंगे।

बहुपद वितरण क्या है?

बहुपद वितरण (या बहुपद वितरण ) एक संभाव्यता वितरण है जो कई परीक्षणों के बाद एक निश्चित संख्या में घटित होने वाली कई परस्पर अनन्य घटनाओं की संभावना का वर्णन करता है।

अर्थात्, यदि एक यादृच्छिक प्रयोग के परिणामस्वरूप तीन या अधिक विशिष्ट घटनाएँ हो सकती हैं और प्रत्येक घटना के अलग-अलग घटित होने की संभावना ज्ञात है, तो बहुपद वितरण का उपयोग इस संभावना की गणना करने के लिए किया जाता है कि जब कई प्रयोग किए जाते हैं, तो एक निश्चित संख्या में घटनाएँ घटित होती हैं। हर बार समय.

इसलिए बहुपद वितरण द्विपद वितरण का एक सामान्यीकरण है।

बहुपद वितरण सूत्र

बहुपद वितरण संभाव्यता की गणना करने के लिए, आपको पहले डेटा की कुल संख्या के फैक्टोरियल और प्रत्येक घटना की घटनाओं की संख्या के फैक्टोरियल के बीच भागफल निर्धारित करना होगा, और परिणाम को प्रत्येक घटना की संभावना के उत्पाद से गुणा करना होगा। उक्त घटना की घटनाओं की संख्या में लाया गया।

दूसरे शब्दों में, बहुपद वितरण का सूत्र इस प्रकार है:

सोना:

$P$

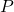
परिकलित बहुपद वितरण की प्रायिकता है।
$n$

किए गए परीक्षणों की कुल संख्या है.
$x_i$

घटना घटित होने की संख्या है

$i$

.
$p_i$

घटना घटित होने की प्रायिकता है

$i$

.

👉 आप बहुपद वितरण का अनुसरण करने वाले एक चर की संभावना की गणना करने के लिए नीचे दिए गए कैलकुलेटर का उपयोग कर सकते हैं।

बहुपद वितरण उदाहरण

बहुपद वितरण की अवधारणा को समझने के लिए, नीचे आपने बहुपद वितरण की संभावना की गणना का एक उदाहरण हल किया है।

एक स्टोर तीन अलग-अलग उत्पाद बेचता है। जब कोई ग्राहक खरीदारी करता है, तो संभावना है कि यह उत्पाद ए, उत्पाद बी या उत्पाद सी होगा क्रमशः 30%, 15% और 55% है। प्रायिकता ज्ञात कीजिए कि जब स्टोर ने 8 इकाइयाँ बेचीं, तो 2 उत्पाद A की, 1 उत्पाद B की, और 5 उत्पाद C की हैं।

परिभाषित समस्या एक बहुपद वितरण द्वारा नियंत्रित होती है, इसलिए इस प्रकार के संभाव्यता वितरण के लिए सूत्र लागू करना आवश्यक है:

$P=\cfrac{n!}{x_1!\cdot x_2!\cdot x_3!}\cdot p_1^{x_1}\cdot p_2^{x_2}\cdot p_3^{x_3}$

इसलिए हम समस्या से डेटा को सूत्र में प्रतिस्थापित करते हैं और संभाव्यता गणना करते हैं:

$P=\cfrac{8!}{2!\cdot 1!\cdot 5!}\cdot 0,30^{2}\cdot 0,15^{1}\cdot 0,55^{5}=0,114$

तो संभावना यह है कि समस्या कथन जो कहता है वह 11.4% है।

बहुपद वितरण कैलकुलेटर

पहले बॉक्स में प्रत्येक घटना के घटित होने की संख्या लिखें और उसी क्रम में दूसरे बॉक्स में प्रत्येक घटना के घटित होने की प्रायिकता लिखें। फिर अंतिम रिक्त स्थान में किए गए प्रयासों की कुल संख्या दर्ज करें।

डेटा को एक स्थान से अलग किया जाना चाहिए और दशमलव विभाजक के रूप में अवधि का उपयोग करके दर्ज किया जाना चाहिए।

बहुपद वितरण के गुण

बहुपद वितरण में निम्नलिखित विशेषताएं हैं:

एक बहुपद वितरण में, n परीक्षण चलाने पर घटना i घटित होने की संख्या का अपेक्षित मूल्य, घटना घटित होने की संभावना से गुणा किए गए परीक्षणों की कुल संख्या के बराबर होता है।

$E[x_i]=n\cdot p_i$

एक बहुपद वितरण में, घटना i के विचरण की गणना निम्नलिखित अभिव्यक्ति का उपयोग करके की जाती है:

$Var(x_i)=n\cdot p_i\cdot (1-p_i)$

इसी प्रकार, दो घटनाओं के बीच सहप्रसरण प्रत्येक घटना की संभावना को -1 से गुणा करने पर परीक्षणों की कुल संख्या के गुणनफल के बराबर होता है:

$Cov(x_i,x_j)=-n\cdot p_i\cdot p_j\qquad i\neq j$

बहुपद वितरण के लिए क्षण उत्पन्न करने वाला कार्य है:

$\displaystyle \left(\sum_{i=1}^k p_ie^{t_i}\right) ^n$

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने