दोहराए गए मापों की तीन धारणाएँ एनोवा

दोहराए गए माप एनोवा का उपयोग यह निर्धारित करने के लिए किया जाता है कि तीन या अधिक समूहों के साधनों के बीच सांख्यिकीय रूप से महत्वपूर्ण अंतर है या नहीं, जिनमें प्रत्येक समूह में समान विषय दिखाई देते हैं।

हालाँकि, बार-बार एनोवा उपाय करने से पहले, हमें यह सुनिश्चित करना होगा कि निम्नलिखित धारणाएँ पूरी हों:

1. स्वतंत्रता: प्रत्येक अवलोकन स्वतंत्र होना चाहिए।

2. सामान्यता: प्रतिक्रिया चर का वितरण सामान्य रूप से वितरित किया जाता है।

3. गोलाकारता: संबंधित समूहों के सभी संयोजनों के बीच अंतर का अंतर बराबर होना चाहिए।

यदि इनमें से एक या अधिक धारणाओं का उल्लंघन किया जाता है, तो एनोवा द्वारा दोहराए गए उपायों के परिणाम अविश्वसनीय हो सकते हैं।

इस लेख में, हम प्रत्येक धारणा के लिए एक स्पष्टीकरण प्रदान करते हैं, यह कैसे निर्धारित करें कि धारणा पूरी हो गई है या नहीं, और यदि यह पूरी नहीं होती है तो क्या करें।

परिकल्पना 1: स्वतंत्रता

दोहराया गया एनोवा माप यह मानता है कि आपके डेटा सेट में प्रत्येक अवलोकन अन्य सभी अवलोकनों से स्वतंत्र है।

यह कैसे निर्धारित किया जाए कि यह धारणा पूरी हुई है या नहीं

इस धारणा को सत्यापित करने का सबसे सरल तरीका यह सत्यापित करना है कि डेटासेट में प्रत्येक व्यक्ति को यादृच्छिक नमूना पद्धति का उपयोग करके जनसंख्या से यादृच्छिक रूप से नमूना लिया गया था।

यदि यादृच्छिक नमूनाकरण विधि का उपयोग किया गया था, तो प्रत्येक अवलोकन को स्वतंत्र माना जा सकता है।

यदि इस धारणा का सम्मान न किया जाए तो क्या करें?

यदि यह धारणा पूरी नहीं होती है, तो यह एक गंभीर समस्या है क्योंकि प्रत्येक व्यक्ति के मूल्य किसी न किसी तरह से एक-दूसरे से संबंधित हो सकते हैं।

अक्सर इस परिदृश्य में एकमात्र उपाय यादृच्छिक नमूना पद्धति का उपयोग करके नए अध्ययन के लिए व्यक्तियों को भर्ती करना है।

परिकल्पना 2: सामान्यता

दोहराया गया एनोवा माप मानता है कि प्रतिक्रिया चर का वितरण सामान्य रूप से वितरित किया जाता है।

यह कैसे निर्धारित किया जाए कि यह धारणा पूरी हुई है या नहीं

यह जांचने के दो तरीके हैं कि यह परिकल्पना सत्य है या नहीं:

1. एक हिस्टोग्राम या QQ प्लॉट बनाएं

आप हिस्टोग्राम या QQ प्लॉट बनाकर यह देख सकते हैं कि प्रतिक्रिया चर का वितरण लगभग सामान्य रूप से वितरित है या नहीं।

यदि आप एक हिस्टोग्राम बनाते हैं, तो बस जांच लें कि प्रतिक्रिया चर का वितरण लगभग “घंटी” आकार का अनुसरण करता है। यदि ऐसा है, तो आप अक्सर यह मान सकते हैं कि सामान्यता की धारणा पूरी हो गई है:

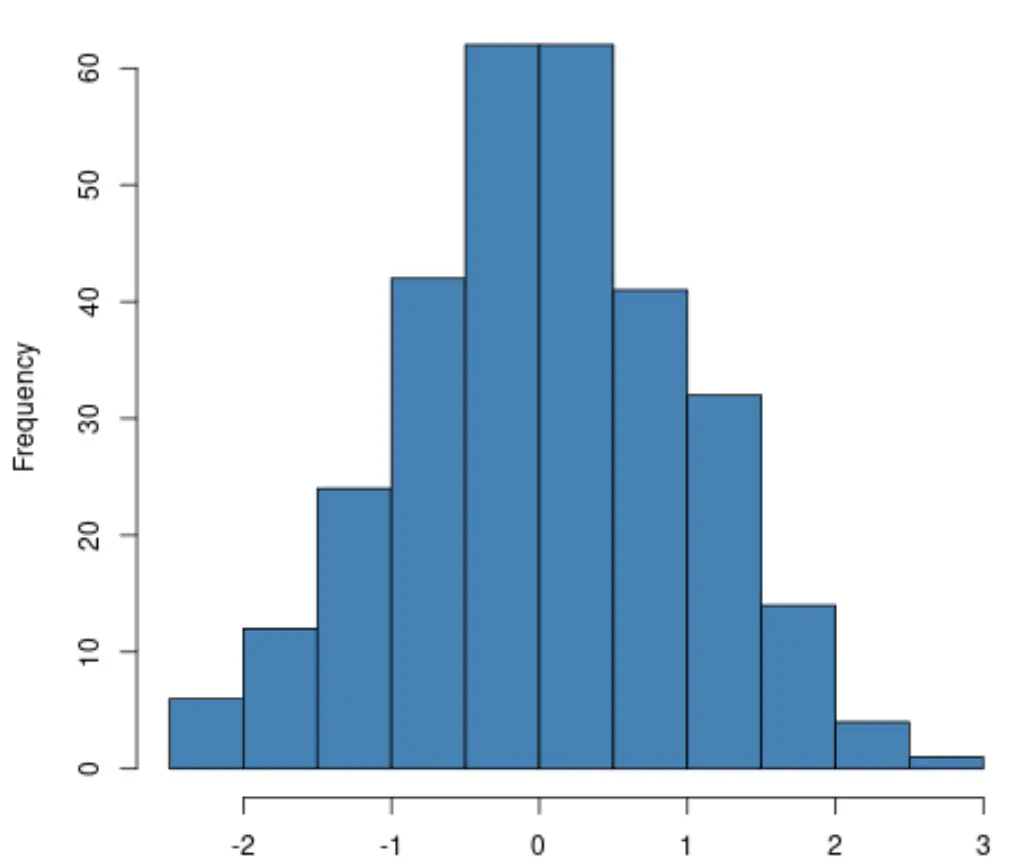
यदि आप QQ प्लॉट बना रहे हैं, तो यह देखने के लिए जांचें कि डेटा बिंदु एक सीधी विकर्ण रेखा के साथ स्थित हैं या नहीं। यदि ऐसा है, तो आप आम तौर पर मान सकते हैं कि सामान्यता की धारणा पूरी हो गई है:

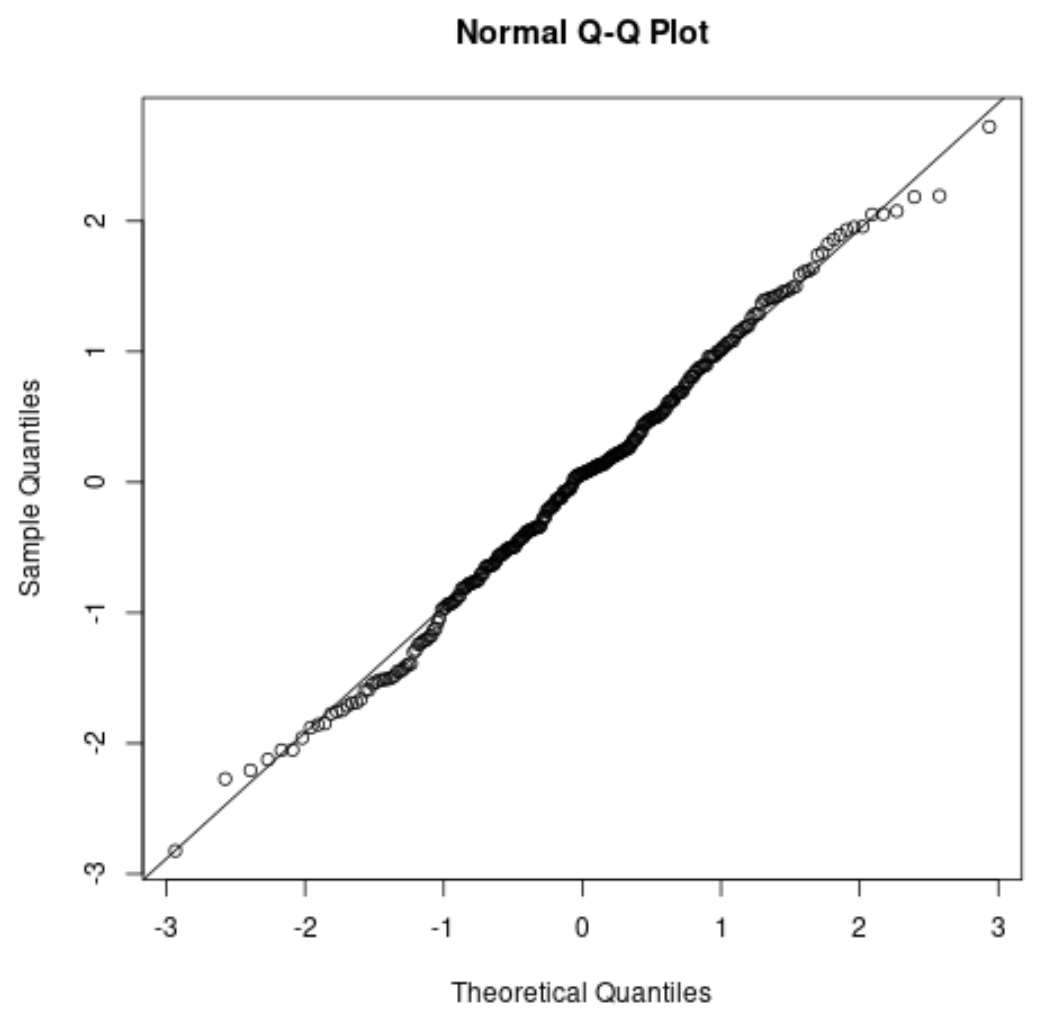
संबंधित: सामान्यता की जांच के लिए QQ प्लॉट्स का उपयोग कैसे करें

2. एक औपचारिक सांख्यिकीय परीक्षण करें

आप सामान्यता की जांच के लिए शापिरो-विल्क परीक्षण भी कर सकते हैं। यदि परीक्षण का पी-मान 0.05 से कम है, तो यह बताता है कि डेटा सामान्य रूप से वितरित नहीं है।

हालाँकि, सावधान रहें कि बहुत बड़े नमूनों के साथ काम करते समय, शापिरो-विल्क परीक्षण जैसे सांख्यिकीय परीक्षण लगभग हमेशा आपको बताएंगे कि आपका डेटा सामान्य नहीं है।

इस कारण से, हिस्टोग्राम और क्यूक्यू प्लॉट जैसे चार्ट का उपयोग करके अपने डेटा का दृश्य निरीक्षण करना अक्सर सबसे अच्छा होता है। केवल ग्राफ़ को देखकर आप बहुत अच्छा अंदाज़ा लगा सकते हैं कि डेटा सामान्य रूप से वितरित है या नहीं।

यदि इस धारणा का सम्मान न किया जाए तो क्या करें?

सामान्य तौर पर, बार-बार किए गए उपाय एनोवा को सामान्यता धारणा के उल्लंघन के खिलाफ काफी मजबूत माना जाता है, जब तक कि नमूना आकार काफी बड़ा हो।

यदि सामान्यता धारणा का गंभीर रूप से उल्लंघन किया गया है, तो आपके पास दो विकल्प हैं:

1. अपने डेटा के प्रतिक्रिया मूल्यों को बदलें ताकि वितरण अधिक सामान्य रूप से वितरित हो।

2. फ्राइडमैन परीक्षण जैसे समतुल्य गैर-पैरामीट्रिक परीक्षण करें जिसमें सामान्यता की धारणा की आवश्यकता नहीं होती है।

धारणा 3: गोलाकारता

दोहराया गया माप एनोवा गोलाकारता मानता है – यानी, संबंधित समूहों के सभी संयोजनों के बीच मतभेदों का अंतर बराबर होना चाहिए।

यदि यह धारणा पूरी नहीं होती है, तो एफ अनुपात बढ़ जाता है और एनोवा द्वारा दोहराए गए उपायों के परिणाम अविश्वसनीय हो जाते हैं।

यह कैसे निर्धारित किया जाए कि यह धारणा पूरी हुई है या नहीं

यह जांचने के लिए कि क्या यह धारणा पूरी हुई है, हम मौचली की गोलाकारता का परीक्षण कर सकते हैं।

यह परीक्षण निम्नलिखित शून्य और वैकल्पिक परिकल्पना का उपयोग करता है:

• एच ₀ : भिन्नता के प्रसरण बराबर होते हैं
• एच _ए : मतभेदों की भिन्नताएं समान नहीं हैं

यदि परीक्षण का पी-मान एक निश्चित स्तर के महत्व से नीचे है (उदाहरण के लिए α = 0.05), तो हम शून्य परिकल्पना को अस्वीकार करते हैं और निष्कर्ष निकालते हैं कि मतभेदों की भिन्नताएं समान नहीं हैं।

अन्यथा, यदि पी-मान एक निश्चित स्तर के महत्व से कम नहीं है (जैसे α = 0.05), तो हम शून्य परिकल्पना को अस्वीकार करने में विफल रहते हैं और निष्कर्ष निकालते हैं कि गोलाकारता की धारणा पूरी हो गई है।

आपके द्वारा उपयोग किए जाने वाले सांख्यिकीय सॉफ़्टवेयर के आधार पर, इस परीक्षण के परिणाम इस तरह दिखेंगे:

चूँकि पी-वैल्यू 0.05 से कम नहीं है, हम शून्य परिकल्पना को अस्वीकार करने में विफल रहेंगे और निष्कर्ष निकालेंगे कि गोलाकारता की धारणा इस विशेष उदाहरण में पूरी होती है।

यदि इस धारणा का सम्मान न किया जाए तो क्या करें?

यदि हम मौचली के गोलाकारता परीक्षण की शून्य परिकल्पना को अस्वीकार करते हैं, तो हम आम तौर पर दोहराए गए माप एनोवा तालिका में एफ मान की गणना करने के लिए उपयोग की जाने वाली स्वतंत्रता की डिग्री में सुधार लागू करते हैं।

ऐसे तीन सुधार हैं जिन्हें हम लागू कर सकते हैं:

• हुइन्ह-फेल्ट (कम से कम रूढ़िवादी)
• सेरे-गीसर
• निचली सीमा (सबसे अधिक रूढ़िवादी)

इनमें से प्रत्येक सुधार इस तथ्य को ध्यान में रखते हुए दोहराए गए माप एनोवा आउटपुट तालिका में पी-मान को बढ़ाता है कि गोलाकारता की धारणा का उल्लंघन होता है।

फिर हम इन पी-वैल्यू का उपयोग यह निर्धारित करने के लिए कर सकते हैं कि हमें एनोवा द्वारा दोहराए गए उपायों की शून्य परिकल्पना को अस्वीकार करना चाहिए या नहीं।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल एनोवा द्वारा दोहराए गए उपायों के बारे में अतिरिक्त जानकारी प्रदान करते हैं:

दोहराए गए उपायों का एक परिचय एनोवा
बार-बार माप एनोवा कैलकुलेटर
एनोवा द्वारा दोहराए गए उपायों के परिणामों की रिपोर्ट कैसे करें
एकतरफ़ा एनोवा और बार-बार मापे जाने वाले एनोवा: अंतर