बीटा वितरण
यह आलेख बताता है कि बीटा वितरण क्या है और इसका उपयोग किस लिए किया जाता है। इसी तरह, आप बीटा वितरण ग्राफ़ और इस प्रकार के संभाव्यता वितरण के गुणों को देख पाएंगे।
बीटा वितरण क्या है?
बीटा वितरण एक संभाव्यता वितरण है जिसे अंतराल (0,1) पर परिभाषित किया गया है और दो सकारात्मक मापदंडों द्वारा मानकीकृत किया गया है: α और β। दूसरे शब्दों में, बीटा वितरण का मान पैरामीटर α और β पर निर्भर करता है।
इसलिए, बीटा वितरण की मुख्य विशेषता यह है कि इसके आकार को पैरामीटर α और β द्वारा नियंत्रित किया जा सकता है। इसके अतिरिक्त, बीटा वितरण का उपयोग यादृच्छिक चर को परिभाषित करने के लिए किया जाता है जिसका मान 0 और 1 के बीच होता है।
यह इंगित करने के लिए कई संकेत हैं कि एक सतत यादृच्छिक चर बीटा वितरण द्वारा नियंत्रित होता है, सबसे आम हैं:
![Rendered by QuickLaTeX.com \begin{array}{c}X\sim B(\alpha,\beta)\\[2ex]X\sim Beta(\alpha,\beta)\\[2ex]X\sim \beta_{\alpha,\beta}\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-ee1d0d8a1624a017b8ef9ce8a67c694e_l3.png)
आंकड़ों में, बीटा वितरण के बहुत विविध अनुप्रयोग हैं। उदाहरण के लिए, बीटा वितरण का उपयोग विभिन्न नमूनों में प्रतिशत में भिन्नता का अध्ययन करने के लिए किया जाता है। इसी प्रकार, परियोजना प्रबंधन में, बीटा वितरण का उपयोग पर्ट विश्लेषण करने के लिए किया जाता है।
बीटा वितरण प्लॉट
बीटा वितरण की परिभाषा को ध्यान में रखते हुए, बीटा वितरण के घनत्व फ़ंक्शन और संभाव्यता वितरण फ़ंक्शन को नीचे प्लॉट किया गया है।
नीचे आप देख सकते हैं कि बीटा वितरण का घनत्व फ़ंक्शन ग्राफ पैरामीटर α और β के आधार पर कैसे भिन्न होता है।
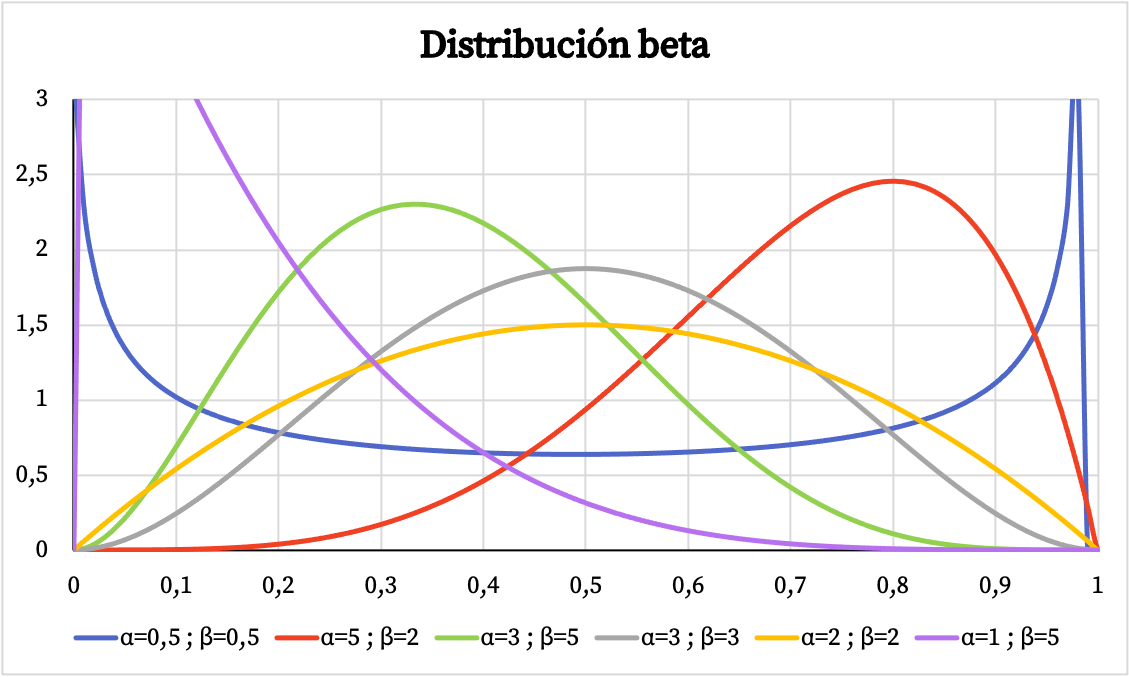
इसी प्रकार, नीचे आप पैरामीटर α और β के आधार पर बीटा वितरण की संचयी संभावना का ग्राफिकल प्रतिनिधित्व देख सकते हैं।
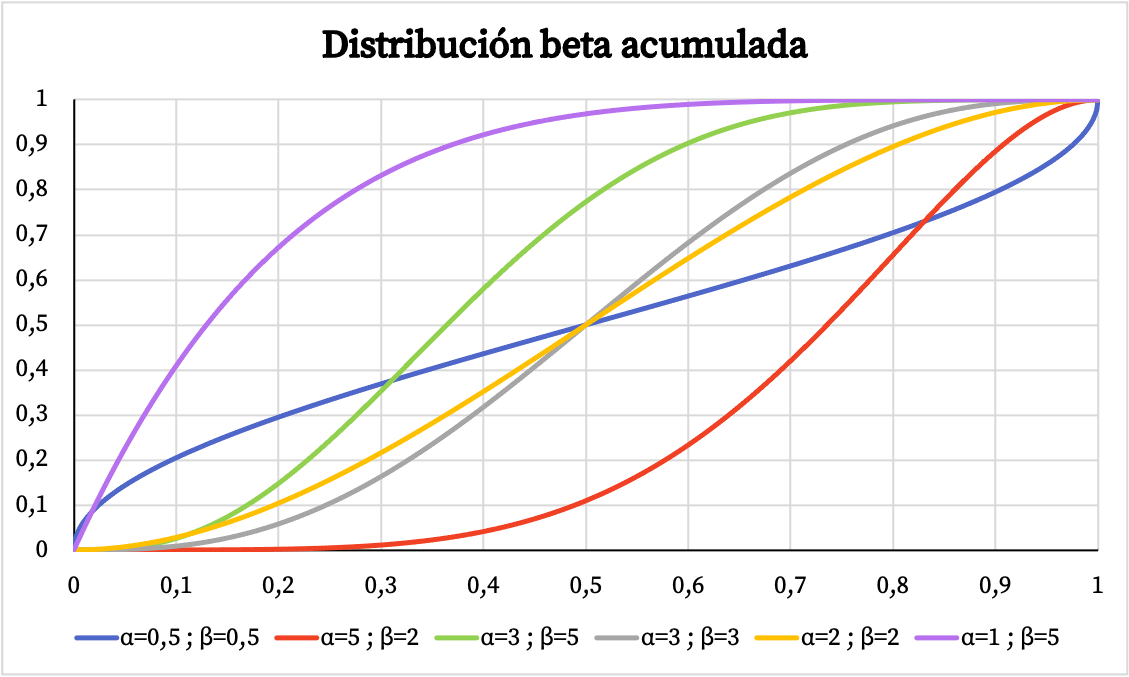
बीटा वितरण की विशेषताएँ
इस अनुभाग में हम देखेंगे कि बीटा वितरण की सबसे महत्वपूर्ण विशेषताएँ क्या हैं।
- बीटा वितरण के पैरामीटर α और β वास्तविक और सकारात्मक संख्याएं हैं।
![\begin{array}{c}\alpha >0\\[2ex] \beta >0\end{array}” title=”Rendered by QuickLaTeX.com” height=”54″ width=”44″ style=”vertical-align: 0px;”></p>
</p>
<ul>
<li> बीटा वितरण का डोमेन 0 से 1 तक है, दो चरम सीमाएँ शामिल नहीं हैं।</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-442bebaba847543d6db71cdf0127a4b0_l3.png)
![]()
- बीटा वितरण का माध्य अल्फा प्लस बीटा के योग से विभाजित अल्फा के बराबर है।
![Rendered by QuickLaTeX.com \begin{array}{c}X\sim B(\alpha,\beta)\\[2ex] E[X]=\cfrac{\alpha}{\alpha+\beta}\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-4530a8b72211111e8bec79b6388e00a7_l3.png)
- बीटा वितरण के विचरण की गणना निम्न सूत्र का उपयोग करके की जा सकती है:
![Rendered by QuickLaTeX.com \begin{array}{c}X\sim B(\alpha,\beta)\\[2ex] Var(X)=\cfrac{\alpha\cdot \beta}{(\alpha+\beta+1)\cdot (\alpha+\beta)^2}\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-71c6ef40db833722e63c56cd763d6601_l3.png)
- 1 से अधिक अल्फा और बीटा मानों के लिए, बीटा वितरण मोड को निम्नलिखित अभिव्यक्ति के साथ आसानी से पाया जा सकता है:
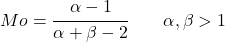
![]()
जहां B(α,β) बीटा फ़ंक्शन है, जिसे इस प्रकार परिभाषित किया गया है:
![]()
- बीटा वितरण का संचयी संभाव्यता फ़ंक्शन है:
![]()
जहां B(x;α,β) अधूरा बीटा फ़ंक्शन है, जिसे इस प्रकार परिभाषित किया गया है:
![]()
- यदि X एक बीटा वितरण द्वारा परिभाषित एक चर है, तो 1-X एक बीटा वितरण द्वारा परिभाषित एक चर है जिसके अल्फा और बीटा पैरामीटर क्रमशः मूल बीटा वितरण के बीटा और अल्फा पैरामीटर हैं।
![]()
- यदि बीटा वितरण के अल्फा और बीटा पैरामीटर दोनों 1 के बराबर हैं, तो वितरण पैरामीटर 0 और 1 के एक समान वितरण के बराबर है।
![]()