सांख्यिकी में बीटा स्तर क्या है? (परिभाषा & #038; उदाहरण)

आंकड़ों में, हम यह निर्धारित करने के लिए परिकल्पना परीक्षण का उपयोग करते हैं कि जनसंख्या पैरामीटर के बारे में एक परिकल्पना सत्य है या नहीं।

एक परिकल्पना परीक्षण में हमेशा निम्नलिखित दो परिकल्पनाएँ होती हैं:

शून्य परिकल्पना (एच ₀ ): नमूना डेटा जनसंख्या पैरामीटर के संबंध में प्रमुख धारणा के अनुरूप है।

वैकल्पिक परिकल्पना ( _एचए ): नमूना डेटा से पता चलता है कि शून्य परिकल्पना में बताई गई परिकल्पना सत्य नहीं है। दूसरे शब्दों में, एक गैर-यादृच्छिक कारण डेटा को प्रभावित करता है।

जब भी हम कोई परिकल्पना परीक्षण करते हैं, तो हमेशा चार संभावित परिणाम होते हैं:

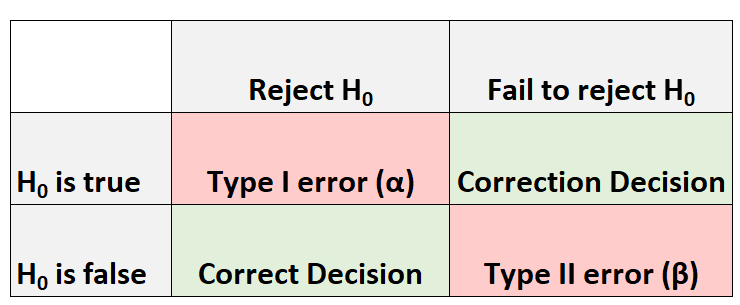
हम दो प्रकार की गलतियाँ कर सकते हैं:

• प्रकार I त्रुटि: हम शून्य परिकल्पना को अस्वीकार कर देते हैं जबकि यह वास्तव में सत्य है। इस प्रकार की त्रुटि होने की संभावना को α दर्शाया गया है।
• टाइप II त्रुटि: हम शून्य परिकल्पना को अस्वीकार करने में विफल रहते हैं जब यह वास्तव में गलत होती है। इस प्रकार की त्रुटि होने की संभावना β नोट की गई है।

अल्फा और बीटा के बीच संबंध

आदर्श रूप से, शोधकर्ता चाहते हैं कि टाइप I त्रुटि होने की संभावना और टाइप II त्रुटि होने की संभावना कम हो।

हालाँकि, इन दोनों संभावनाओं के बीच एक समझौता है। यदि हम अल्फा स्तर को कम करते हैं, तो हम एक अशक्त परिकल्पना को अस्वीकार करने की संभावना कम कर सकते हैं जब यह वास्तव में सच है, लेकिन यह वास्तव में बीटा स्तर को बढ़ाता है – संभावना है कि हम गलत होने पर अशक्त परिकल्पना को अस्वीकार करने में विफल रहते हैं।

शक्ति और बीटा के बीच संबंध

एक परिकल्पना परीक्षण की शक्ति किसी प्रभाव या अंतर का पता लगाने की संभावना को संदर्भित करती है जब कोई प्रभाव या अंतर वास्तव में मौजूद होता है। दूसरे शब्दों में, यह एक झूठी शून्य परिकल्पना को सही ढंग से खारिज करने की संभावना है।

इसकी गणना इस प्रकार की जाती है:

पावर = 1 – β

सामान्य तौर पर शोधकर्ता चाहते हैं कि किसी परीक्षण की शक्ति अधिक हो ताकि यदि कोई प्रभाव या अंतर हो तो परीक्षण उसका पता लगा सके।

उपरोक्त समीकरण से, हम देख सकते हैं कि किसी परीक्षण की शक्ति बढ़ाने का सबसे अच्छा तरीका बीटा स्तर को कम करना है। और बीटा स्तर को कम करने का सबसे अच्छा तरीका आमतौर पर नमूना आकार बढ़ाना है।

निम्नलिखित उदाहरण दिखाते हैं कि परिकल्पना परीक्षण के बीटा स्तर की गणना कैसे करें और प्रदर्शित करें कि नमूना आकार बढ़ाने से बीटा स्तर कम क्यों हो सकता है।

उदाहरण 1: परिकल्पना परीक्षण के लिए बीटा की गणना करें

मान लीजिए कि एक शोधकर्ता यह परीक्षण करना चाहता है कि किसी कारखाने में उत्पादित विजेट का औसत वजन 500 औंस से कम है या नहीं। हम जानते हैं कि वज़न का मानक विचलन 24 औंस है और शोधकर्ता 40 विजेट्स का एक यादृच्छिक नमूना एकत्र करने का निर्णय लेता है।

यह α = 0.05 पर निम्नलिखित परिकल्पना को साकार करेगा:

• एच ₀ : µ = 500
• एच _ए : μ <500

अब कल्पना करें कि उत्पादित विजेट का औसत वजन वास्तव में 490 औंस है। दूसरे शब्दों में, शून्य परिकल्पना को अस्वीकार कर दिया जाना चाहिए।

हम बीटा स्तर की गणना करने के लिए निम्नलिखित चरणों का उपयोग कर सकते हैं – शून्य परिकल्पना को अस्वीकार न करने की संभावना जबकि वास्तव में इसे अस्वीकार कर दिया जाना चाहिए:

चरण 1: नो-अस्वीकृति क्षेत्र खोजें।

क्रिटिकल Z मान कैलकुलेटर के अनुसार, α = 0.05 पर बायां क्रिटिकल मान -1.645 है।

चरण 2: वह न्यूनतम नमूना ढूंढें जिसे हम अस्वीकार करने में विफल रहेंगे।

परीक्षण आँकड़े की गणना z = ( x – μ) / (s/ √n ) के रूप में की जाती है

तो, हम नमूना माध्य के लिए इस समीकरण को हल कर सकते हैं:

• x = µ – z*(s/ √n )
• x = 500 – 1.645*(24/ √40 )
• एक्स = 493.758

चरण 3: संभावना निर्धारित करें कि न्यूनतम नमूना माध्य वास्तव में घटित होगा।

हम इस संभावना की गणना इस प्रकार कर सकते हैं:

• पी(जेड ≥ (493.758 – 490) / (24/√ 40 ))
• पी(जेड ≥ 0.99)

सामान्य CDF कैलकुलेटर के अनुसार, Z ≥ 0.99 होने की प्रायिकता 0.1611 है।

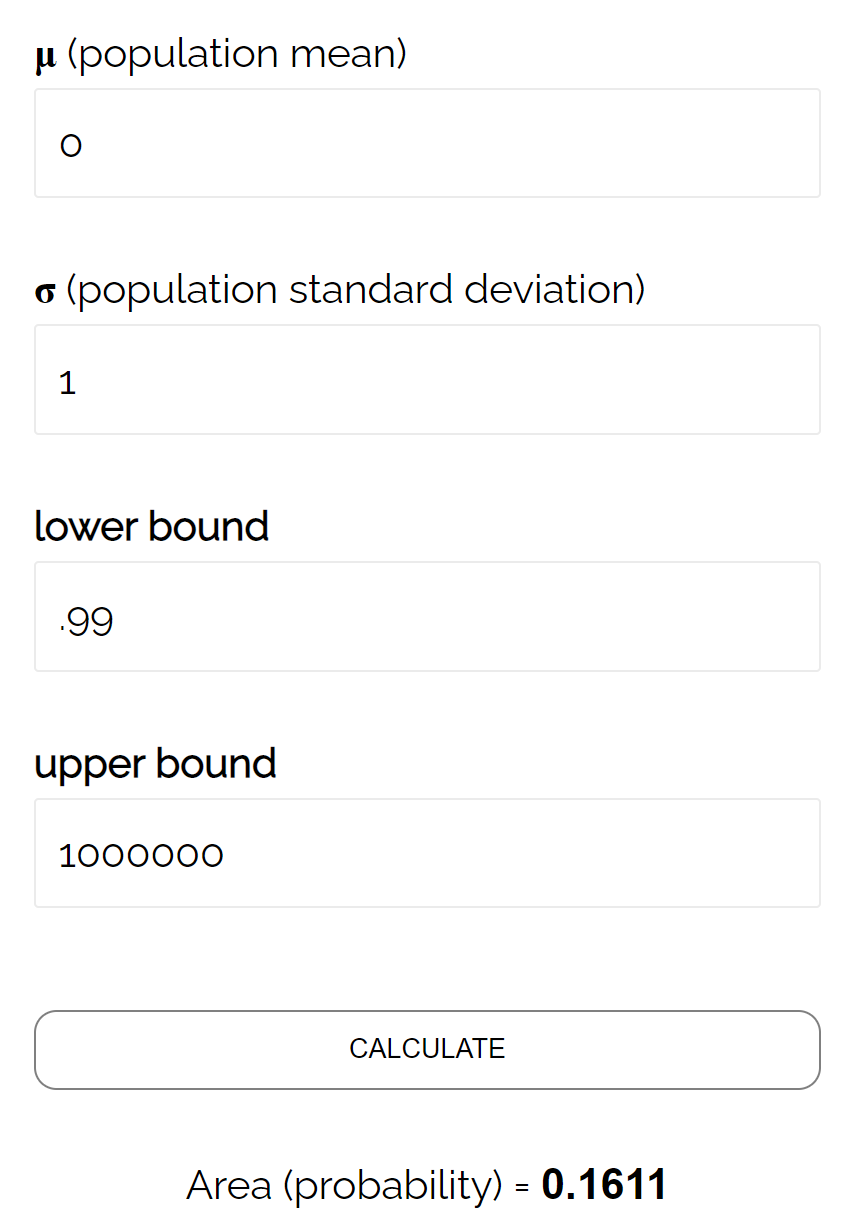
इस प्रकार, इस परीक्षण के लिए बीटा स्तर β = 0.1611 है। इसका मतलब यह है कि यदि वास्तविक औसत 490 औंस है तो अंतर का पता न लगने की 16.11% संभावना है।

उदाहरण 2: बड़े नमूना आकार वाले परीक्षण के लिए बीटा की गणना करें

अब मान लीजिए कि शोधकर्ता बिल्कुल वही परिकल्पना परीक्षण करता है, लेकिन इसके बजाय n = 100 विजेट के नमूने का उपयोग करता है। इस परीक्षण के लिए बीटा स्तर की गणना करने के लिए हम वही तीन चरण दोहरा सकते हैं:

चरण 1: नो-अस्वीकृति क्षेत्र खोजें।

क्रिटिकल Z मान कैलकुलेटर के अनुसार, α = 0.05 पर बायां क्रिटिकल मान -1.645 है।

चरण 2: वह न्यूनतम नमूना ढूंढें जिसे हम अस्वीकार करने में विफल रहेंगे।

परीक्षण आँकड़े की गणना z = ( x – μ) / (s/ √n ) के रूप में की जाती है

तो, हम नमूना माध्य के लिए इस समीकरण को हल कर सकते हैं:

• x = µ – z*(s/ √n )
• x = 500 – 1.645*(24/√ 100 )
• एक्स = 496.05

चरण 3: संभावना निर्धारित करें कि न्यूनतम नमूना माध्य वास्तव में घटित होगा।

हम इस संभावना की गणना इस प्रकार कर सकते हैं:

• पी(जेड ≥ (496.05 – 490) / (24/√ 100 ))
• पी(जेड ≥ 2.52)

सामान्य CDF कैलकुलेटर के अनुसार, Z ≥ 2.52 की प्रायिकता 0.0059 है।

इस प्रकार, इस परीक्षण के लिए बीटा स्तर β = 0.0059 है। इसका मतलब यह है कि यदि वास्तविक औसत 490 औंस है तो अंतर का पता न लगने की केवल 0.59% संभावना है।

ध्यान दें कि केवल नमूना आकार को 40 से बढ़ाकर 100 करके, शोधकर्ता बीटा स्तर को 0.1611 से घटाकर 0.0059 करने में सक्षम था।

बोनस: किसी परीक्षण के बीटा स्तर की स्वचालित रूप से गणना करने के लिए इस प्रकार II त्रुटि कैलकुलेटर का उपयोग करें।

अतिरिक्त संसाधन

परिकल्पना परीक्षण का परिचय
शून्य परिकल्पना कैसे लिखें (5 उदाहरण)
पी मूल्यों और सांख्यिकीय महत्व की व्याख्या