स्टाटा में प्रतिगमन में मजबूत मानक त्रुटियों का उपयोग कैसे करें

मल्टीपल लीनियर रिग्रेशन एक ऐसी विधि है जिसका उपयोग हम कई व्याख्यात्मक चर और एक प्रतिक्रिया चर के बीच संबंध को समझने के लिए कर सकते हैं।

दुर्भाग्य से, एक समस्या जो अक्सर प्रतिगमन में होती है उसे विषमलैंगिकता के रूप में जाना जाता है, जिसमें मापा मूल्यों की एक सीमा पर अवशेषों के विचरण में एक व्यवस्थित परिवर्तन होता है।

इससे प्रतिगमन गुणांक अनुमानों के विचरण में वृद्धि होती है, लेकिन प्रतिगमन मॉडल इसे ध्यान में नहीं रखता है। इससे यह अधिक संभावना हो जाती है कि एक प्रतिगमन मॉडल यह दावा करेगा कि मॉडल में एक शब्द सांख्यिकीय रूप से महत्वपूर्ण है, जबकि वास्तव में ऐसा नहीं है।

इस समस्या का समाधान करने का एक तरीका मजबूत मानक त्रुटियों का उपयोग करना है, जो विषमलैंगिकता की समस्या के लिए अधिक “मजबूत” हैं और प्रतिगमन गुणांक की वास्तविक मानक त्रुटि का अधिक सटीक माप प्रदान करते हैं।

यह ट्यूटोरियल बताता है कि स्टाटा में प्रतिगमन विश्लेषण में मजबूत मानक त्रुटियों का उपयोग कैसे करें।

उदाहरण: स्टाटा में मजबूत मानक त्रुटियाँ

हम प्रतिगमन में मजबूत मानक त्रुटियों का उपयोग करने के तरीके को स्पष्ट करने के लिए स्वचालित रूप से एकीकृत स्टेटा डेटासेट का उपयोग करेंगे।

चरण 1: डेटा लोड करें और प्रदर्शित करें।

सबसे पहले, डेटा लोड करने के लिए निम्न कमांड का उपयोग करें:

सिस्टम का स्वचालित उपयोग

फिर निम्नलिखित कमांड का उपयोग करके कच्चा डेटा प्रदर्शित करें:

बीआर

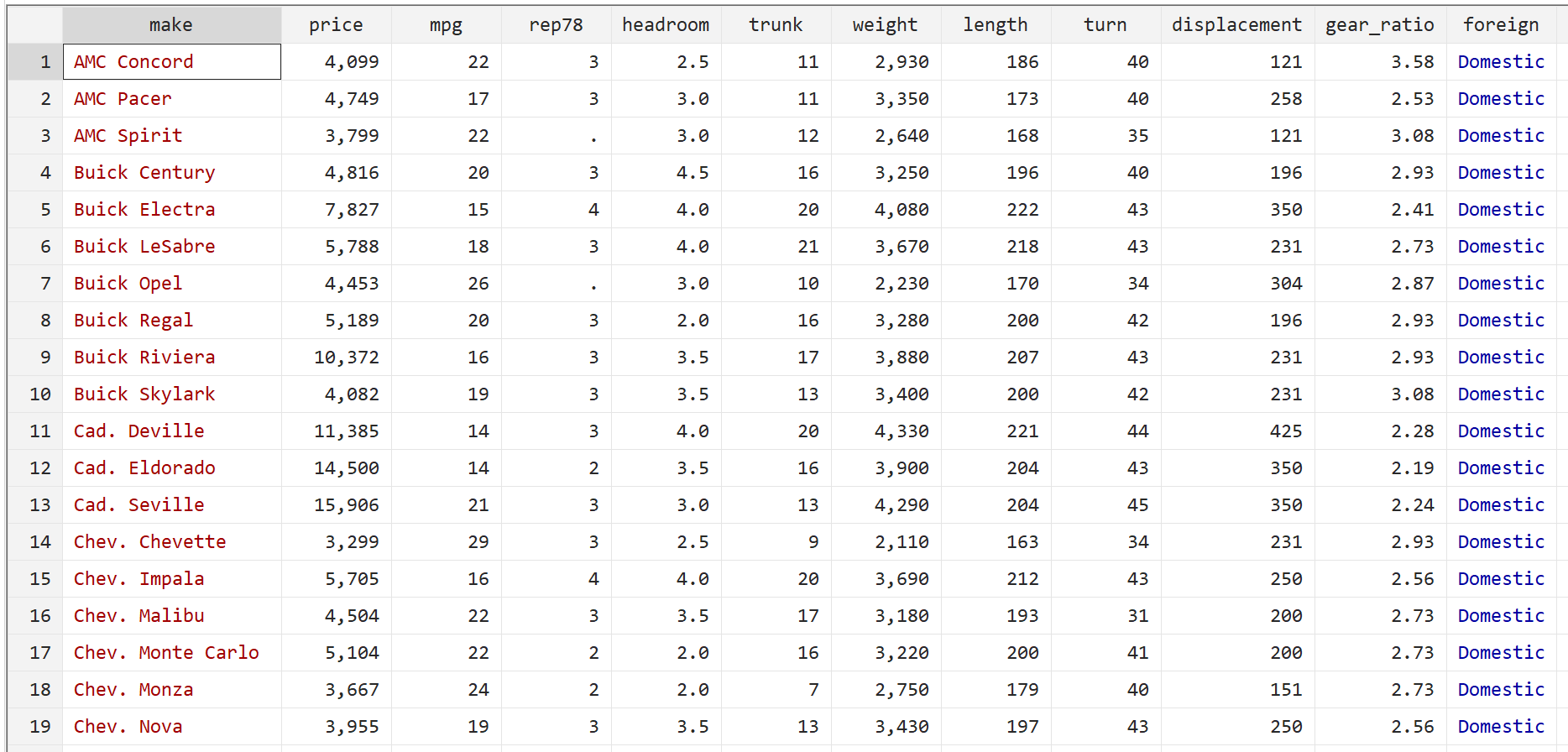
चरण 2: मजबूत मानक त्रुटियों के बिना एकाधिक रैखिक प्रतिगमन निष्पादित करें।

इसके बाद, हम प्रतिक्रिया चर के रूप में मूल्य और व्याख्यात्मक चर के रूप में एमपीजी और वजन का उपयोग करके एकाधिक रैखिक प्रतिगमन करने के लिए निम्नलिखित कमांड दर्ज करेंगे:

प्रतिगमन मूल्य एमपीजी वजन

चरण 3: मजबूत मानक त्रुटियों का उपयोग करके एकाधिक रैखिक प्रतिगमन करें।

अब हम बिल्कुल वही एकाधिक रैखिक प्रतिगमन निष्पादित करेंगे, लेकिन इस बार हम vce (मजबूत) कमांड का उपयोग करेंगे ताकि स्टाटा को पता चले कि मजबूत मानक त्रुटियों का उपयोग कैसे करें:

प्रतिगमन मूल्य एमपीजी वजन, वीसीई (मजबूत)

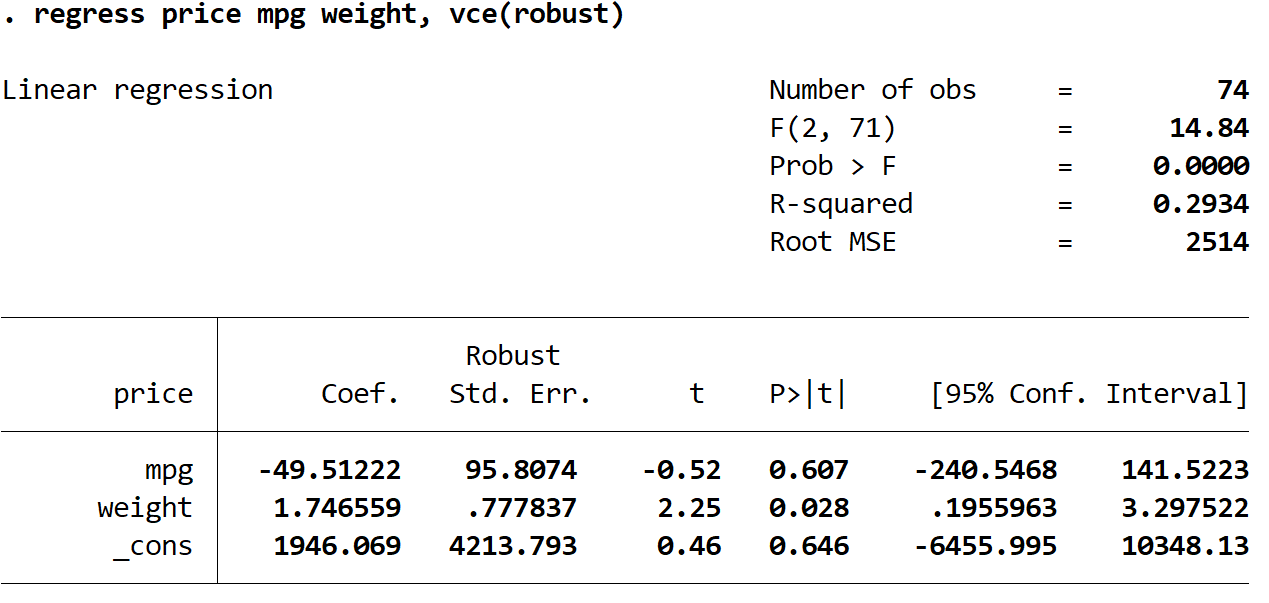
यहां ध्यान देने योग्य कुछ दिलचस्प बातें हैं:

1. गुणांक अनुमान वही रहे . जब हम मजबूत मानक त्रुटियों का उपयोग करते हैं, तो गुणांक अनुमान बिल्कुल नहीं बदलता है। ध्यान दें कि दोनों प्रतिगमनों के लिए mpg, भार और स्थिरांक के लिए गुणांक अनुमान इस प्रकार हैं:

• एमपीजी: -49.51222
• वज़न: 1.746559
• _विरुद्ध: 1946.069

2. मानक त्रुटियाँ बदल गई हैं । ध्यान दें कि जब हमने मजबूत मानक त्रुटियों का उपयोग किया, तो प्रत्येक गुणांक अनुमान के लिए मानक त्रुटियां बढ़ गईं।

नोट: ज्यादातर मामलों में, मजबूत मानक त्रुटियां सामान्य मानक त्रुटियों से बड़ी होंगी, लेकिन दुर्लभ मामलों में यह संभव है कि मजबूत मानक त्रुटियां वास्तव में छोटी होंगी।

3. प्रत्येक गुणांक का परीक्षण आँकड़ा बदल गया है। ध्यान दें कि प्रत्येक परीक्षण आँकड़े का निरपेक्ष मान , t , कम हो गया है। वास्तव में, परीक्षण आँकड़ों की गणना अनुमानित गुणांक को मानक त्रुटि से विभाजित करके की जाती है। इस प्रकार, मानक त्रुटि जितनी बड़ी होगी, परीक्षण आँकड़ों का निरपेक्ष मान उतना ही छोटा होगा।

4. पी-वैल्यू बदल गए हैं । ध्यान दें कि प्रत्येक वेरिएबल के लिए पी-वैल्यू में भी वृद्धि हुई है। ऐसा इसलिए है क्योंकि छोटे परीक्षण आँकड़े बड़े पी-मानों से जुड़े होते हैं।

यद्यपि हमारे गुणांकों के लिए पी मान बदल गए हैं, एमपीजी चर अभी भी α = 0.05 पर सांख्यिकीय रूप से महत्वपूर्ण नहीं है और चर वजन अभी भी α = 0.05 पर सांख्यिकीय रूप से महत्वपूर्ण है।