मानकीकृत अवशेष क्या हैं?

अवशिष्ट एक प्रतिगमन मॉडल में देखे गए मूल्य और अनुमानित मूल्य के बीच का अंतर है।

इसकी गणना इस प्रकार की जाती है:

अवशिष्ट = प्रेक्षित मूल्य – अनुमानित मूल्य

यदि हम देखे गए मानों को प्लॉट करते हैं और फिटेड रिग्रेशन लाइन को सुपरइम्पोज़ करते हैं, तो प्रत्येक अवलोकन के लिए अवशेष अवलोकन और रिग्रेशन लाइन के बीच ऊर्ध्वाधर दूरी होगी:

एक प्रकार का अवशिष्ट जिसे हम अक्सर प्रतिगमन मॉडल में आउटलेर्स की पहचान करने के लिए उपयोग करते हैं , मानकीकृत अवशिष्ट कहा जाता है।

इसकी गणना इस प्रकार की जाती है:

आर _आई = ई _आई / एस(ई _आई ) = ई _आई / आरएसई√ 1-एच _ii

सोना:

• e _i : i वां ^{अवशेष}
• आरएसई: मॉडल की अवशिष्ट मानक त्रुटि
• h _ii : ^ith अवलोकन का उदय

व्यवहार में, हम अक्सर किसी भी मानकीकृत अवशिष्ट पर विचार करते हैं जिसका पूर्ण मूल्य 3 से अधिक है।

इसका मतलब यह नहीं है कि हम इन टिप्पणियों को मॉडल से हटा देंगे, लेकिन हमें यह सत्यापित करने के लिए कम से कम उनका आगे अध्ययन करना चाहिए कि वे डेटा प्रविष्टि त्रुटि या किसी अन्य अजीब घटना का परिणाम नहीं हैं।

नोट: कभी-कभी मानकीकृत अवशेषों को “इन-हाउस अध्ययनित अवशेष” भी कहा जाता है।

उदाहरण: मानकीकृत अवशेषों की गणना कैसे करें

मान लीजिए कि हमारे पास कुल 12 अवलोकनों के साथ निम्नलिखित डेटासेट हैं:

यदि हम इस डेटा सेट में एक रेखीय प्रतिगमन रेखा को फिट करने के लिए सांख्यिकीय सॉफ़्टवेयर (जैसे आर , एक्सेल , पायथन , स्टेटा , आदि) का उपयोग करते हैं, तो हम पाएंगे कि सबसे अच्छी फिट की रेखा इस प्रकार है:

y = 29.63 + 0.7553x

इस पंक्ति का उपयोग करके, हम X के मान के आधार पर प्रत्येक Y मान के लिए अनुमानित मान की गणना कर सकते हैं। उदाहरण के लिए, पहले अवलोकन का अनुमानित मान होगा:

y = 29.63 + 0.7553*(8) = 35.67

फिर हम इस अवलोकन के लिए शेष की गणना इस प्रकार कर सकते हैं:

अवशिष्ट = प्रेक्षित मूल्य – अनुमानित मूल्य = 41 – 35.67 = 5.33

हम प्रत्येक अवलोकन के लिए अवशेष खोजने के लिए इस प्रक्रिया को दोहरा सकते हैं:

हम यह पता लगाने के लिए सांख्यिकीय सॉफ़्टवेयर का भी उपयोग कर सकते हैं कि मॉडल की अवशिष्ट मानक त्रुटि 4.44 है।

और, यद्यपि यह इस ट्यूटोरियल के दायरे से परे है, हम प्रत्येक अवलोकन के लिए उत्तोलन आँकड़ा (एच _ii ) खोजने के लिए सॉफ़्टवेयर का उपयोग कर सकते हैं:

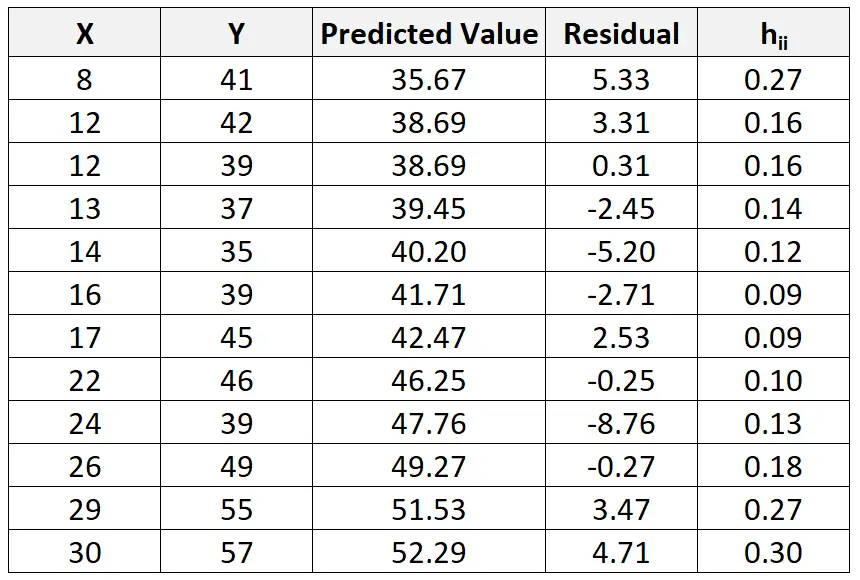
फिर हम प्रत्येक अवलोकन के लिए मानकीकृत अवशिष्ट की गणना करने के लिए निम्नलिखित सूत्र का उपयोग कर सकते हैं:

आर _आई = ई _आई / आरएसई√ 1-एच _ii

उदाहरण के लिए, पहले अवलोकन के लिए मानकीकृत अवशेष की गणना निम्नानुसार की जाती है:

आर _आई = 5.33 / 4.44√ 1-0.27 = 1.404

हम प्रत्येक अवलोकन के लिए मानकीकृत अवशेष खोजने के लिए इस प्रक्रिया को दोहरा सकते हैं:

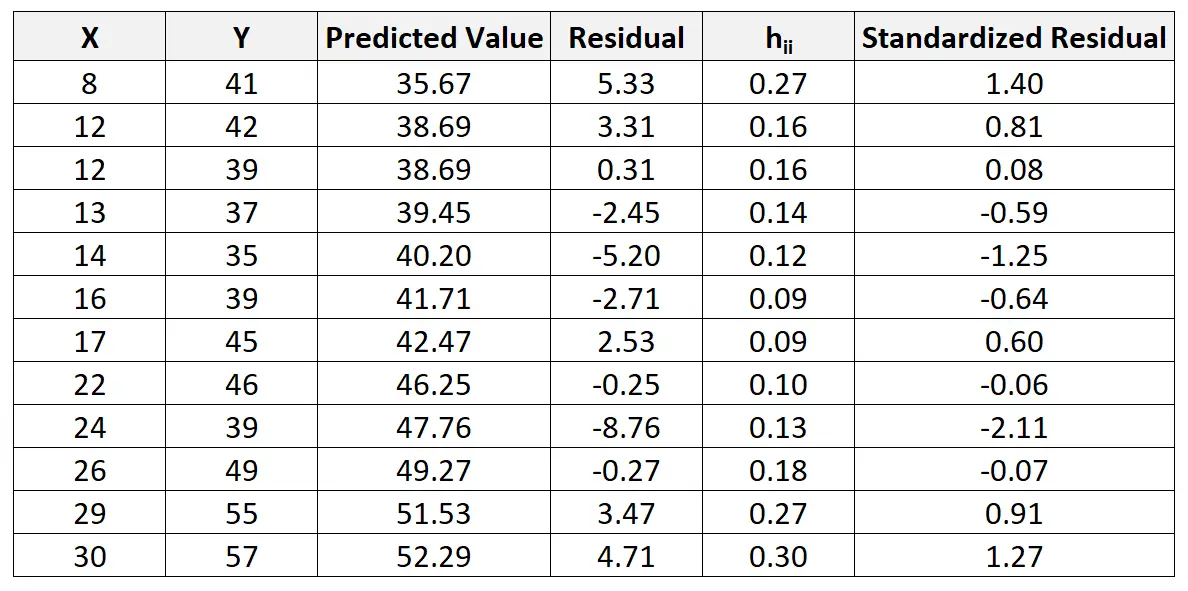
फिर हम यह देखने के लिए मानकीकृत अवशेषों के विरुद्ध पूर्वानुमानित मूल्यों का एक त्वरित स्कैटरप्लॉट बना सकते हैं कि क्या मानकीकृत अवशेषों में से कोई भी 3 की पूर्ण मूल्य सीमा से अधिक है:

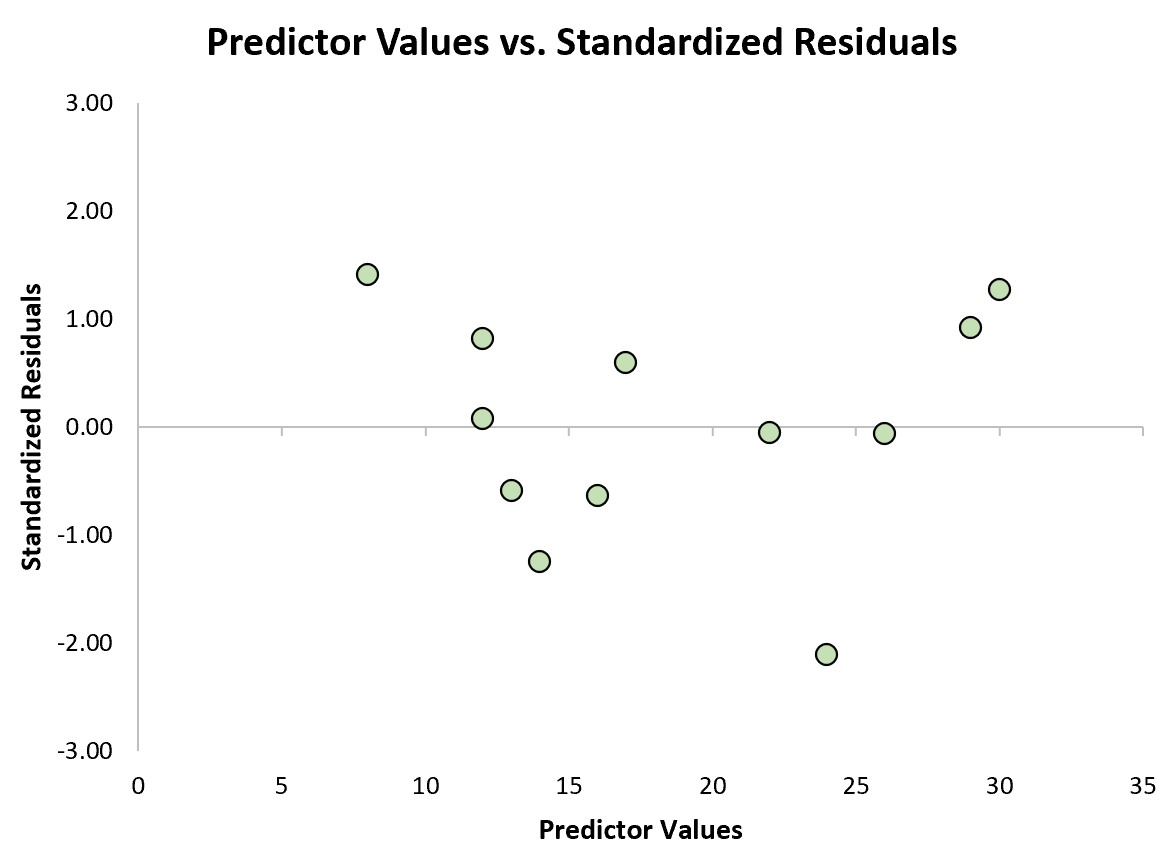
ग्राफ़ से, हम देख सकते हैं कि कोई भी मानकीकृत अवशेष 3 के निरपेक्ष मान से अधिक नहीं है। इस प्रकार, कोई भी अवलोकन आउटलेयर प्रतीत नहीं होता है।

यह ध्यान दिया जाना चाहिए कि कुछ मामलों में, शोधकर्ता उन टिप्पणियों पर विचार करते हैं जिनके मानकीकृत अवशेष 2 के निरपेक्ष मान से अधिक हो जाते हैं।

आप जिस क्षेत्र में काम कर रहे हैं और जिस विशिष्ट समस्या पर आप काम कर रहे हैं, उसके आधार पर यह आप पर निर्भर करता है कि आप आउटलेर्स के लिए अपनी सीमा के रूप में 2 या 3 के पूर्ण मान का उपयोग करना चाहते हैं या नहीं।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल मानकीकृत अवशेषों के बारे में अतिरिक्त जानकारी प्रदान करते हैं:

सांख्यिकी में अवशेष क्या हैं?
एक्सेल में मानकीकृत अवशेषों की गणना कैसे करें
आर में मानकीकृत अवशेषों की गणना कैसे करें
पायथन में मानकीकृत अवशेषों की गणना कैसे करें