यहां बताया गया है कि f वितरण तालिका से p मान कैसे प्राप्त करें
एफ वितरण तालिका एक तालिका है जो एफ वितरण के महत्वपूर्ण मूल्यों को दर्शाती है। F वितरण तालिका का उपयोग करने के लिए, आपको केवल तीन मानों की आवश्यकता है:
- अंश की स्वतंत्रता की डिग्री
- हर की स्वतंत्रता की डिग्री
- अल्फ़ा स्तर
एफ वितरण का उपयोग अक्सर विचरण या संक्षेप में एनोवा के विश्लेषण में किया जाता है। उदाहरण के लिए, एनोवा से आउटपुट तालिका इस तरह दिख सकती है:
| स्रोत | एसएस | डीएफ | एमएस। | एफ | पी। |
|---|---|---|---|---|---|
| इलाज | 58.8 | 2 | 29.4 | 1.74 | 0.217 |
| गलती | 202.8 | 12 | 16.9 | ||
| कुल | 261.6 | 14 |
इस उदाहरण में, F सांख्यिकी के अंश में स्वतंत्रता की डिग्री 2 है, F सांख्यिकी के हर में स्वतंत्रता की डिग्री 12 है, और F सांख्यिकी स्वयं 1.74 है। आइए मान लें कि हमारे द्वारा उपयोग किया जाने वाला अल्फा स्तर 0.10 है। उपरोक्त तालिका में, हम देखते हैं कि इस F आँकड़े के लिए p-मान 0.217 है। चूँकि 0.217 अल्फा स्तर से ऊपर है, हम यह निष्कर्ष निकालेंगे कि यह एफ आँकड़ा सांख्यिकीय रूप से महत्वपूर्ण नहीं है।
यदि हम इसके बजाय एफ वितरण तालिका का उपयोग करना चाहते हैं, तो हम अल्फा = 0.10 के लिए एफ वितरण तालिका का उपयोग करेंगे। हम तालिका में महत्वपूर्ण मान का पता लगाएंगे जो 2 के अंश में स्वतंत्रता की डिग्री (तालिका में DF1 = 2) और 12 के हर में स्वतंत्रता की डिग्री (तालिका में DF2 = 12) से मेल खाता है और नोट करेगा कि यह मान 2.8068 है। .
चूँकि ANOVA तालिका से 1.74 का हमारा F आँकड़ा, F वितरण तालिका से 2.8068 के महत्वपूर्ण F मान से अधिक नहीं है, हम यह निष्कर्ष निकालेंगे कि F आँकड़ा 0.10 के अल्फा स्तर पर महत्वपूर्ण नहीं है।
F वितरण तालिका महत्वपूर्ण मान प्रदान करती है, P मान नहीं
उपरोक्त उदाहरण में ध्यान दें कि एफ वितरण तालिका हमें हमारे एफ आंकड़ों की तुलना करने के लिए एक महत्वपूर्ण एफ मान देती है। एफ वितरण तालिका हमें सीधे एपी मूल्य नहीं देती है।
यदि आपके पास अंश में स्वतंत्रता की डिग्री और हर में स्वतंत्रता की डिग्री के साथ एक एफ आँकड़ा है और आप संबंधित पी-मान ढूंढना चाहते हैं, तो आपको एफ वितरण कैलकुलेटर का उपयोग करने की आवश्यकता होगी।
उदाहरण के लिए, मान लीजिए कि हम जानते हैं कि हमारी एफ आँकड़ा 1.74 है, स्वतंत्रता की अंश डिग्री 2 हैं, और स्वतंत्रता की हर डिग्री 12 हैं और हम इस एफ आँकड़े के लिए पी-मान खोजना चाहते हैं। इस मामले में, हम दर्ज करेंगे एफ वितरण कैलकुलेटर में निम्नलिखित संख्याएँ:
नोट: अंतिम बॉक्स को खाली छोड़ दें. कैलकुलेटर स्वचालित रूप से आपके लिए यह मान ढूंढ लेगा।
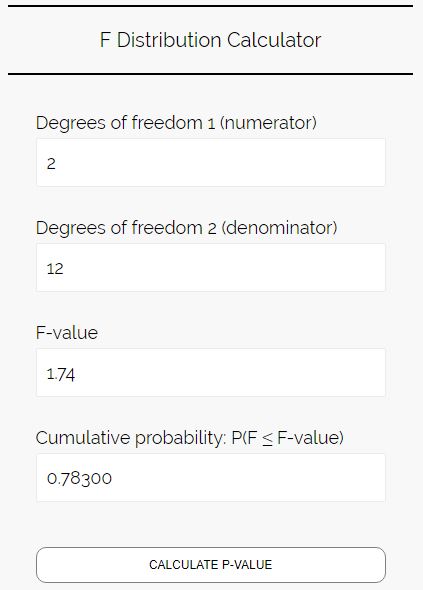
यह हमें बताता है कि संचयी संभावना 0.78300 है। यह एफ वितरण में एफ सांख्यिकी के बाईं ओर का क्षेत्र है। आमतौर पर हम एफ सांख्यिकी के दाईं ओर के क्षेत्र में रुचि रखते हैं, इसलिए इस मामले में पी-मान 1 – 0.78300 = 0.217 होगा।
एफ वितरण तालिका का उपयोग कब करें
यदि आप दिए गए अंश की स्वतंत्रता की डिग्री, हर की स्वतंत्रता की डिग्री और अल्फा स्तर के लिए महत्वपूर्ण मान एफ ढूंढना चाहते हैं, तो आपको एफ वितरण तालिका का उपयोग करने की आवश्यकता है।
इसके बजाय, यदि आपके पास दिए गए एफ आँकड़े (एनोवा या अन्य सांख्यिकीय परीक्षण से) हैं, जिसमें अंश की स्वतंत्रता की डिग्री और हर की स्वतंत्रता की डिग्री दी गई है और आप बस इस एफ आँकड़े का पी मान जानना चाहते हैं, तो आपको एक का उपयोग करने की आवश्यकता होगी ऐसा करने के लिए एफ वितरण कैलकुलेटर ।
लेखक के बारे में
डॉ. बेंजामिन एंडरसन
नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने