तीन परिकल्पनाएँ युग्मित टी परीक्षण में तैयार की गईं

युग्मित नमूने टी-परीक्षण का उपयोग दो नमूनों के माध्यों की तुलना करने के लिए किया जाता है जब एक नमूने में प्रत्येक अवलोकन को दूसरे नमूने में एक अवलोकन के साथ जोड़ा जा सकता है।

इस प्रकार का परीक्षण डेटा के बारे में निम्नलिखित धारणाएँ बनाता है:

1. स्वतंत्रता: प्रत्येक अवलोकन किसी भी अन्य अवलोकन से स्वतंत्र होना चाहिए।

2. सामान्यता: जोड़ियों के बीच अंतर लगभग सामान्य रूप से वितरित होना चाहिए।

3. कोई अत्यधिक आउटलेर्स नहीं: अंतरों में कोई अत्यधिक आउटलेर्स नहीं होना चाहिए।

यदि इनमें से एक या अधिक धारणाएँ पूरी नहीं होती हैं, तो युग्मित नमूनों के टी-परीक्षण के परिणाम अविश्वसनीय या भ्रामक हो सकते हैं।

इस ट्यूटोरियल में, हम प्रत्येक धारणा का स्पष्टीकरण प्रदान करते हैं, यह कैसे निर्धारित किया जाए कि धारणा पूरी हुई है या नहीं, और यदि इसका उल्लंघन होता है तो क्या करें।

परिकल्पना 1: स्वतंत्रता

एक युग्मित नमूना टी-परीक्षण मानता है कि प्रत्येक अवलोकन अन्य सभी अवलोकनों से स्वतंत्र है।

इस परिकल्पना को कैसे सत्यापित करें

इस धारणा को सत्यापित करने का सबसे सरल तरीका यह सत्यापित करना है कि प्रत्येक अवलोकन यादृच्छिक नमूनाकरण विधि का उपयोग करके एकत्र किया गया था।

यदि यादृच्छिक नमूनाकरण विधि का उपयोग किया गया था (जैसे कि सरल यादृच्छिक नमूनाकरण), तो हम मान सकते हैं कि प्रत्येक अवलोकन अन्य सभी अवलोकनों से स्वतंत्र है।

यदि इस धारणा का सम्मान न किया जाए तो क्या करें?

यदि यह धारणा पूरी नहीं होती है, तो युग्मित नमूने टी-परीक्षण के परिणाम पूरी तरह से अमान्य हैं।

इस परिदृश्य में, यह सुनिश्चित करने के लिए कि प्रत्येक अवलोकन स्वतंत्र है, यादृच्छिक नमूना पद्धति का उपयोग करके नए अवलोकन एकत्र करना सबसे अच्छा है।

परिकल्पना 2: सामान्यता

एक युग्मित नमूना टी-परीक्षण मानता है कि जोड़ियों के बीच अंतर लगभग सामान्य रूप से वितरित किया जाना चाहिए।

यह एक महत्वपूर्ण धारणा है क्योंकि यदि जोड़ियों के बीच अंतर सामान्य रूप से वितरित नहीं किया जाता है, तो निष्कर्ष निकालने के लिए परीक्षण के पी-वैल्यू का उपयोग करना मान्य नहीं है।

इस परिकल्पना को कैसे सत्यापित करें

इस परिकल्पना का परीक्षण करने का सबसे आसान तरीका बस युग्मित अंतरों का एक हिस्टोग्राम बनाना है और यह जांचना है कि हिस्टोग्राम में घंटी का आकार है या नहीं।

उदाहरण के लिए, यदि हिस्टोग्राम इस तरह दिखता है, तो हम कहेंगे कि सामान्यता की धारणा पूरी हो गई है:

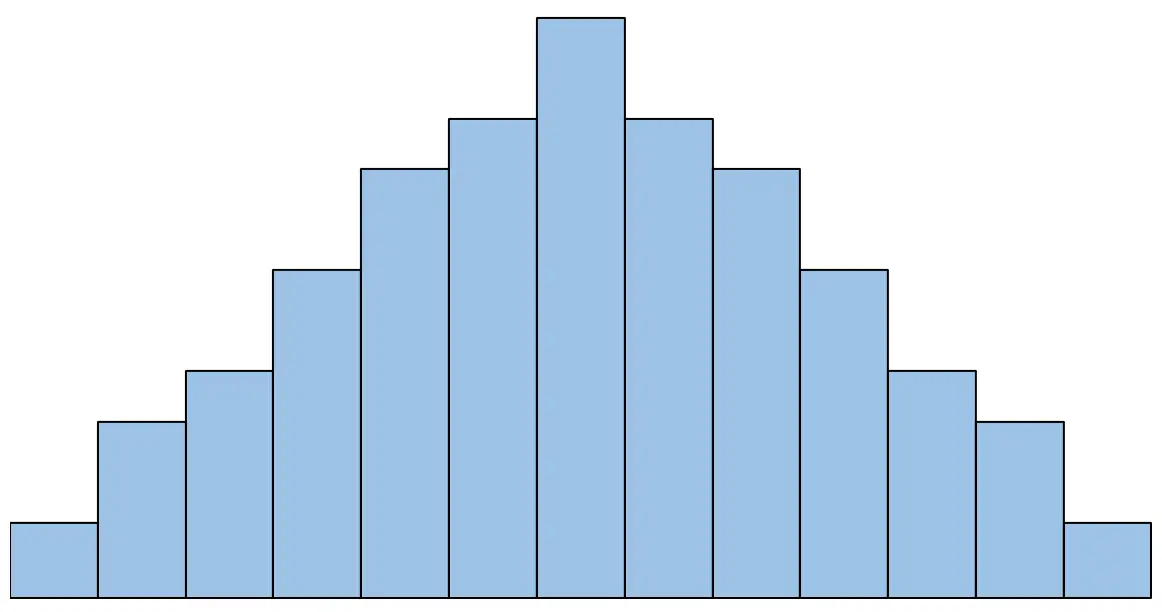
हालाँकि, यदि हिस्टोग्राम इस तरह दिखता है, तो हम कहेंगे कि सामान्यता की धारणा पूरी नहीं हुई है:

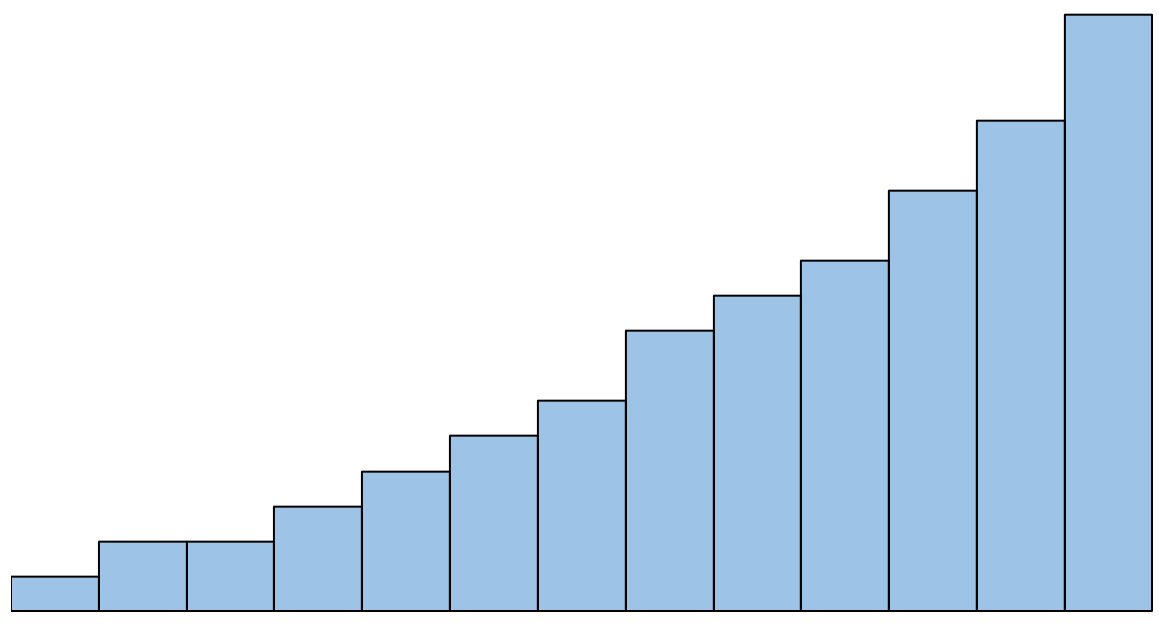
यदि इस धारणा का सम्मान न किया जाए तो क्या करें?

यदि इस धारणा का उल्लंघन किया जाता है, तो हम एक विलकॉक्सन हस्ताक्षरित-रैंक परीक्षण कर सकते हैं, जिसे युग्मित नमूने टी-टेस्ट के गैरपैरामीट्रिक समकक्ष माना जाता है और यह नहीं मानता कि युग्मित अंतर सामान्य रूप से वितरित होते हैं।

परिकल्पना 3: कोई चरम आउटलेर नहीं

एक युग्मित नमूना टी-परीक्षण मानता है कि डेटा में कोई चरम आउटलेर नहीं हैं।

इस परिकल्पना को कैसे सत्यापित करें

इस परिकल्पना का परीक्षण करने का सबसे आसान तरीका युग्मित अंतरों का एक बॉक्स प्लॉट बनाना और दृष्टिगत रूप से जांचना है कि क्या कोई बाहरी कारक हैं।

उदाहरण के लिए, मान लीजिए कि युग्मित अंतरों का बॉक्स प्लॉट इस तरह दिखता है:

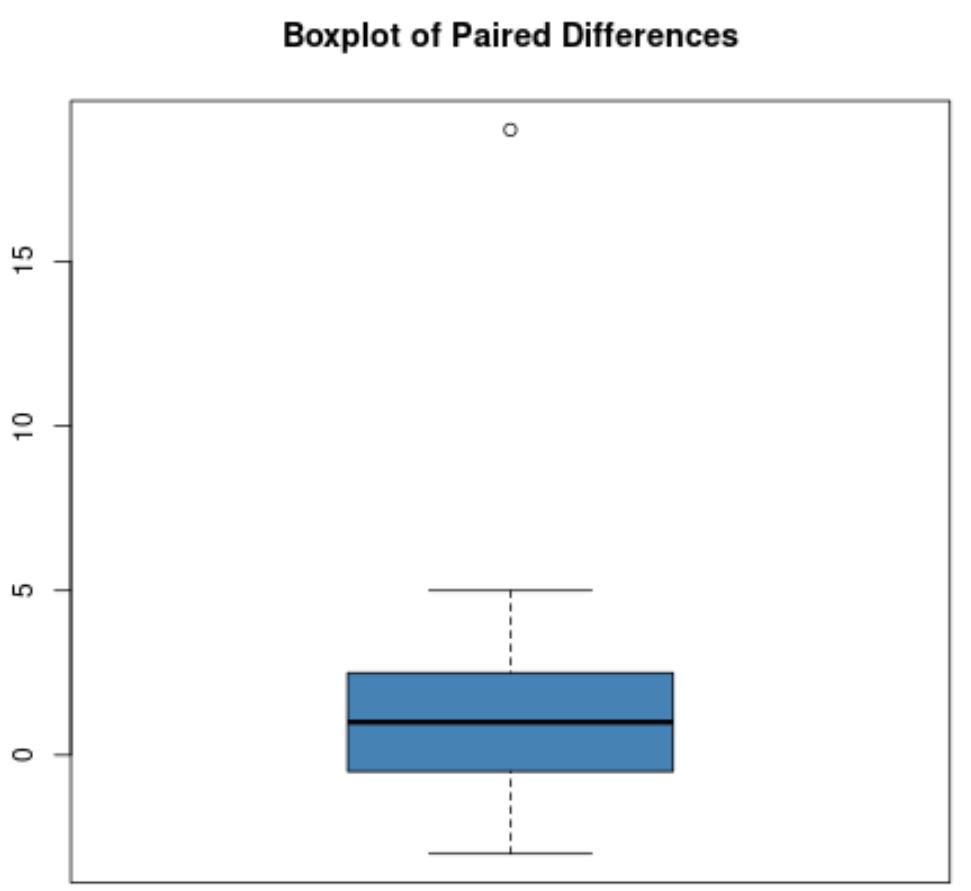
अधिकांश युग्मित अंतर शून्य के करीब हैं, लेकिन एक युग्मित अंतर लगभग 19 के बराबर है, जो स्पष्ट रूप से एक बाहरी अंतर है।

ध्यान दें : एक सर्कल का उपयोग आम तौर पर एक बॉक्स प्लॉट में बाहरी को इंगित करने के लिए किया जाता है।

हालाँकि, मान लीजिए कि युग्मित अंतरों का बॉक्स प्लॉट इस तरह दिखता है:

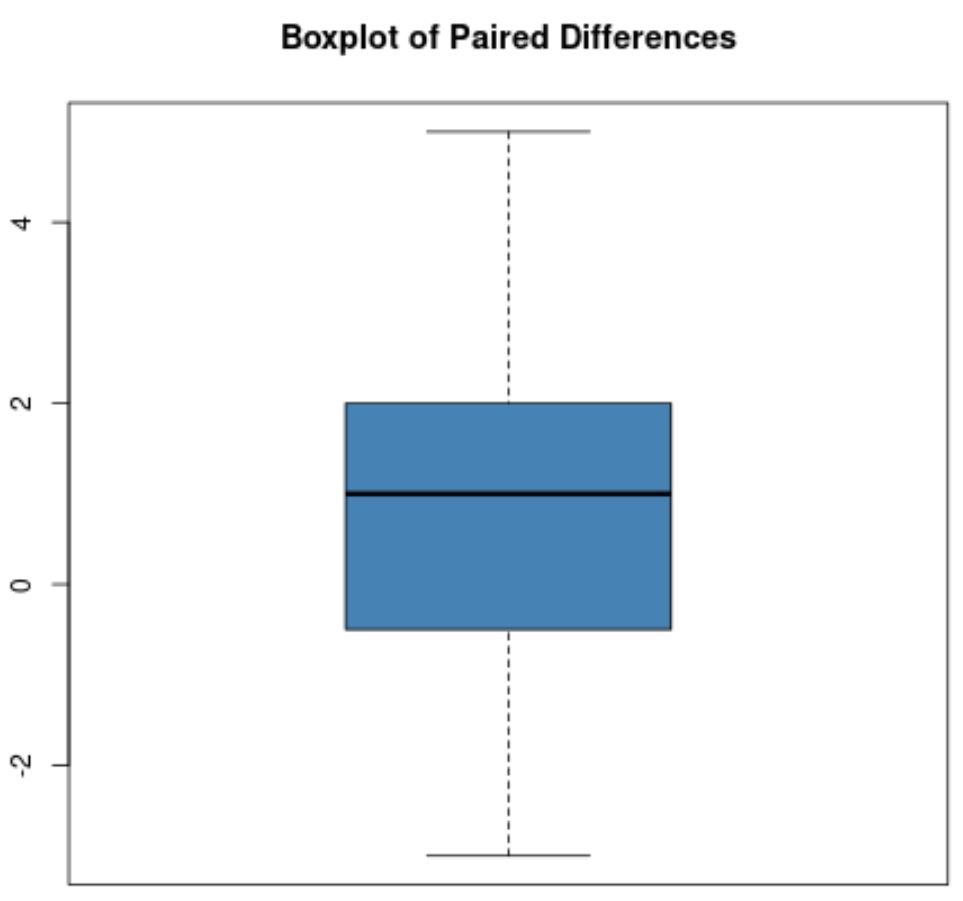
इस बॉक्सप्लॉट में कोई स्पष्ट आउटलेयर नहीं हैं, इसलिए हम मान लेंगे कि डेटा में कोई अत्यधिक आउटलेयर नहीं हैं।

यदि इस धारणा का सम्मान न किया जाए तो क्या करें?

यदि इस धारणा का उल्लंघन किया जाता है, तो युग्मित नमूनों के टी-परीक्षण के परिणाम असामान्य रूप से प्रभावित हो सकते हैं।

इस परिदृश्य में, यदि आपको लगता है कि यह एक दोषपूर्ण डेटा बिंदु का प्रतिनिधित्व करता है या डेटा प्रविष्टि त्रुटि का परिणाम है, तो आप आउटलेयर को हटा सकते हैं।

वैकल्पिक रूप से, आप बाहरी को रख सकते हैं और युग्मित-नमूने टी-परीक्षण परिणामों की रिपोर्ट करते समय इसे आसानी से नोट कर सकते हैं।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल अन्य सांख्यिकीय परीक्षणों में की गई धारणाओं की व्याख्या करते हैं:

परीक्षण में चार परिकल्पनाएँ तैयार की गईं
काई-स्क्वायर परीक्षण की चार परिकल्पनाएँ
पैरामीट्रिक परीक्षणों की चार परिकल्पनाएँ