वृत्ताकार आरेख

इस लेख में, आप सीखेंगे कि पाई चार्ट क्या है, पाई चार्ट कैसे बनाएं और इस प्रकार के चार्ट के लिए चरण-दर-चरण अभ्यास करें। इसके अलावा, आप देख पाएंगे कि पाई चार्ट की विशेषताएं क्या हैं।

पाई चार्ट क्या है?

पाई चार्ट , जिसे पाई चार्ट भी कहा जाता है, एक प्रकार का सांख्यिकीय चार्ट है जिसका उपयोग प्रतिशत और अनुपात को दृश्य रूप से दर्शाने के लिए किया जाता है। अधिक सटीक रूप से, पाई चार्ट में, डेटा को एक वृत्त के भागों द्वारा दर्शाया जाता है, ताकि प्रत्येक चीज़ का कोण उसकी आवृत्ति के समानुपाती हो।

इसलिए, किसी मूल्य की आवृत्ति जितनी अधिक होगी, पाई चार्ट में उसका हिस्सा उतना ही अधिक होगा।

आंकड़ों में, ग्राफ़ पर गुणात्मक डेटा का प्रतिनिधित्व करने के लिए पाई चार्ट बहुत उपयोगी होते हैं, और वे आपको तुरंत निष्कर्ष निकालने की अनुमति भी देते हैं।

यह ध्यान दिया जाना चाहिए कि पाई चार्ट के कई अलग-अलग नाम हैं जैसे पाई चार्ट, पिज़्ज़ा चार्ट, पाई चार्ट, चीज़ चार्ट या यहां तक कि 360 डिग्री चार्ट।

पाई चार्ट कैसे बनाये

पाई चार्ट की परिभाषा को देखते हुए, यह अनुभाग दिखाता है कि इस प्रकार का चार्ट कैसे बनाया जाए:

1. सांख्यिकीय डेटा एकत्र करें और संबंधित आवृत्ति तालिका तैयार करें।
2. निम्नलिखित सूत्र से ग्राफ़ के प्रत्येक त्रिज्यखंड के कोण की गणना करें



सोना



सेक्टर I का कोण है,



इसकी पूर्ण आवृत्ति और



डेटा की कुल संख्या.

3. परिकलित कोणों से, एक प्रोट्रैक्टर का उपयोग करके एक गोलाकार ग्राफ़ पर सेक्टरों का प्रतिनिधित्व करें।
4. निम्नलिखित सूत्र से प्रत्येक सेक्टर के प्रतिशत की गणना करें:



सोना



सेक्टर I का प्रतिशत है,



इसकी पूर्ण आवृत्ति और



डेटा की कुल संख्या.

5. ग्राफ़ पर प्रत्येक सेक्टर का प्रतिशत इंगित करें।

पाई चार्ट उदाहरण

ताकि आप देख सकें कि एक गोलाकार चार्ट कैसे बनाया जाता है, मैं आपको नीचे चरण दर चरण समझाया गया एक उदाहरण छोड़ता हूँ।

• 50 लोगों से उनके पसंदीदा शहर के बारे में पूछा गया और डेटा को निम्नलिखित तालिका में संकलित किया गया। इस सांख्यिकीय डेटा को पाई चार्ट पर प्लॉट करें।

सबसे पहले आपको वह कोण ढूंढना होगा जो प्रत्येक चीज़ से मेल खाता है। ऐसा करने के लिए, हम निम्नलिखित सूत्र लागू करते हैं:

उदाहरण के तौर पर, डेटा तालिका में पहले मान के अनुरूप कोण की गणना की जाती है:

एक बार जब हम कोण जान लेते हैं, तो बस एक चांदे का उपयोग करके वृत्ताकार क्षेत्र का प्रतिनिधित्व करें:

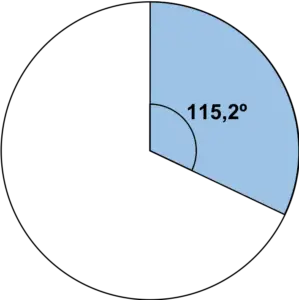
हम तालिका में सभी मानों के लिए वही चरण दोहराते हैं:

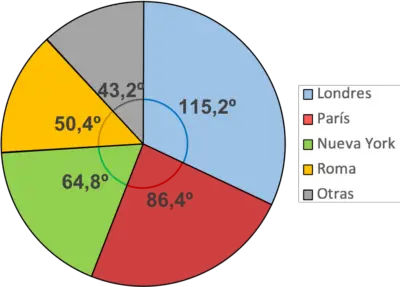
ग्राफ़ को समझने में आसान बनाने के लिए प्रत्येक सेक्टर को एक रंग में रंगने की अनुशंसा की जाती है। इसी तरह, आपको आरेख में प्रत्येक रंग का अर्थ दिखाने के लिए एक किंवदंती जोड़नी चाहिए।

चीज़ों का रेखांकन करने के बाद, हमें इसे आरेख पर रखने के लिए प्रत्येक के प्रतिशत की गणना करने की आवश्यकता है। ऐसा करने के लिए, हम निम्नलिखित सूत्र का उपयोग करते हैं:

इसलिए प्रत्येक क्षेत्र का प्रतिशत है:

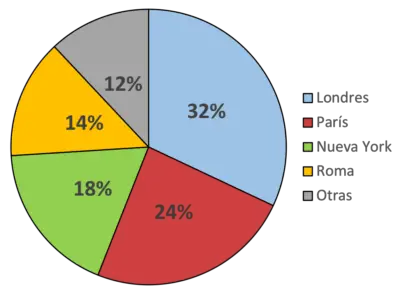
इस पाई चार्ट के साथ हम इंगित करते हैं कि, उदाहरण के लिए, नीला रंग लंदन शहर का प्रतिनिधित्व करता है और वह स्थान है जिसे अधिकांश लोग पसंद करते हैं (32% लोग)। दूसरी ओर, हरा रंग न्यूयॉर्क का प्रतिनिधित्व करता है, जो सर्वेक्षण में शामिल 18% लोगों का पसंदीदा शहर है।

पाई चार्ट सुविधाएँ

कैमेम्बर्ट की विशेषताएं इस प्रकार हैं:

• गुणात्मक डेटा प्रस्तुत करने के लिए पाई चार्ट बहुत उपयोगी है।
• हालाँकि, अन्य प्रकार के सांख्यिकीय ग्राफ़ भी हैं जो मात्रात्मक चर या समय श्रृंखला का प्रतिनिधित्व करने के लिए अधिक उपयुक्त हैं।
• इसके अतिरिक्त, पाई चार्ट में केवल एक चर का प्रतिनिधित्व किया जा सकता है, जिससे चर की तुलना करना मुश्किल हो जाता है।
• पाई चार्ट बहुत ही दृश्यमान है, जो त्वरित विश्लेषण और निष्कर्ष की अनुमति देता है।
• जब कई सेक्टर हों या कुछ बहुत छोटे हों तो चार्ट को पढ़ना मुश्किल होता है। ऐसे मामले में, छोटे क्षेत्रों को “अन्य” नामक एक एकल क्षेत्र में समूहित करने की सिफारिश की जाती है।