शून्य क्रम सहसंबंध क्या है?

आंकड़ों में, दो चरों के बीच का सहसंबंध हमें इन दो चरों के बीच संबंध के बारे में बताता है।

सहसंबंध के सबसे बुनियादी प्रकारों में से एक को शून्य-क्रम सहसंबंध के रूप में जाना जाता है, जो अन्य चर के संभावित प्रभाव को नियंत्रित किए बिना दो चर के बीच सहसंबंध को संदर्भित करता है।

इस प्रकार के सहसंबंध का एक उदाहरण पियर्सन सहसंबंध गुणांक है, जो दो चर के बीच रैखिक संबंध को मापता है और -1 और 1 के बीच मान ले सकता है जहां:

• -1 दो चरों के बीच पूर्णतः नकारात्मक रैखिक सहसंबंध दर्शाता है
• 0 दो चरों के बीच कोई रैखिक सहसंबंध नहीं दर्शाता है
• 1 दो चरों के बीच पूर्णतः सकारात्मक रैखिक सहसंबंध दर्शाता है

सहसंबंध शून्य से जितना अधिक होगा, दोनों चरों के बीच संबंध उतना ही मजबूत होगा।

पहले और दूसरे क्रम के सहसंबंध

यदि हम तीसरे चर C के प्रभाव को नियंत्रित करते हुए दो चर A और B के बीच सहसंबंध की गणना करते हैं, तो हम A और B के बीच सहसंबंध को प्रथम-क्रम सहसंबंध कहेंगे।

इसी प्रकार, यदि हम चर C और D के प्रभाव को नियंत्रित करते हुए दो चर A और B के बीच सहसंबंध की गणना करते हैं, तो हम A और B के बीच सहसंबंध को दूसरे क्रम का सहसंबंध कहेंगे।

शून्य-क्रम सहसंबंध उदाहरण

मान लीजिए कि हमारे पास निम्नलिखित डेटा सेट है जो 10 अलग-अलग छात्रों द्वारा अध्ययन में बिताए गए घंटों और परीक्षा में प्राप्त ग्रेड को दर्शाता है:

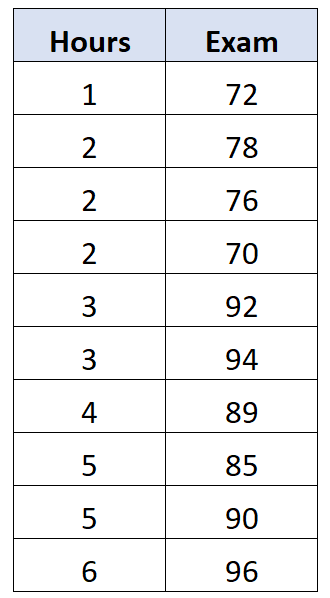
इससे पता चलता है कि इन दोनों चरों के बीच सहसंबंध 0.762 है। इसे दो चरों के बीच शून्य-क्रम सहसंबंध माना जाएगा, क्योंकि हम तीसरे चर के संभावित प्रभाव को नियंत्रित नहीं करते हैं।

हालाँकि, वास्तव में, यह संभव है कि अन्य कारक इन दो चरों के बीच संबंध को प्रभावित करें।

उदाहरण के लिए, कक्षा में छात्र के वर्तमान ग्रेड का उनके परीक्षा स्कोर पर प्रभाव पड़ सकता है। मान लीजिए कि हमारे पास भी इस डेटा तक पहुंच है:

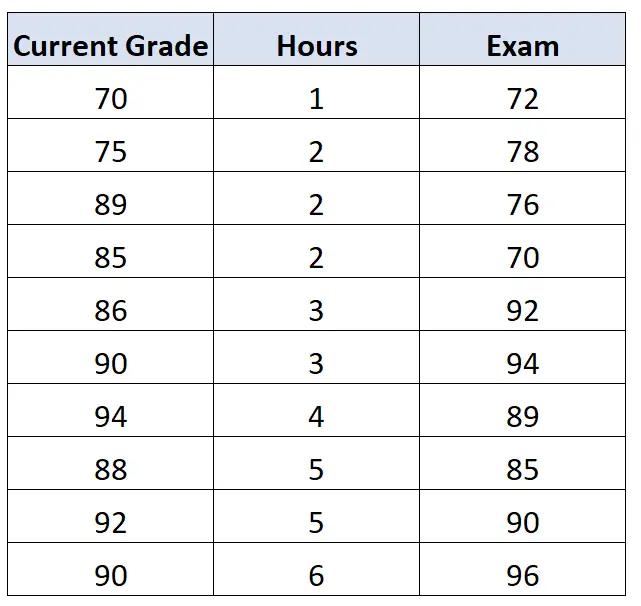
यदि हमने वर्तमान ग्रेड के प्रभाव को नियंत्रित करते हुए घंटों और परीक्षा के बीच सहसंबंध की गणना की, तो हम पाएंगे कि घंटों और परीक्षा के बीच प्रथम-क्रम सहसंबंध 0.578 है।

इसका मतलब यह है कि कक्षा में छात्र के वर्तमान ग्रेड के प्रभाव को नियंत्रित करने के बाद भी, अध्ययन किए गए घंटों और परीक्षा ग्रेड के बीच काफी मजबूत सकारात्मक सहसंबंध है।

नोट: प्रथम-क्रम सहसंबंध को कभी-कभी आंशिक सहसंबंध भी कहा जाता है । यह ट्यूटोरियल बताता है कि एक्सेल में आंशिक सहसंबंधों की गणना कैसे करें।

सहसंबंध मैट्रिक्स में शून्य-क्रम सहसंबंध

हम एक सहसंबंध मैट्रिक्स बनाते हैं जब भी चर के एक सेट के लिए, मैट्रिक्स में प्रदर्शित सहसंबंध गुणांक हमेशा शून्य-क्रम सहसंबंध होते हैं क्योंकि वे अन्य चर के प्रभाव पर विचार किए बिना केवल चर के प्रत्येक जोड़ीदार संयोजन के बीच सहसंबंध होते हैं।

उदाहरण के लिए, पिछले उदाहरण से हमारे डेटासेट पर विचार करें:

यदि हमने इस डेटासेट के लिए सहसंबंध मैट्रिक्स बनाया है, तो यह इस तरह दिखेगा:

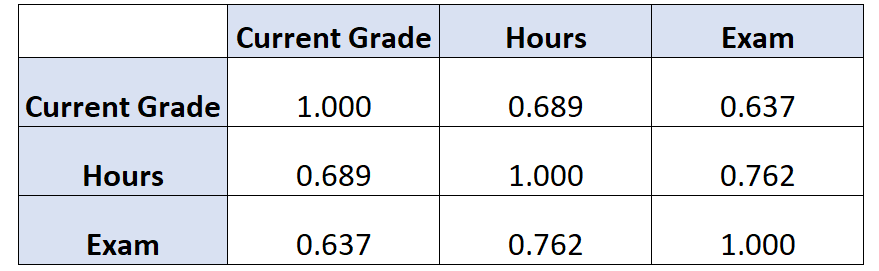
इसकी व्याख्या करने का तरीका यह है:

• वर्तमान ग्रेड और अध्ययन किए गए घंटों के बीच सहसंबंध 0.689 है।
• वर्तमान स्कोर और परीक्षा में प्राप्त स्कोर के बीच संबंध 0.637 है।
• अध्ययन के घंटों और परीक्षा स्कोर के बीच संबंध 0.762 है।

इनमें से प्रत्येक सहसंबंध एक शून्य-क्रम सहसंबंध है।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल सहसंबंध गुणांक के बारे में अतिरिक्त जानकारी प्रदान करते हैं:

पियर्सन सहसंबंध गुणांक का परिचय
सहसंबंध मैट्रिक्स कैसे पढ़ें
एक्सेल में आंशिक सहसंबंध की गणना कैसे करें