सहसम्बंध मैट्रिक्स

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 5, 2023 आंकड़े शून्य टिप्पणियां

इस लेख में आप जानेंगे कि सहसंबंध मैट्रिक्स क्या है, इसका सूत्र क्या है और सहसंबंध मैट्रिक्स की व्याख्या कैसे करें। इसके अतिरिक्त, आप सहसंबंध मैट्रिक्स की व्याख्या का एक ठोस उदाहरण देख पाएंगे।

सहसंबंध मैट्रिक्स क्या है?

सहसंबंध मैट्रिक्स एक मैट्रिक्स है जिसमें स्थिति i,j में चर i और j के बीच सहसंबंध गुणांक होता है।

इसलिए, सहसंबंध मैट्रिक्स एक वर्ग मैट्रिक्स है जो मुख्य विकर्ण पर लोगों से भरा होता है और पंक्ति i और कॉलम j के तत्व में चर i और चर j के बीच सहसंबंध गुणांक का मान होता है।

इसलिए सहसंबंध मैट्रिक्स का सूत्र इस प्रकार है:

सोना

$r_{ij}$

चरों के बीच सहसंबंध गुणांक है

$i$

और

$j.$

इसलिए, किसी डेटा सेट के सहसंबंध मैट्रिक्स को खोजने के लिए, यह आवश्यक है कि आप जानें कि सहसंबंध गुणांक की गणना कैसे की जाती है। यदि आपको याद नहीं है, तो निम्नलिखित लिंक में आप जानेंगे कि इसे ऑनलाइन कैलकुलेटर के साथ कैसे करें:

➤ देखें: सहसंबंध गुणांक कैलकुलेटर

सहसंबंध गुणांक का एक गुण यह है कि इसकी गणना के लिए चरों का क्रम अर्थात सहसंबंध गुणांक मायने नहीं रखता

$r_{ij}$

के बराबर है

$r_{ji}.$

इसलिए, सहसंबंध मैट्रिक्स सममित है।

$\displaystyle R=\begin{pmatrix}1&r_{12}&r_{13}&\dots&r_{1n}\\[1.1ex] r_{12}&1&r_{23}&\dots&r_{2n}\\[1.1ex] r_{13}&r_{23}&1&\dots&r_{3n}\\[1.1ex] \vdots &\vdots &\vdots &\ddots &\vdots\\[1.1ex] r_{1n}&r_{2n}&r_{3n}&\dots&1\end{pmatrix}$

सहसंबंध मैट्रिक्स के सार्थक होने के लिए, सांख्यिकीय डेटा सेट में दो से अधिक चर होने चाहिए। अन्यथा, यह एकल सहसंबंध गुणांक निर्धारित करने के लिए पर्याप्त होगा और सहसंबंध मैट्रिक्स सार्थक होगा।

सहसंबंध मैट्रिक्स कैसे बनाएं

सहसंबंध मैट्रिक्स की परिभाषा को देखते हुए, आइए देखें कि इस प्रकार का सांख्यिकीय मैट्रिक्स कैसे बनाया जाता है:

चरों के प्रत्येक जोड़े के सहसंबंध गुणांक की गणना करें। ध्यान दें कि चरों का क्रम परिणाम को नहीं बदलता है, इसलिए चरों के प्रत्येक जोड़े के लिए इसे केवल एक बार गणना करने की आवश्यकता होती है।
डेटा श्रृंखला में चरों की संख्या के समान आयाम का एक वर्ग मैट्रिक्स बनाएं। यह मैट्रिक्स सहसंबंध मैट्रिक्स होगा.
सहसंबंध मैट्रिक्स के मुख्य विकर्ण के प्रत्येक तत्व में 1 लगाएं।
चर i , j के सहसंबंध गुणांक को i , j और j , i स्थिति में रखें।
एक बार सहसंबंध मैट्रिक्स बन जाने के बाद, जो कुछ बचा है वह इसके मूल्यों की व्याख्या करना है।

ध्यान रखें कि केवल सहसंबंध मैट्रिक्स को चलाना पर्याप्त नहीं है, फिर आपको इसके मूल्यों की व्याख्या करने और समझने की आवश्यकता है कि उनका क्या मतलब है। निम्नलिखित अनुभाग बताता है कि सहसंबंध मैट्रिक्स की व्याख्या कैसे करें।

सहसंबंध मैट्रिक्स की व्याख्या

सहसंबंध मैट्रिक्स की सही व्याख्या करने के लिए, यह ध्यान रखना आवश्यक है कि सहसंबंध गुणांक का मान -1 से +1 तक हो सकता है:

r=-1 : दो चरों का पूर्ण नकारात्मक सहसंबंध है, इसलिए हम एक नकारात्मक ढलान वाली एक रेखा खींच सकते हैं जिसमें सभी बिंदु जुड़ते हैं।
-1<r<0 : दो चरों के बीच सहसंबंध नकारात्मक है, इसलिए जब एक चर बढ़ता है तो दूसरा घटता है। मान -1 के जितना करीब होगा, चर उतने ही अधिक नकारात्मक रूप से संबंधित होंगे।
r=0 : दो चरों के बीच सहसंबंध बहुत कमजोर है, वास्तव में, उनके बीच रैखिक संबंध शून्य है। इसका मतलब यह नहीं है कि चर स्वतंत्र हैं, क्योंकि उनका गैर-रैखिक संबंध हो सकता है।
0<r<1 : दो चरों के बीच सहसंबंध सकारात्मक है, मान +1 के जितना करीब होगा, चरों के बीच संबंध उतना ही मजबूत होगा। इस मामले में, जब दूसरा भी बढ़ता है तो एक चर का मान बढ़ने लगता है।
r=1 : दो चरों का पूर्ण सकारात्मक सहसंबंध है, अर्थात उनका सकारात्मक रैखिक संबंध है।

इस प्रकार, सहसंबंध मैट्रिक्स की व्याख्या करने के लिए, प्रत्येक सहसंबंध गुणांक की व्याख्या करना और विभिन्न परिणामों की तुलना करना आवश्यक है।

इस तरह आप यह देख पाएंगे कि कौन से चर एक-दूसरे से सबसे अधिक संबंधित हैं, कौन से चर सबसे महत्वपूर्ण हैं, किन चर का एक-दूसरे के साथ व्यावहारिक रूप से कोई संबंध नहीं है, आदि।

सहसंबंध मैट्रिक्स उदाहरण

पूरी तरह से समझने के लिए कि सहसंबंध मैट्रिक्स में क्या शामिल है और इसकी व्याख्या कैसे की जाती है, इस खंड में हम सहसंबंध मैट्रिक्स के एक उदाहरण का विश्लेषण करेंगे:

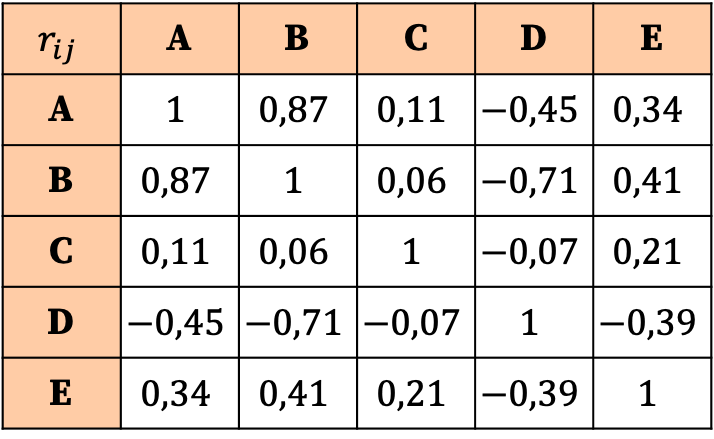
सहसंबंध मैट्रिक्स की व्याख्या गुणांक के मूल्यों पर आधारित है। इस प्रकार, हम देख सकते हैं कि सबसे मजबूत सहसंबंध चर ए और चर बी के बीच का संबंध है, क्योंकि इसका संबंधित गुणांक सबसे बड़ा (0.87) है।

दूसरी ओर, चर C का व्यावहारिक रूप से किसी भी चर के साथ कोई संबंध नहीं है, क्योंकि इसके सभी गुणांक शून्य के बहुत करीब हैं और इसलिए बहुत कम हैं। इस प्रकार, विश्लेषण को सरल बनाने के लिए, हम सांख्यिकीय अध्ययन से इस चर को हटाने पर भी विचार कर सकते हैं।

इसी प्रकार, वेरिएबल डी के अन्य वेरिएबल्स के साथ सभी संबंध नकारात्मक हैं, जिसका अर्थ है कि वेरिएबल डी और अन्य वेरिएबल्स के बीच सहसंबंध उलटा है। इसका मतलब यह नहीं है कि चर को समाप्त कर दिया जाना चाहिए, बस चर डी नकारात्मक रूप से सहसंबद्ध है।

जैसा कि आप देख सकते हैं, सहसंबंध मैट्रिक्स डेटा को सारांशित करने और डेटासेट में विभिन्न चर के बीच संबंधों का समग्र विश्लेषण करने के लिए बहुत उपयोगी है।

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने