सापेक्ष आवृत्ति
इस लेख में आप सीखेंगे कि आंकड़ों में सापेक्ष आवृत्ति क्या है, सापेक्ष आवृत्ति कैसे प्राप्त करें और सापेक्ष आवृत्ति पर चरण दर चरण दो हल किए गए अभ्यास।
सापेक्ष आवृत्ति क्या है?
आंकड़ों में, सापेक्ष आवृत्ति एक माप है जो इंगित करता है कि डेटा नमूने में कोई मान अनुपात या प्रतिशत के रूप में कितनी बार दिखाई देता है। अधिक सटीक रूप से, सापेक्ष आवृत्ति डेटा की कुल संख्या से विभाजित पूर्ण आवृत्ति के बराबर होती है।
उदाहरण के लिए, यदि किसी मान की पूर्ण आवृत्ति 15 है और कुल 100 डेटा बिंदु हैं, तो उस मान की सापेक्ष आवृत्ति 0.15 (15/100=0.15) है।
आम तौर पर, प्रतीक h i का उपयोग सापेक्ष आवृत्ति को दर्शाने के लिए किया जाता है। हालाँकि सांख्यिकीय समुदाय में अभी भी कोई सहमति नहीं है, इसलिए आप किसी अन्य प्रतीक द्वारा दर्शाई गई सापेक्ष आवृत्ति देख सकते हैं।
सापेक्ष आवृत्ति की गणना कैसे करें
सापेक्ष आवृत्ति डेटा की कुल संख्या से विभाजित पूर्ण आवृत्ति के बराबर होती है। इसलिए, सापेक्ष आवृत्ति की गणना करने के लिए, आपको पहले पूर्ण आवृत्ति ज्ञात करनी होगी और फिर इसे अवलोकनों की कुल संख्या से विभाजित करना होगा।
तो, सापेक्ष आवृत्ति का सूत्र इस प्रकार है:
![]()
सोना:
-
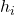
सापेक्ष आवृत्ति है.
-

पूर्ण आवृत्ति है.
-

डेटा की कुल संख्या है.
दूसरी ओर, प्रतिशत में सापेक्ष आवृत्ति की गणना करने के लिए, यानी प्रतिशत के रूप में व्यक्त सापेक्ष आवृत्ति, बस पिछले सूत्र को 100 से गुणा करें:
![]()
सापेक्ष आवृत्ति के उदाहरण
एक बार जब आप सापेक्ष आवृत्ति की परिभाषा देख लेंगे, तो नीचे वास्तविक दुनिया के दो उदाहरण दिए गए हैं ताकि आप देख सकें कि इस प्रकार की आवृत्ति की गणना कैसे की जाती है। पहले उदाहरण में, एक असतत चर की सापेक्ष आवृत्ति निर्धारित की जाती है और दूसरे उदाहरण में, एक सतत चर की।
उदाहरण 1: असतत चर
- 30 छात्रों की एक कक्षा में सांख्यिकी विषय में प्राप्त ग्रेड इस प्रकार हैं। प्रत्येक नोट की सापेक्ष आवृत्ति क्या है?
![]()
![]()
![]()
इस अभ्यास में चर असतत है क्योंकि डेटा केवल पूर्णांक हो सकता है; इसलिए, डेटा को अंतरालों में समूहित करने की कोई आवश्यकता नहीं है।
सापेक्ष आवृत्ति ज्ञात करने के लिए, हमें पहले पूर्ण आवृत्ति निर्धारित करनी होगी। इसलिए हम एक आवृत्ति तालिका बनाते हैं और प्रत्येक भिन्न मान के लिए पूर्ण आवृत्ति की गणना करते हैं:

अब जबकि हमने निरपेक्ष आवृत्ति की गणना कर ली है, हम सापेक्ष आवृत्ति की गणना कर सकते हैं। ऐसा करने के लिए, बस प्रत्येक पूर्ण आवृत्ति को डेटा की कुल संख्या (30) से विभाजित करें:
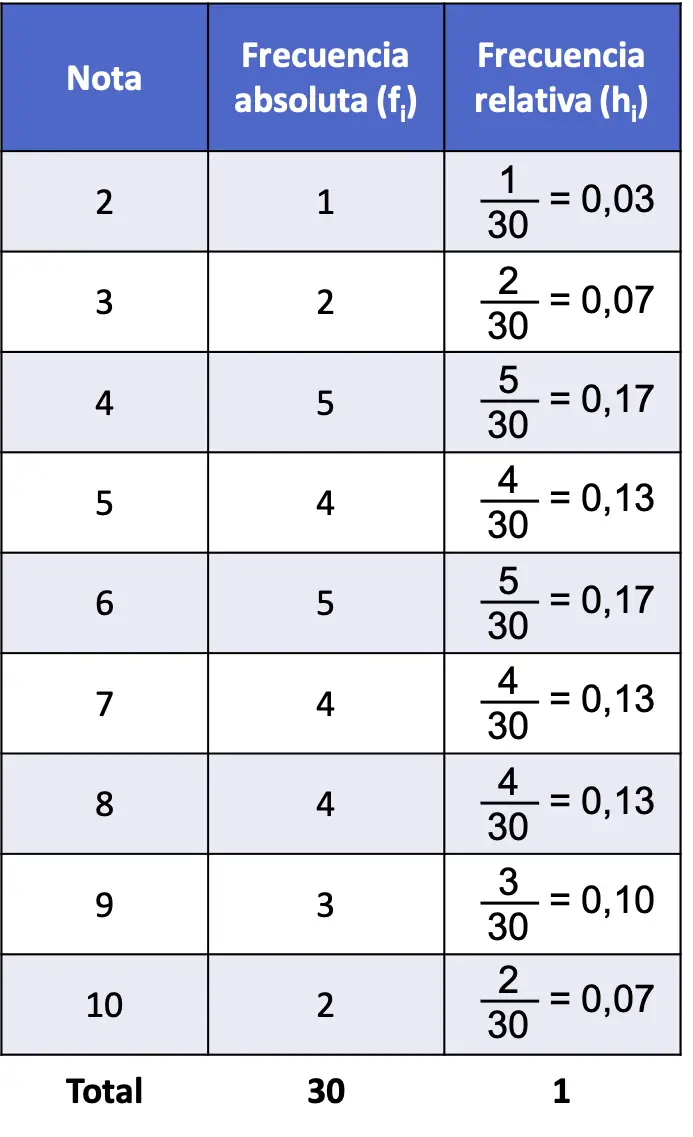
तो, निरपेक्ष आवृत्ति और सापेक्ष आवृत्ति के साथ समस्या की आवृत्ति तालिका इस प्रकार है:

ध्यान दें कि सभी सापेक्ष आवृत्तियों का योग हमेशा 1 देता है, अन्यथा इसका मतलब है कि कुछ गणनाएँ गलत हैं।
उदाहरण 2: सतत चर
- 20 लोगों की ऊंचाई मापी गई और नीचे दिए गए परिणाम प्राप्त किए गए। डेटा को अंतरालों में अलग करें और प्रत्येक अंतराल की सापेक्ष आवृत्ति ज्ञात करें।
![]()
![]()
इस सांख्यिकीय नमूने में डेटा एक सतत चर से संबंधित है, क्योंकि वे दशमलव हैं और इसलिए चर कोई भी मान ले सकता है। इसलिए आवृत्ति गणना करने से पहले, हम पहले डेटा को 10 दसवें के आयाम के साथ अंतराल में समूहित करेंगे।
इसके बाद, हम प्रत्येक अंतराल की पूर्ण आवृत्ति के साथ एक आवृत्ति तालिका बनाते हैं:

और एक बार जब हमें पूर्ण आवृत्ति मिल जाती है, तो हम प्रत्येक अंतराल की सापेक्ष आवृत्ति को उसकी पूर्ण आवृत्ति को डेटा की कुल संख्या (20) से विभाजित करके प्राप्त कर सकते हैं:

संचयी सापेक्ष आवृत्ति
जैसा कि नाम से पता चलता है, संचयी सापेक्ष आवृत्ति एक अन्य प्रकार की आवृत्ति है जिसका उपयोग आंकड़ों में किया जाता है और सापेक्ष आवृत्ति से गणना की जाती है।
अधिक सटीक रूप से, किसी मान की संचयी सापेक्ष आवृत्ति स्वयं मूल्य की सापेक्ष आवृत्ति और सभी छोटे मानों की सापेक्ष आवृत्तियों के योग के बराबर होती है।
ताकि आप देख सकें कि संचयी सापेक्ष आवृत्ति कैसे प्राप्त की जाती है, पहले उदाहरण में डेटासेट की संचयी सापेक्ष आवृत्ति की गणना नीचे की गई है:
