सामान्य वितरण

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 3, 2023 संभावना शून्य टिप्पणियां

यह आलेख बताता है कि सांख्यिकी में सामान्य वितरण क्या है। तो, आपको सामान्य वितरण की परिभाषा, सामान्य वितरण के उदाहरण और सामान्य वितरण के गुण क्या हैं, यह पता चलेगा।

सामान्य वितरण क्या है?

सामान्य वितरण एक सतत संभाव्यता वितरण है जिसका ग्राफ़ घंटी के आकार का और इसके माध्य के बारे में सममित है। आंकड़ों में, सामान्य वितरण का उपयोग बहुत भिन्न विशेषताओं वाली घटनाओं को मॉडल करने के लिए किया जाता है, यही कारण है कि यह वितरण इतना महत्वपूर्ण है।

वास्तव में, आंकड़ों में, सामान्य वितरण को अब तक सभी संभाव्यता वितरणों का सबसे महत्वपूर्ण वितरण माना जाता है, क्योंकि यह न केवल बड़ी संख्या में वास्तविक दुनिया की घटनाओं को मॉडल कर सकता है, बल्कि सामान्य वितरण का उपयोग अन्य प्रकार के अनुमान लगाने के लिए भी किया जा सकता है। वितरण. खास शर्तों के अन्तर्गत।

सामान्य वितरण का प्रतीक बड़े अक्षर N है। इसलिए, यह इंगित करने के लिए कि एक चर एक सामान्य वितरण का अनुसरण करता है, इसे अक्षर N द्वारा दर्शाया जाता है और इसके अंकगणितीय माध्य और मानक विचलन के मान कोष्ठक में जोड़े जाते हैं।

$X\sim N(\mu,\sigma)$

सामान्य वितरण के कई अलग-अलग नाम हैं, जिनमें गाऊसी वितरण , गाऊसी वितरण और लाप्लास-गॉस वितरण शामिल हैं।

सामान्य वितरण के उदाहरण

आमतौर पर, सामान्य वितरण का पालन करने वाले डेटासेट में बड़ी संख्या में अवलोकन होते हैं और बहुत सामान्य विषयों को कवर किया जाता है। नीचे सांख्यिकीय नमूनों के कई उदाहरण दिए गए हैं जिन्हें आम तौर पर सामान्य वितरण के साथ मॉडल किया जा सकता है।

सामान्य वितरण के उदाहरण:

किसी पाठ्यक्रम में विद्यार्थियों का आकार.
किसी कंपनी के कर्मचारियों का आईक्यू.
एक दिन में किसी कारखाने में उत्पादित दोषपूर्ण भागों की संख्या।
किसी पाठ्यक्रम में छात्रों द्वारा परीक्षा में प्राप्त ग्रेड।
स्टॉक एक्सचेंज में सूचीबद्ध कंपनियों के शेयरों की लाभप्रदता।

सामान्य वितरण ग्राफ

एक बार जब हमने देखा कि सामान्य वितरण क्या है और इस प्रकार के संभाव्यता वितरण के कुछ उदाहरण हैं, तो आइए देखें कि अवधारणा को बेहतर ढंग से समझने के लिए इसका ग्राफ कैसा दिखता है।

निम्नलिखित ग्राफ़ में, आप देख सकते हैं कि सामान्य वितरण का घनत्व कार्य उसके अंकगणितीय माध्य और मानक विचलन के मूल्यों के आधार पर कैसे भिन्न होता है।

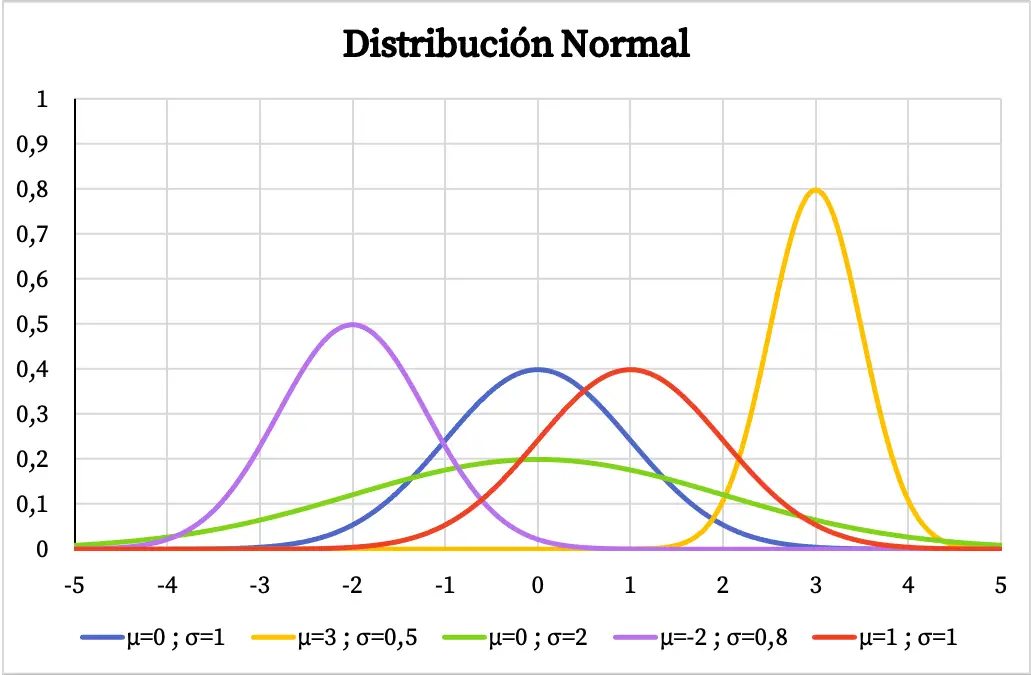
अंकगणितीय माध्य पर केंद्रित एक घंटी का आकार होने पर, यदि किसी चर का सामान्य वितरण होता है तो इसका मतलब है कि सबसे अधिक दोहराया गया मान माध्य है और माध्य के आसपास के मान चरम मानों की तुलना में अधिक बार दोहराए जाते हैं। इसी तरह, सामान्य वितरण का मानक विचलन जितना बड़ा होगा, उसके ग्राफिकल प्रतिनिधित्व का आकार उतना ही अधिक होगा।

दूसरी ओर, सामान्य वितरण के संचयी संभाव्यता फ़ंक्शन का ग्राफ़ इसके अंकगणितीय माध्य और मानक विचलन के मूल्यों पर भी निर्भर करता है, जैसा कि आप निम्नलिखित छवि में देख सकते हैं:

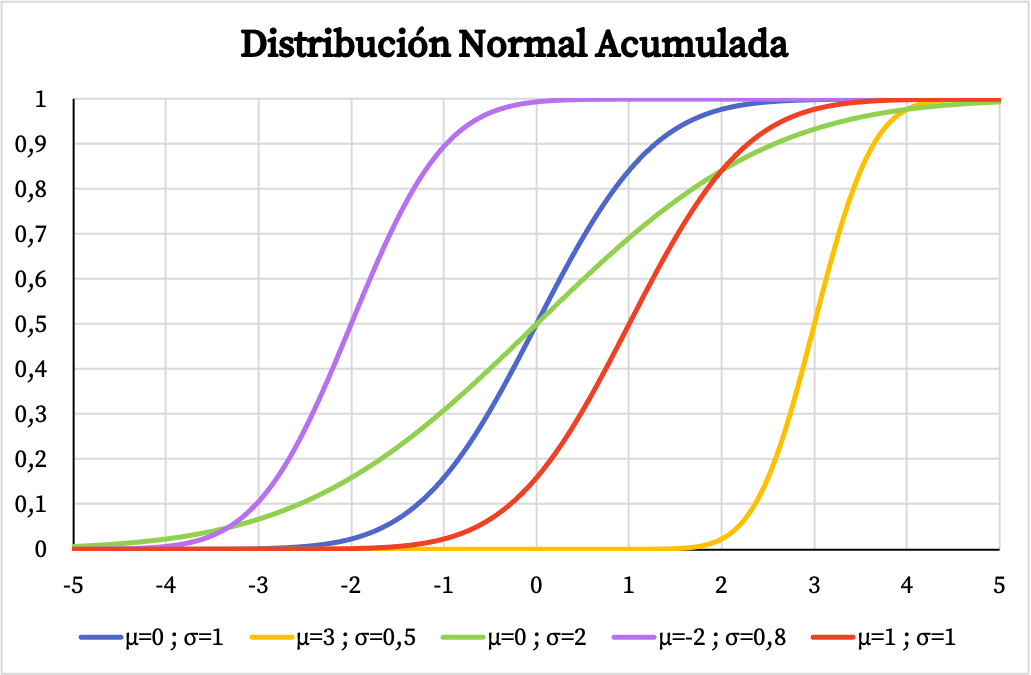
सामान्य वितरण का घनत्व फ़ंक्शन और वितरण फ़ंक्शन इस वितरण से जुड़ी संभावनाओं की गणना करना संभव बनाता है। हालाँकि, उनके सूत्रों का उपयोग करने के बजाय, आप सीधे सामान्य वितरण तालिकाओं का उपयोग कर सकते हैं क्योंकि यह तेज़ है। आप निम्नलिखित लिंक पर इन तालिकाओं से परामर्श ले सकते हैं:

➤ देखें: सामान्य वितरण तालिका

सामान्य वितरण के लक्षण

सामान्य वितरण में निम्नलिखित विशेषताएं हैं:

सामान्य वितरण दो विशिष्ट मापदंडों पर निर्भर करता है, जो इसका अंकगणितीय माध्य (μ) और इसका मानक विचलन (σ) हैं।

$X\sim N(\mu,\sigma)$

सामान्य वितरण सकारात्मक और नकारात्मक मान ले सकता है, इसलिए सामान्य वितरण के डोमेन में वास्तविक संख्याएँ होती हैं।

$x\in \mathbb{R}$

सामान्य वितरण का माध्यिका और मोड वितरण के अंकगणितीय माध्य के बराबर होते हैं।

$Me=Mo=\mu$

सामान्य वितरण का तिरछापन गुणांक और कर्टोसिस गुणांक शून्य हैं।

$\begin{array}{c}A=0\\[2ex]C=0\end{array}$

सामान्य वितरण के घनत्व फलन का सूत्र है:

$\displaystyle P[X=x]=\frac1{\sigma\sqrt{2\pi}}\; e^{ - \frac{(x-\mu)^2}{2\sigma^2}}$

इसी प्रकार, सामान्य वितरण के संचयी संभाव्यता फलन का सूत्र है:

$\displaystyle P[X\leq x]=\frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^x e^{-\frac{(x - \mu)^2}{2\sigma^2}}\, dx ,\quad x\in\mathbb{R}$

केंद्रीय सीमा प्रमेय का एक अनुप्रयोग यह है कि जब λ का मान पर्याप्त रूप से बड़ा हो तो एक पॉइसन वितरण एक सामान्य वितरण का अनुमान लगा सकता है।

$\text{Poisson}(\lambda)\ \color{orange}\bm{\longrightarrow}\color{black} \ N\left(\lambda, \sqrt{\lambda}\right)$

केंद्रीय सीमा प्रमेय का एक अन्य अनुप्रयोग यह है कि एक द्विपद वितरण को बड़ी संख्या में अवलोकनों के साथ डेटा सेट के लिए सामान्य वितरण द्वारा अनुमानित किया जा सकता है।

$\text{Bin}(n,p)\ \color{orange}\bm{\longrightarrow}\color{black} \ N\left(n\cdot p, \sqrt{n\cdot p \cdot (1-p)}\right)$

मानक सामान्य वितरण

मानक सामान्य वितरण , जिसे इकाई सामान्य वितरण भी कहा जाता है, सामान्य वितरण का सबसे सरल मामला है। अधिक सटीक रूप से, मानक सामान्य वितरण क्रमशः 0 और 1 के बराबर माध्य और मानक विचलन मान वाला एक सामान्य वितरण है।

$\displaystyle N(0,1) \ \color{orange}\bm{\longrightarrow}\color{black}\begin{cases} \mu=0\\[2ex]\sigma=1\end{cases}$

ध्यान दें कि टाइपिंग नामक प्रक्रिया को लागू करके किसी भी सामान्य वितरण को मानक सामान्य वितरण में बदला जा सकता है, जिसमें प्रत्येक मान से उसके अंकगणितीय माध्य को घटाना और फिर उसके मानक विचलन से विभाजित करना शामिल है।

इसके अतिरिक्त, मानक सामान्य वितरण का उपयोग इसकी संभाव्यता तालिका का उपयोग करके सामान्य वितरण की किसी भी संभावना को निर्धारित करने के लिए किया जाता है। इसलिए, सामान्य वितरण की संभावना खोजने के लिए, इसे मानक सामान्य वितरण में बदलने के लिए पहले चर दर्ज किया जाता है और फिर, हम तालिका में देखते हैं कि संबंधित संभावना मान क्या है। अधिक जानने के लिए निम्नलिखित लिंक पर क्लिक करें:

➤ देखें: मानक सामान्य वितरण

सामान्य वितरण और अनुभवजन्य नियम

आंकड़ों में, अंगूठे का नियम , जिसे 68-95-99.7 नियम भी कहा जाता है, एक नियम है जो सामान्य वितरण में मूल्यों के प्रतिशत को परिभाषित करता है जो माध्य के तीन मानक विचलन के भीतर आते हैं।

अधिक विशेष रूप से, अंगूठे का नियम निम्नलिखित बताता है:

सामान्य वितरण में 68% मान माध्य के एक मानक विचलन के भीतर होते हैं।
सामान्य वितरण में 95% मान माध्य के दो मानक विचलन के भीतर होते हैं।
सामान्य वितरण में 99.7% मान माध्य के तीन मानक विचलन के अंतर्गत आते हैं।

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने