लॉगनॉर्मल वितरण

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 3, 2023 संभावना शून्य टिप्पणियां

यह आलेख बताता है कि आंकड़ों में असामान्य वितरण क्या है। तो, आप पता लगाएंगे कि लॉगनॉर्मल वितरण के गुण क्या हैं और इस प्रकार के संभाव्यता वितरण का ग्राफ क्या है।

लॉगनॉर्मल वितरण क्या है?

लॉगनॉर्मल डिस्ट्रीब्यूशन , या लॉगनॉर्मल डिस्ट्रीब्यूशन , एक संभाव्यता वितरण है जो एक यादृच्छिक चर को परिभाषित करता है जिसका लघुगणक एक सामान्य वितरण का अनुसरण करता है।

इसलिए, यदि चर X का सामान्य वितरण है, तो घातीय फ़ंक्शन e ^x का लॉगनॉर्मल वितरण है।

$X\sim \text{Lognormal}(\mu,\sigma^2)$

ध्यान दें कि लॉगनॉर्मल वितरण का उपयोग केवल तभी किया जा सकता है जब चर मान सकारात्मक हों, क्योंकि लघुगणक एक ऐसा फ़ंक्शन है जो केवल एक सकारात्मक तर्क लेता है।

आंकड़ों में लॉगनॉर्मल वितरण के विभिन्न अनुप्रयोगों के बीच, हम वित्तीय निवेशों का विश्लेषण करने और विश्वसनीयता विश्लेषण करने के लिए इस वितरण के उपयोग को अलग करते हैं।

लॉगनॉर्मल डिस्ट्रीब्यूशन को टिनॉट डिस्ट्रीब्यूशन के रूप में भी जाना जाता है, कभी-कभी इसे लॉगनॉर्मल डिस्ट्रीब्यूशन या लॉग-नॉर्मल डिस्ट्रीब्यूशन के रूप में भी लिखा जाता है।

लॉगनॉर्मल वितरण का प्लॉट

अब जब हम लॉगनॉर्मल वितरण की परिभाषा जानते हैं, तो हम इस अनुभाग में देखेंगे कि लॉगनॉर्मल वितरण का ग्राफिकल प्रतिनिधित्व इसके अंकगणितीय माध्य और इसके मानक विचलन के मूल्यों के आधार पर कैसे भिन्न होता है।

लघुगणक वितरण के घनत्व फलन का ग्राफ इस प्रकार है:

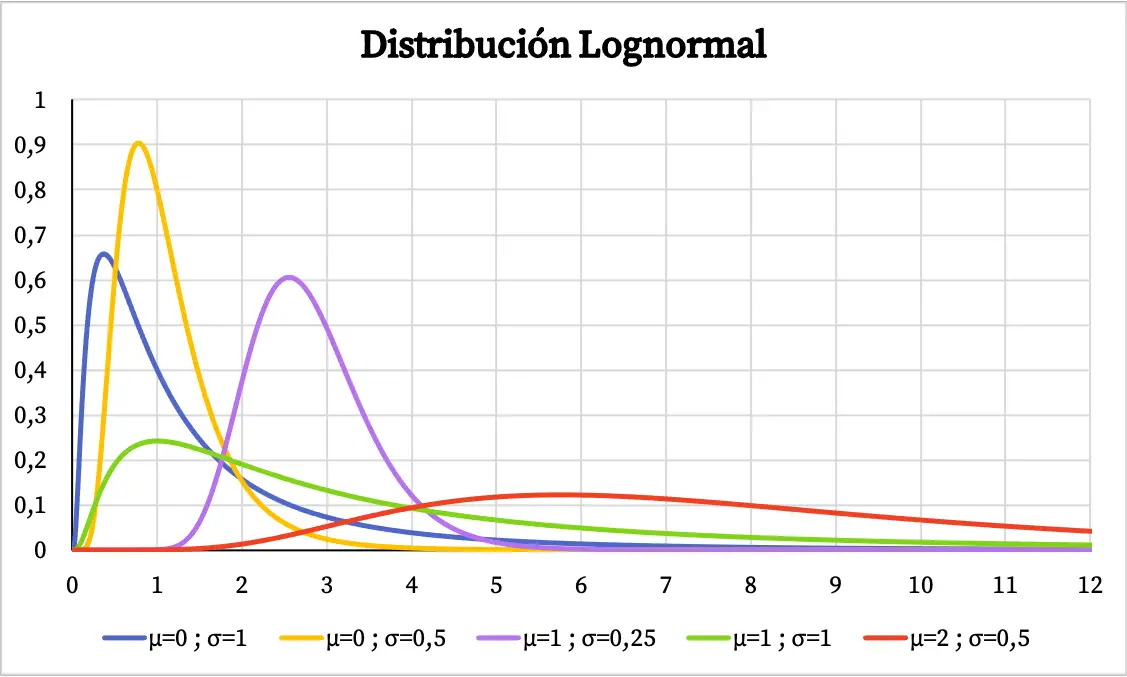
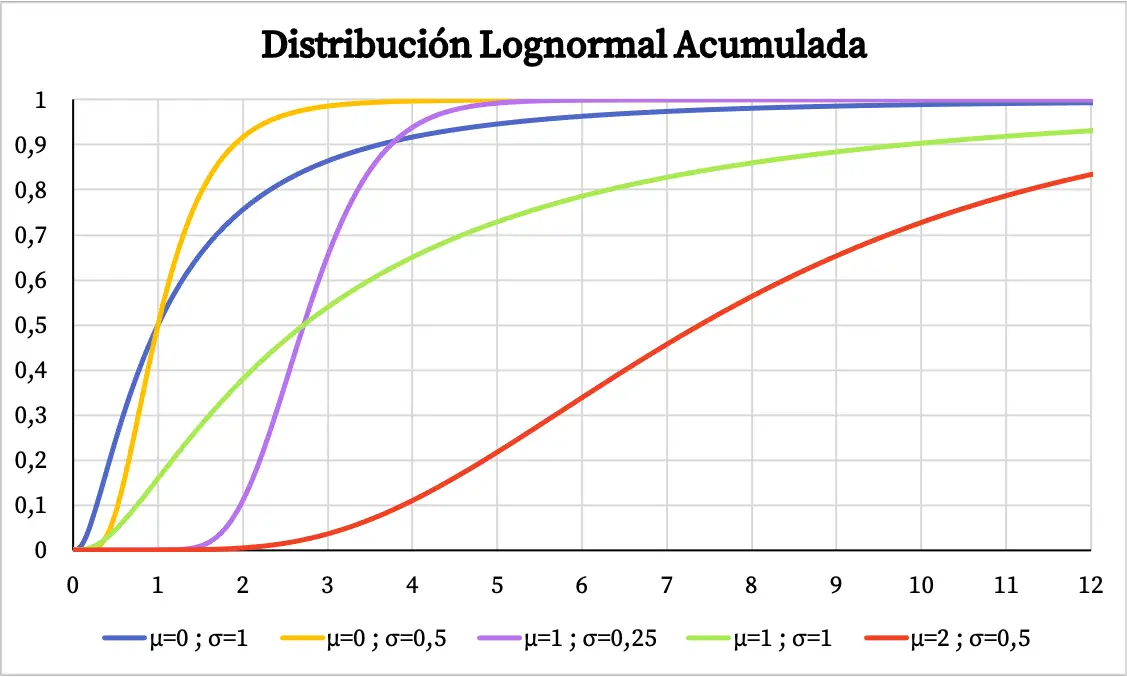
दूसरी ओर, लॉगनॉर्मल वितरण का संचयी संभाव्यता ग्राफ इस प्रकार है:

लॉगनॉर्मल वितरण का संचयी संभाव्यता प्लॉट

लघुगणक वितरण के लक्षण

लॉगनॉर्मल वितरण में निम्नलिखित विशेषताएं हैं:

लॉगनॉर्मल वितरण को दो मापदंडों के मान से परिभाषित किया गया है, इसका अंकगणितीय माध्य μ और इसका विचरण σ ² ।

$X\sim \text{Lognormal}(\mu,\sigma^2)$

लॉगनॉर्मल वितरण के डोमेन में सकारात्मक वास्तविक संख्याएँ होती हैं, क्योंकि लघुगणक नकारात्मक या शून्य मान स्वीकार नहीं करता है।

$x\in (0,+\infty)$

एक लॉगनॉर्मल वितरण की अपेक्षा माध्य और दो से विभाजित विचरण के योग तक बढ़ाई गई संख्या ई के बराबर है।

$\displaystyle E[X]=e^{\mu+\frac{\sigma^2}{2}}$

दूसरी ओर, एक लॉगनॉर्मल वितरण के विचरण की गणना निम्नलिखित अभिव्यक्ति से की जा सकती है:

$Var(X)=\left(e^{\sigma^2}-1\right)\cdot e^{2\mu+\sigma^2$

लॉगनॉर्मल वितरण का मोड वितरण के माध्य तक बढ़ाई गई संख्या ई के बराबर है।

$Mo=e^\mu$

लॉगनॉर्मल वितरण का विषमता गुणांक निम्नलिखित सूत्र को लागू करके निर्धारित किया जा सकता है:

$\displaystyle A=\left(e^{\sigma^2}+2\right)\cdot\sqrt{e^{\sigma^2}-1}$

लघुगणक वितरण के घनत्व फलन का सूत्र है:

$\displaystyle P[X=x]=\frac{1}{\sigma \cdot x\cdot \sqrt{2 \pi}}\cdot \exp\left(-\frac{(\ln x-\mu)^2}{2\sigma^2}\right)$

लॉगनॉर्मल वितरण के संचयी संभाव्यता फ़ंक्शन का सूत्र है:

$\displaystyle P[X\leq x]=\Phi\left(\frac{\ln x-\mu}{\sigma}\right)$

सोना

$\Phi$

मानक सामान्य वितरण का संचयी संभाव्यता फलन है।

एक लघुगणकीय वितरण का अंकगणितीय माध्य उसके माध्यिका के मान से अधिक होता है।

$\mu > Me” title=”Rendered by QuickLaTeX.com” height=”16″ width=”61″ style=”vertical-align: -4px;”></p></p> </div>  <div class=$

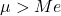
लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने

लॉगनॉर्मल वितरण क्या है?

लॉगनॉर्मल वितरण का प्लॉट

लघुगणक वितरण के लक्षण

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

एक टिप्पणी जोड़ने