पाइ चार्ट

यह लेख बताता है कि पाई चार्ट क्या हैं, पाई चार्ट कैसे बनाया जाता है और इसके अलावा, आप इस प्रकार के सांख्यिकीय ग्राफ का चरण-दर-चरण अभ्यास देख पाएंगे।

पाई चार्ट क्या है?

पाई चार्ट , या पाई चार्ट , एक प्रकार का सांख्यिकीय आरेख है जिसमें डेटा को सेक्टरों में विभाजित एक सर्कल द्वारा दर्शाया जाता है, जैसे कि प्रत्येक सेक्टर का कोण उसकी संबंधित आवृत्ति के समानुपाती होता है।

दूसरे शब्दों में, किसी मान की आवृत्ति जितनी अधिक होगी, आरेख में उसका संगत क्षेत्र उतना ही बड़ा होगा।

इसलिए, प्रत्येक मान की आवृत्ति का दृश्य विश्लेषण करने के लिए पाई चार्ट का उपयोग किया जाता है। सांख्यिकी में, इस प्रकार के ग्राफ़ का उपयोग मुख्य रूप से गुणात्मक चर को दर्शाने के लिए किया जाता है।

पाई चार्ट कैसे बनाये

पाई चार्ट बनाने के चरण इस प्रकार हैं:

1. जिस नमूने का आप विश्लेषण करना चाहते हैं उससे सांख्यिकीय डेटा एकत्र करें और आवृत्ति तालिका बनाएं।
2. आरेख के प्रत्येक त्रिज्यखंड के कोण की गणना करें। ऐसा करने के लिए, आपको निम्न सूत्र का उपयोग करना होगा:



सोना



सेक्टर I का कोण है,



इसकी पूर्ण आवृत्ति और



डेटा की कुल संख्या.

3. परिकलित कोणों से, एक कोण चांदे का उपयोग करके एक वृत्ताकार ग्राफ़ में क्षेत्रों का प्रतिनिधित्व करें।
4. निम्नलिखित सूत्र का उपयोग करके चार्ट में प्रत्येक सेक्टर के प्रतिशत की गणना करें:



सोना



सेक्टर I का प्रतिशत है,



इसकी पूर्ण आवृत्ति और



डेटा की कुल संख्या.

5. आरेख में प्रत्येक सेक्टर का प्रतिशत इंगित करें।

पाई चार्ट उदाहरण

तो आप देख सकते हैं कि पाई चार्ट कैसे बनाया जाता है, नीचे चरण-दर-चरण उदाहरण दिया गया है:

• 50 लोगों से उनके पसंदीदा शहर के बारे में पूछा गया और डेटा को निम्नलिखित तालिका में संकलित किया गया। इस सांख्यिकीय डेटा को पाई चार्ट में प्रस्तुत करें।

सबसे पहले, हमें प्रत्येक सेक्टर से संबंधित कोण की गणना करनी चाहिए, इसलिए हम प्रत्येक मान के लिए निम्नलिखित सूत्र का उपयोग करते हैं:

उदाहरण के लिए, पहले मान से संबंधित सेक्टर के कोण की गणना करना है:

और फिर हम कोण चांदा का उपयोग करके गणना किए गए कोण के अनुरूप क्षेत्र को एक वृत्त में खींचते हैं:

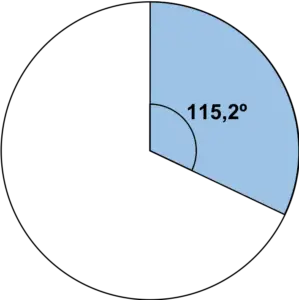
हम सभी मानों के लिए समान प्रक्रिया दोहराते हैं:

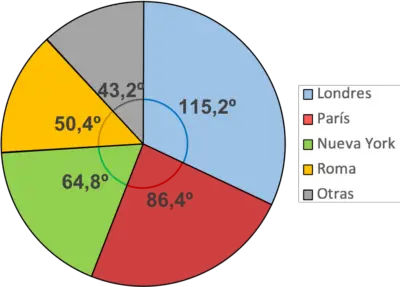
प्रत्येक सेक्टर को अलग-अलग रंग में रंगने की अनुशंसा की जाती है, ताकि उन्हें अलग करना आसान हो सके। इसी तरह, प्रत्येक रंग का अर्थ बताने के लिए एक किंवदंती जोड़ी जानी चाहिए।

एक बार सभी क्षेत्रों का प्रतिनिधित्व हो जाने पर, प्रत्येक से संबंधित प्रतिशत की गणना करना आवश्यक है। ऐसा करने के लिए, हम निम्नलिखित सूत्र लागू करते हैं:

इसलिए प्रत्येक क्षेत्र का प्रतिशत है:

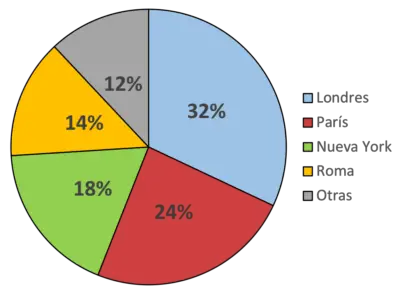
इस आरेख के साथ हम इंगित करते हैं कि, उदाहरण के लिए, नीला रंग लंदन शहर का प्रतिनिधित्व करता है, जो वह शहर है जिसे अधिकांश लोग (32% लोग) पसंद करते हैं। इसी तरह, हरा रंग न्यूयॉर्क का प्रतिनिधित्व करता है, जो 18% उत्तरदाताओं का पसंदीदा शहर है।

पाई चार्ट के फायदे और नुकसान

अपनी विशेषताओं के कारण, पाई चार्ट के निम्नलिखित फायदे और नुकसान हैं:

फ़ायदा:

• यह एक बहुत ही दृश्य सांख्यिकीय ग्राफ है, जो आपको शीघ्रता से विश्लेषण करने और निष्कर्ष निकालने की अनुमति देता है।
• यह गुणात्मक डेटा को ग्राफ़ करने के लिए बहुत उपयोगी है।
• यदि यह कंप्यूटर के साथ किया जाता है, उदाहरण के लिए एक्सेल के साथ, तो यह बहुत जल्दी हो जाता है।

नुकसान:

• जब चार्ट पर कई अलग-अलग सेक्टर हों, तो चार्ट को पढ़ना जटिल हो सकता है। इस मामले में, छोटे क्षेत्रों को “अन्य” नामक एक एकल क्षेत्र में समूहित करने की अनुशंसा की जाती है।
• अन्य प्रकार के सांख्यिकीय आरेख हैं जो मात्रात्मक चर या समय श्रृंखला का प्रतिनिधित्व करने के लिए अधिक उपयुक्त हैं।