स्कैटर प्लॉट

यह आलेख बताता है कि स्कैटर प्लॉट क्या हैं। इसलिए आप जानेंगे कि बिंदु बादल का उपयोग किस लिए किया जाता है, बिंदु बादल कैसे बनाया जाता है, इसकी व्याख्या कैसे की जाती है और बिंदु बादल के उदाहरण।

बिंदु बादल क्या है?

स्कैटरप्लॉट , या स्कैटरप्लॉट , एक प्रकार का सांख्यिकीय आरेख है जिसमें दो चर का एक डेटा सेट दो कार्टेशियन समन्वय अक्षों पर रेखांकन किया जाता है।

इसलिए, दो सांख्यिकीय चरों के बीच संबंधों का विश्लेषण करने के लिए स्कैटर प्लॉट का उपयोग किया जाता है।

स्कैटरप्लॉट के कई अलग-अलग नाम हैं, जैसे सहसंबंध आरेख या स्कैटरप्लॉट ।

यह ध्यान दिया जाना चाहिए कि स्कैटर आरेख को पेरेटो चार्ट, कारण और प्रभाव आरेख, फ़्लोचार्ट इत्यादि की तरह, गुणवत्ता नियंत्रण के बुनियादी उपकरणों में से एक माना जाता है।

स्कैटर प्लॉट कैसे बनाएं

स्कैटर प्लॉट बनाने के लिए, आपको निम्नलिखित चरणों का पालन करना होगा:

1. जिस नमूने का आप विश्लेषण करना चाहते हैं, उससे सांख्यिकीय डेटा एकत्र करें। ध्यान रखें कि स्कैटर प्लॉट बनाने के लिए कम से कम दो मात्रात्मक चर होने चाहिए।
2. स्कैटर प्लॉट के दो अक्षों को प्लॉट करें।
3. दो सांख्यिकीय चर निर्धारित करें जिनका रेखांकन किया जाएगा।
4. ग्राफ़ के प्रत्येक अक्ष के पैमाने को कैलिब्रेट करें। ऐसा करने के लिए, पहले प्रत्येक चर का न्यूनतम और अधिकतम पता लगाने और, इन मानों के आधार पर, प्रत्येक अक्ष को स्केल करने की अनुशंसा की जाती है।
5. स्कैटरप्लॉट पर डेटा के प्रत्येक जोड़े को एक बिंदु के साथ निरूपित करें।
6. प्राप्त प्रकीर्ण आरेख का विश्लेषण एवं व्याख्या करें।

स्कैटरप्लॉट उदाहरण

स्कैटर आरेख की परिभाषा और इसके निर्माण के सिद्धांत को देखने के बाद, यह खंड एक उदाहरण के रूप में इस प्रकार के आरेख का प्रतिनिधित्व करता है।

• निम्नलिखित आवृत्ति तालिका में, 20 छात्रों के नमूने के गणित और सांख्यिकी अंक डेटा के रूप में एकत्र किए गए थे। डेटासेट को स्कैटरप्लॉट पर प्लॉट करें और उसका विश्लेषण करें।

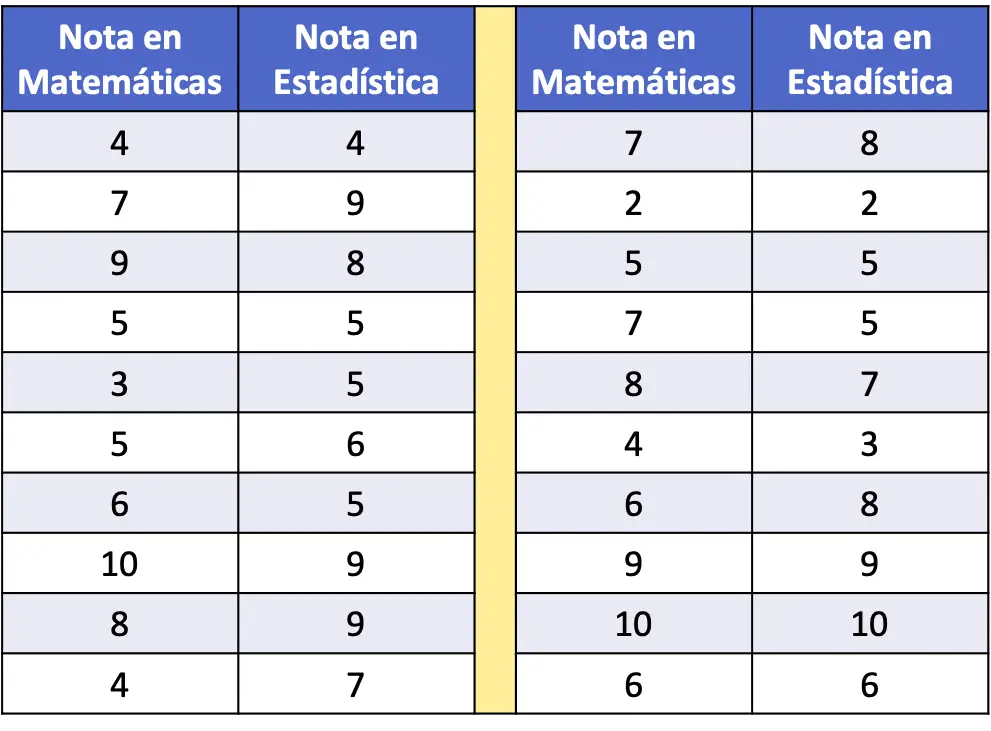
स्कैटर प्लॉट में डेटा श्रृंखला का प्रतिनिधित्व करने के लिए, हमें बस दो अक्षों को प्लॉट करना होगा, उन्हें कैलिब्रेट करना होगा, और डेटा की प्रत्येक जोड़ी के लिए ग्राफ़ पर एक बिंदु प्लॉट करना होगा। याद रखें कि ग्राफ़ पर एक बिंदु उसके प्रत्येक मान के अनुरूप काल्पनिक रेखाओं के प्रतिच्छेदन पर रखा गया है।

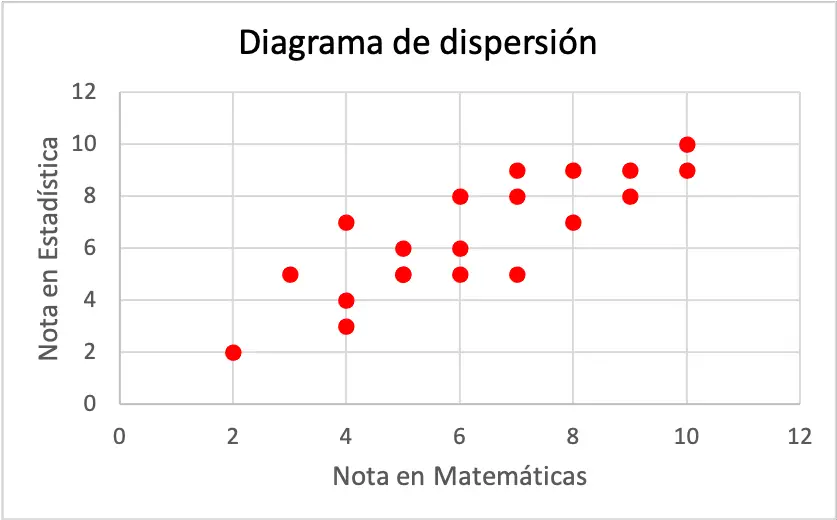
स्कैटर प्लॉट का प्रत्येक अक्ष एक चर का प्रतिनिधित्व करता है। अधिक सटीक रूप से, क्षैतिज अक्ष गणित में प्राप्त ग्रेड से संबंधित है और दूसरी ओर, ऊर्ध्वाधर अक्ष सांख्यिकी में प्राप्त ग्रेड से मेल खाता है।

जैसा कि आप स्कैटरप्लॉट से देख सकते हैं, दोनों चरों में सकारात्मक सहसंबंध है, क्योंकि एक चर बढ़ता है तो दूसरा चर भी बढ़ता है। इसलिए, यह निष्कर्ष निकाला गया है कि यदि किसी छात्र को गणित में बेहतर ग्रेड मिलता है, तो यह अधिक संभावना है कि उसे सांख्यिकी में भी बेहतर ग्रेड मिलेगा, और इसके विपरीत।

हालाँकि, पिछले निष्कर्ष का मतलब यह नहीं है कि एक चर दूसरे का कारण है, क्योंकि गणित में अच्छा ग्रेड प्राप्त करना स्वचालित रूप से कुछ भी किए बिना सांख्यिकी में अच्छे ग्रेड की गारंटी नहीं देता है, बल्कि व्यक्ति को दोनों विषयों का अध्ययन करना चाहिए। अगले भाग में, हम इस अवधारणा के बारे में अधिक विस्तार से जानेंगे।

बिखराव की साजिश और सहसंबंध

स्कैटर आरेख से, दो चरों के बीच सहसंबंध के प्रकार की पहचान करना संभव है:

• प्रत्यक्ष सहसंबंध (या सकारात्मक सहसंबंध) : एक चर तब बढ़ता है जब दूसरा भी बढ़ता है।
• व्युत्क्रम सहसंबंध (या नकारात्मक सहसंबंध) : जब एक चर बढ़ता है, तो दूसरा घटता है, और इसके विपरीत, यदि एक चर घटता है, तो दूसरा बढ़ता है।
• शून्य सहसंबंध (कोई सहसंबंध नहीं) : दो चर के बीच कोई संबंध नहीं है।

इसी प्रकार, चाहे दो चर के बीच सहसंबंध प्रत्यक्ष या उलटा हो, सहसंबंध को दो चर के बीच संबंध की ताकत या कमजोरी के आधार पर भी वर्गीकृत किया जा सकता है।

• मजबूत सहसंबंध: दो चर बारीकी से जुड़े हुए हैं। बिंदुओं को बिंदु बादल पर एक साथ लाया जाता है। इससे चरों के बीच संबंध की पहचान करना आसान हो जाता है।
• कम सहसंबंध : दो चरों के बीच एक संबंध मौजूद है, लेकिन इसे पहचानना मुश्किल है। बिंदु बादल पर बिंदु एक दूसरे से बहुत दूर हैं।

दूसरी ओर, सहसंबंध की गणना एक सूत्र का उपयोग करके संख्यात्मक रूप से भी की जा सकती है, जिससे आप गणितीय रूप से जान सकते हैं कि दो अलग-अलग चर कितने निकट से संबंधित हैं। यह कैसे काम करता है यह देखने के लिए निम्नलिखित लिंक पर क्लिक करें:

ध्यान रखें कि यदि दो चरों के बीच सहसंबंध है, तो भी इसका मतलब यह नहीं है कि उनके बीच कार्य-कारण है, अर्थात दो चरों के बीच संबंध का मतलब यह नहीं है कि एक चर में परिवर्तन दूसरे में परिवर्तन का कारण है। चर।

तो, पिछले अनुभाग में स्कैटरप्लॉट की तरह, हालांकि गणित ग्रेड और सांख्यिकी ग्रेड के बीच एक सकारात्मक संबंध है, गणित में अच्छा ग्रेड प्राप्त करने का मतलब सांख्यिकी में अच्छा ग्रेड प्राप्त करना नहीं है, क्योंकि यदि आप केवल गणित का अध्ययन करते हैं, तो आप निश्चित रूप से असफल होंगे सांख्यिकी में. इसलिए, दोनों चर संबंधित हैं लेकिन वे कारण और प्रभाव नहीं हैं।

अधिक जानने के लिए, आप निम्नलिखित पोस्ट जारी रख सकते हैं:

पॉइंट क्लाउड के फायदे और नुकसान

स्कैटरप्लॉट की विशेषताओं के कारण, इस प्रकार के सांख्यिकीय चार्ट के फायदे और नुकसान हैं।

फ़ायदा:

• स्कैटर प्लॉट पर डेटा की एक श्रृंखला का प्रतिनिधित्व करना काफी सरल है।
• स्कैटरप्लॉट आपको दो चरों के बीच संबंधों का दृश्य रूप से विश्लेषण करने की अनुमति देता है, जिससे निष्कर्ष निकालना आसान हो जाता है।
• स्कैटरप्लॉट का उपयोग गहन सांख्यिकीय अध्ययन में प्रारंभिक डेटा अन्वेषण के रूप में भी किया जा सकता है।

नुकसान:

• इस प्रकार के चित्र गुणात्मक चरों को दर्शाने के लिए उपयोगी नहीं होते हैं।
• स्कैटर प्लॉट की व्याख्या करने से दो चरों के बीच कारण और प्रभाव का गलत निष्कर्ष निकल सकता है।
• स्कैटरप्लॉट आपको दो से अधिक चरों के बीच संबंधों का विश्लेषण करने की अनुमति नहीं देते हैं।