हाइपरज्यामितीय वितरण

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 6, 2023 संभावना शून्य टिप्पणियां

इस लेख में हम बताते हैं कि हाइपरज्यामितीय वितरण क्या है और इस प्रकार के वितरण के साथ संभाव्यता की गणना कैसे की जाती है। आपको ऑनलाइन हाइपरजियोमेट्रिक वितरण का सूत्र मिलेगा, इसकी विशेषताएं क्या हैं, साथ ही हाइपरजियोमेट्रिक वितरण की संभावना की गणना करने के लिए एक कैलकुलेटर भी मिलेगा।

हाइपरज्यामितीय वितरण क्या है?

हाइपरजियोमेट्रिक वितरण एक संभाव्यता वितरण है जो किसी जनसंख्या से n तत्वों के प्रतिस्थापन के बिना यादृच्छिक निष्कर्षण में सफल मामलों की संख्या का वर्णन करता है।

अर्थात्, किसी जनसंख्या से n तत्वों को बिना किसी प्रतिस्थापन के निकालते समय x सफलताएँ प्राप्त करने की संभावना की गणना करने के लिए हाइपरजियोमेट्रिक वितरण का उपयोग किया जाता है।

हाइपरजियोमेट्रिक वितरण के तीन पैरामीटर हैं:

एन : जनसंख्या में तत्वों की संख्या है (एन = 0, 1, 2,…)।
K : सफलता के मामलों की अधिकतम संख्या है (K = 0, 1, 2,…,N)। चूंकि हाइपरजियोमेट्रिक वितरण में किसी तत्व को केवल “सफलता” या “विफलता” माना जा सकता है, एनके विफलता के मामलों की अधिकतम संख्या है।
n : किए गए बिना-प्रतिस्थापन फ़ेच की संख्या है।

$X \sim HG(N,K,n)$

उदाहरण के लिए, एक असतत यादृच्छिक चर

$X \sim HG(8,5,3)$

हाइपरज्यामितीय वितरण सूत्र

हाइपरज्यामितीय वितरण का सूत्र x पर K की संयोजन संख्या का गुणनफल है जिसे nx पर NK की संयोजन संख्या से n पर N की संयोजन संख्या से विभाजित किया जाता है।

जहां N जनसंख्या का आकार है, K अनुकूल मामलों की कुल संख्या है, n प्रतिस्थापन के बिना निष्कर्षणों की संख्या है और x अनुकूल मामलों की संख्या है जिसके लिए घटना की संभावना की गणना की जानी चाहिए।

👉 आप हाइपरज्यामितीय वितरण का अनुसरण करने वाले एक चर की घटना की संभावना की गणना करने के लिए नीचे दिए गए कैलकुलेटर का उपयोग कर सकते हैं।

हाइपरज्यामितीय वितरण का उदाहरण

एक बार जब हमने हाइपरजियोमेट्रिक वितरण की परिभाषा और सूत्र देख लिया है, तो अब हम चरण दर चरण एक उदाहरण को हल करेंगे ताकि आप जान सकें कि हाइपरज्यामितीय वितरण की संभावना की गणना कैसे करें।

एक बैग में हमने 20 नीली गेंदें और 30 लाल गेंदें रखीं, यानी बैग के अंदर कुल मिलाकर 50 गेंदें हैं। यदि हम बिना किसी प्रतिस्थापन के 12 गेंदें निकालते हैं, तो 4 नीली गेंदें निकलने की प्रायिकता ज्ञात कीजिए।

अभ्यास को हल करने के लिए सबसे पहली चीज़ जो हमें करने की ज़रूरत है वह है हाइपरज्यामितीय वितरण के मापदंडों की पहचान करना। इस मामले में, जनसंख्या में तत्वों की कुल संख्या 50 ( एन =50) है, अनुकूल मामलों की अधिकतम संख्या 20 ( के =20) है, और 12 गेंदें निकाली गई हैं ( एन =12)।

$\left.\begin{array}{c}N=50\\[2ex]K=20\\[2ex]n=12\end{array}\right\} \longrightarrow \ X\sim HG(50,20,12)$

हम 4 नीली गेंदें ( x =4) निकालने की संभावना की गणना करना चाहते हैं, इसलिए हम हाइपरज्यामितीय वितरण सूत्र लागू करते हैं, चर को उनके संबंधित मानों से प्रतिस्थापित करते हैं और गणना करते हैं:

$P\bigl[X=x\bigr]=\cfrac{\begin{pmatrix}K\\x\end{pmatrix}\begin{pmatrix}N-K\\n-x\end{pmatrix}}{\begin{pmatrix}N\\n\end{pmatrix}}$

$\begin{aligned}P\bigl[X=4\bigr]&=\cfrac{\begin{pmatrix}20\\4\end{pmatrix}\begin{pmatrix}50-20\\12-4\end{pmatrix}}{\begin{pmatrix}50\\12\end{pmatrix}} \\[1.5ex]&=\cfrac{\begin{pmatrix}20\\4\end{pmatrix}\begin{pmatrix}30\\8\end{pmatrix}}{\begin{pmatrix}50\\12\end{pmatrix}} \\[1.5ex]&=0,2336 \end{aligned}$

हाइपरज्यामितीय वितरण कैलकुलेटर

वांछित घटना के घटित होने की संभावना की गणना करने के लिए निम्नलिखित ऑनलाइन कैलकुलेटर में हाइपरजियोमेट्रिक वितरण के पैरामीटर दर्ज करें।

याद रखें कि N जनसंख्या का आकार है, K अनुकूल मामलों की कुल संख्या है, n नमूना आकार है और x वह मान है जिसके लिए हम ऐसा होने की संभावना ज्ञात करना चाहते हैं।

हाइपरज्यामितीय वितरण के लक्षण

हाइपरज्यामितीय वितरण में निम्नलिखित गुण हैं:

हाइपरज्यामितीय वितरण का अपेक्षित मूल्य नमूने में तत्वों की संख्या को अनुकूल मामलों की कुल संख्या से गुणा करके जनसंख्या में तत्वों की संख्या से विभाजित करने के बराबर है।

$E[X]=\cfrac{n\cdot K}{N}$

हाइपरज्यामितीय वितरण का तरीका n+1 के गुणनफल को K+1 से विभाजित करके N+2 से पूर्णांकित किया गया मान है।

$\displaystyle M=\Bigg\lfloor \frac{(n+1)(K+1)}{N+2}\Bigg\rfloor$

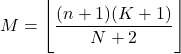
हाइपरज्यामितीय वितरण का विचरण निम्नलिखित अभिव्यक्ति का उपयोग करके प्राप्त किया जा सकता है:

$\displaystyle Var[X]=\cfrac{nK}{N}\left(\frac{N-K}{N}\right)\left(\frac{N-n}{N-1}\right)$

हाइपरज्यामितीय वितरण का क्षण उत्पन्न करने वाला कार्य इस प्रकार है:

$\cfrac{{N-K \choose n} \scriptstyle{\,_2F_1(-n, -K; N - K-n+1; e^{t}) } }{{N \choose n}}$

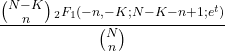
हाइपरजियोमेट्रिक वितरण का विशिष्ट कार्य इस प्रकार है:

$\cfrac{{N-K \choose n} \scriptstyle{\,_2F_1(-n, -K; N - K - n + 1; e^{it}) }}{{N \choose n}}$

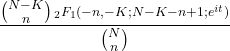
किसी दी गई संख्या में घटनाओं के घटित होने की संभावना की गणना हाइपरजियोमेट्रिक वितरण के लिए पुनरावर्ती का उपयोग करके पिछली संख्या की संभावना से की जा सकती है:

$P[X=x+1]=\cfrac{(K-x)(n-x)}{(x+1)(N-K-n+x-1)}\cdot P[X=x]$

हाइपरजियोमेट्रिक वितरण और द्विपद वितरण

हाइपरज्यामितीय वितरण और द्विपद वितरण के बीच का अंतर प्रतिस्थापन है। हाइपरजियोमेट्रिक वितरण का उपयोग तब किया जाता है जब पुनर्प्राप्ति को प्रतिस्थापित नहीं किया जाता है, हालांकि, द्विपद वितरण में पुनर्प्राप्ति को प्रतिस्थापित किया जाता है।

उदाहरण के लिए, यदि हम एक डेक में यादृच्छिक रूप से पांच कार्ड निकालते हैं और हम एक निश्चित कार्ड प्राप्त करने की संभावना की गणना करना चाहते हैं, यदि हम अपने द्वारा निकाले गए प्रत्येक कार्ड को प्रतिस्थापित नहीं करते हैं, तो हमें गणना करने के लिए हाइपरजियोमेट्रिक वितरण का उपयोग करना होगा। लेकिन यदि कार्ड निकालते समय हम उसे अगला निष्कर्षण करने से पहले वापस रख देते हैं, तो हमें संभाव्यता की गणना करने के लिए द्विपद वितरण का उपयोग करना चाहिए।

जब संख्या N बड़ी हो, अनुपात n/N छोटा हो और वांछित अनुकूल मामलों की संख्या बहुत छोटी हो, तो हम द्विपद वितरण के सन्निकटन के रूप में हाइपरजियोमेट्रिक वितरण का उपयोग कर सकते हैं। हालाँकि, मैं इसकी अनुशंसा नहीं करता क्योंकि परिणाम उतना विश्वसनीय नहीं होगा और इसके अलावा, हाइपरजियोमेट्रिक कानून की तुलना में द्विपद कानून के साथ संभावनाओं की गणना करना आसान है।

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने