अंकगणित औसत

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 6, 2023 आंकड़े शून्य टिप्पणियां

यहां हम बताते हैं कि अंकगणितीय माध्य क्या है और इसकी गणना कैसे की जाती है। आपको किसी भी सांख्यिकीय नमूने का अंकगणितीय माध्य खोजने के लिए अंकगणितीय माध्य उदाहरण और यहां तक कि एक कैलकुलेटर भी मिलेगा। अंत में, आप देख पाएंगे कि इस प्रकार के औसत के गुण क्या हैं और अंतरालों में समूहीकृत डेटा के साथ अंकगणितीय औसत कैसे प्राप्त किया जाता है।

अंकगणितीय माध्य क्या है?

अंकगणितीय माध्य सांख्यिकीय डेटा के एक सेट की एक केंद्रीय मूल्य विशेषता है। अंकगणितीय माध्य की गणना करने के लिए, सभी मानों को जोड़ा जाता है और डेटा की कुल संख्या से विभाजित किया जाता है।

इसके अलावा, अंकगणित माध्य किसी नमूने का सांख्यिकीय अध्ययन करने के लिए उपयोग किए जाने वाले मुख्य संकेतकों में से एक है।

इसलिए अंकगणितीय औसत का सूत्र इस प्रकार है:

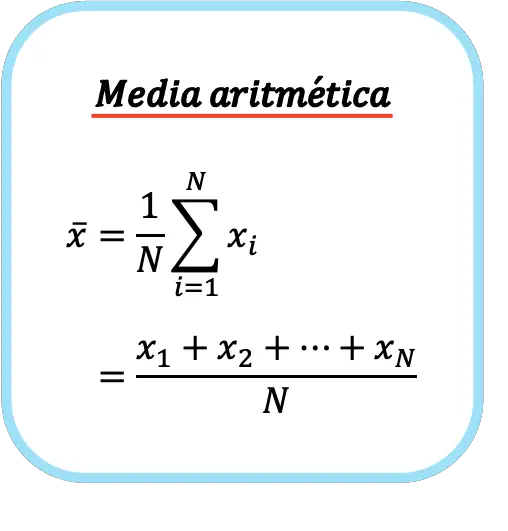
अंकगणितीय माध्य का प्रतीक अक्षर x के ऊपर एक क्षैतिज बैंड है।

$(\overline{x}).$

आप माध्य प्रतीक के साथ नमूना माध्य को जनसंख्या माध्य से अलग भी कर सकते हैं: एक नमूने का माध्य प्रतीक के साथ व्यक्त किया जाता है

$\overline{x}$

दूसरी ओर, जनसंख्या के औसत के लिए, हम ग्रीक अक्षर का उपयोग करते हैं

$\mu.$

यह ध्यान दिया जाना चाहिए कि किसी जनसंख्या का अंकगणितीय माध्य सांख्यिकीय चर के अपेक्षित मूल्य के बराबर है।

अंकगणितीय माध्य, जिसे अंकगणितीय माध्य भी कहा जाता है, एकमात्र प्रकार का माध्य नहीं है जो मौजूद है, इसमें भारित माध्य, वर्ग माध्य, ज्यामितीय माध्य और हार्मोनिक माध्य भी शामिल है। आप देख सकते हैं कि हमारी वेबसाइट के खोज इंजन में उनमें से प्रत्येक की गणना कैसे की जाती है।

अंकगणितीय माध्य की गणना कैसे करें

अंकगणितीय माध्य की गणना करने के लिए, निम्नलिखित चरणों का पालन किया जाना चाहिए:

नमूने से सभी सांख्यिकीय डेटा जोड़ें.
पिछले योग को डेटा की कुल संख्या से विभाजित करें।
प्राप्त परिणाम सांख्यिकीय नमूने का अंकगणितीय माध्य है।

👉 आप किसी भी डेटा सेट के अंकगणितीय माध्य की गणना करने के लिए नीचे दिए गए कैलकुलेटर का उपयोग कर सकते हैं।

अंकगणित माध्य की गणना का उदाहरण

अंकगणितीय माध्य की परिभाषा को देखते हुए, हम देखेंगे कि चरण दर चरण एक उदाहरण को हल करके डेटा के एक सेट का अंकगणितीय माध्य कैसे प्राप्त किया जाए।

एक छात्र ने स्कूल वर्ष के दौरान निम्नलिखित ग्रेड हासिल किए: गणित में 9, भाषा में 7, इतिहास में 6, अर्थशास्त्र में 8 और विज्ञान में 7.5। आपके सभी ग्रेडों का अंकगणितीय औसत क्या है?

अंकगणितीय औसत ज्ञात करने के लिए, हमें सभी ग्रेडों को जोड़ना होगा और फिर पाठ्यक्रम में विषयों की कुल संख्या से विभाजित करना होगा, जो कि 5 है। इसलिए, हम अंकगणितीय औसत सूत्र लागू करते हैं:

$\displaystyle\overline{x}=\frac{1}{N}\sum_{i=1}^N x_i=\frac{x_1+x_2+x_3+x_4+x_5}{N}$

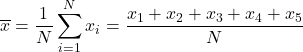
हम डेटा को सूत्र में प्रतिस्थापित करते हैं और अंकगणितीय औसत की गणना करते हैं:

$\overline{x}=\cfrac{9+7+5+8+7,5}{5}=7,3$

जैसा कि आप देख सकते हैं, अंकगणितीय औसत में, प्रत्येक मान को समान भार दिया जाता है, अर्थात, डेटा के प्रत्येक टुकड़े का संपूर्ण भार समान होता है।

अंकगणितीय औसत कैलकुलेटर

इसके अंकगणितीय माध्य की गणना करने के लिए किसी भी सांख्यिकीय नमूने से डेटा को निम्नलिखित कैलकुलेटर में दर्ज करें। डेटा को एक स्थान से अलग किया जाना चाहिए और दशमलव विभाजक के रूप में अवधि का उपयोग करके दर्ज किया जाना चाहिए।

समूहीकृत डेटा के लिए अंकगणितीय माध्य

समूहीकृत डेटा से हमारा तात्पर्य यह है कि डेटा को समूहों या अंतरालों के रूप में संरचित किया गया है। यह आमतौर पर तब होता है जब सांख्यिकीय नमूने का आकार बहुत बड़ा होता है।

इसलिए जब डेटा को एक साथ समूहीकृत किया जाता है तो अंकगणितीय माध्य की गणना थोड़ी भिन्न होती है, भले ही अवधारणा समान हो।

अंतरालों में समूहीकृत डेटा के अंकगणितीय माध्य की गणना करने के लिए, प्रत्येक समूह के वर्ग स्कोर को उसकी पूर्ण आवृत्ति से गुणा किया जाना चाहिए और फिर सभी पूर्ण आवृत्तियों के योग से विभाजित किया जाना चाहिए।

$\displaystyle\overline{x}=\frac{\sum_{i=1}^N x_i\cdot f_i}{\sum_{i=1}^N f_i} =\frac{x_1\cdot f_1+ x_2\cdot f_2+\dots +x_N\cdot f_N}{N}$

नोट: किसी अंतराल के वर्ग स्कोर की गणना अंतराल के अंतिम बिंदुओं के योग को दो से विभाजित करके की जाती है। उदाहरण के लिए, अंतराल [3,7) का वर्ग नोट होगा:

$\cfrac{3+7}{2}=5$

ताकि आप देख सकें कि यह कैसे किया जाता है, नीचे अंतरालों में समूहीकृत डेटा के अंकगणितीय माध्य पर एक हल किया गया अभ्यास दिया गया है:

हम एक समूह के वजन का सांख्यिकीय रूप से अध्ययन करना चाहते हैं, इसके लिए हमने 81 लोगों के एक प्रतिनिधि समूह का साक्षात्कार लिया और हमें निम्नलिखित डेटा प्राप्त हुआ:

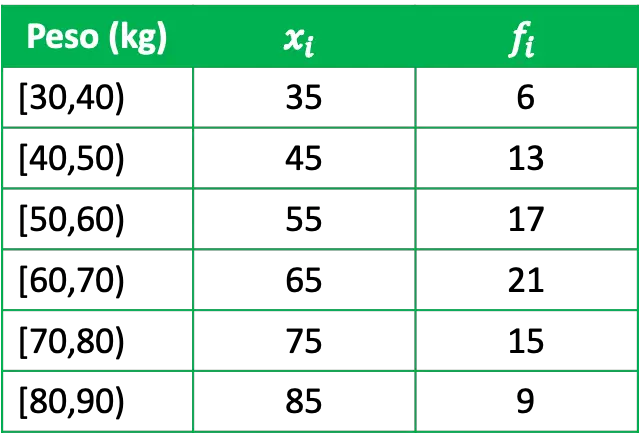
जहां x _i प्रत्येक समूह का वर्ग स्कोर है और f _i इसकी पूर्ण आवृत्ति है, यानी इस अंतराल में वजन रखने वाले लोगों की संख्या है।

अंकगणितीय माध्य निर्धारित करने के लिए, आवृत्ति तालिका में एक कॉलम जोड़ना आवश्यक है जो कि उनकी संबंधित निरपेक्ष आवृत्तियों द्वारा वर्ग नोट्स का उत्पाद है:

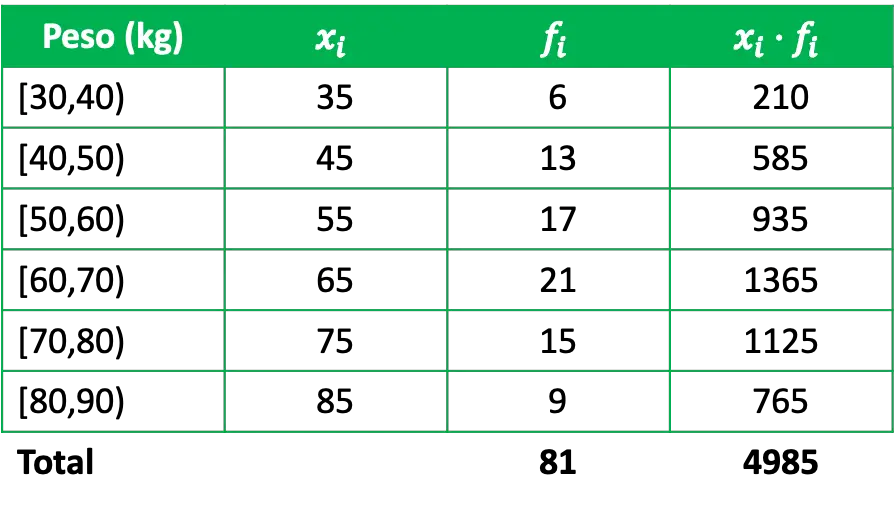
समूहीकृत डेटा के लिए हल किया गया अंकगणितीय माध्य अभ्यास

इस प्रकार, समूहीकृत डेटा के अंकगणितीय माध्य की गणना करने के लिए, वर्ग नोट्स के उत्पादों के योग को उनकी आवृत्तियों द्वारा डेटा की कुल संख्या से विभाजित करें:

$\displaystyle\overline{x}=\frac{\sum_{i=1}^N x_i\cdot f_i}{\sum_{i=1}^N f_i} =\frac{4985}{81}=61,54 \text{ kg}$

अंकगणित माध्य के गुण

अंकगणितीय औसत की निम्नलिखित विशेषताएं हैं:

किसी वितरण में माध्य से सभी डेटा के विचलन का योग शून्य होता है।

$\sum_{i=1}^N\left(x_i-\overline{x}\right)=0$

यदि हम किसी नमूने में सभी डेटा में समान मात्रा जोड़ते हैं, तो नमूना का मतलब उस मात्रा से बढ़ जाता है।

गुणन के साथ भी यही बात होती है, यदि कोई किसी नमूने के सभी मानों को किसी संख्या से गुणा करता है, तो नमूना माध्य उस संख्या से गुणा हो जाता है।

अंकगणितीय माध्य की गणना केवल मात्रात्मक चर में की जा सकती है। दूसरे शब्दों में, आप गुणात्मक चरों का औसत नहीं ले सकते।

अंकगणितीय माध्य हमेशा वितरण के न्यूनतम और अधिकतम के बीच का मान होगा।

$\text{min}\{x_1,x_2,...,x_N\}\leq \cfrac{x_1+\dots +x_N}{N}\leq \text{max}\{x_1,x_2,...,x_N\}$

इस प्रकार का औसत बहुत अधिक या बहुत कम मूल्यों के प्रति बहुत संवेदनशील होता है, जिससे अंकगणितीय औसत के परिणाम में महत्वपूर्ण परिवर्तन हो सकता है।

किसी डेटा सेट का अंकगणितीय माध्य हमेशा उसी डेटा सेट के ज्यामितीय माध्य के बराबर या उससे अधिक होता है।

$\displaystyle\frac{x_1+x_2+\dots+x_N}{N}\geq \sqrt[N]{x_1+x_2+\dots+x_N}$

एक्सेल के साथ अंकगणितीय माध्य की गणना करें

एक्सेल में अंकगणितीय औसत की गणना करना बहुत सरल है, क्योंकि आपको बस एक शीट पर डेटा दर्ज करना है और औसत फ़ंक्शन का उपयोग करना है।

उदाहरण के लिए, हमारे द्वारा समझाए गए पहले हल किए गए अभ्यास से डेटा का अंकगणितीय औसत निर्धारित करने के लिए, बस सभी डेटा को एक एक्सेल दस्तावेज़ में कॉपी करें और एक सेल में निम्नलिखित सूत्र लिखें: =AVERAGE(9;7;5; 8;7) ,5) . फ़ंक्शन डेटा का अंकगणितीय माध्य लौटाएगा, जो 7.3 है।

जाहिर है, एक्सेल प्रोग्राम के साथ कुछ संख्याओं के अंकगणितीय माध्य को हाथ से गणना करने की तुलना में बहुत तेज़ है, खासकर जब नमूना आकार बहुत बड़ा होता है।

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने