अनुपात के लिए परिकल्पना परीक्षण

द्वारा डॉ. बेंजामिन एंडरसन अगस्त 3, 2023 आंकड़े शून्य टिप्पणियां

यह आलेख बताता है कि आंकड़ों में परिकल्पना परीक्षण का क्या अनुपात है। इसलिए आपको अनुपात के लिए परिकल्पना परीक्षण का सूत्र मिलेगा और इसके अलावा, यह कैसे किया जाता है इसे पूरी तरह से समझने के लिए एक चरण-दर-चरण अभ्यास भी मिलेगा।

अनुपात के लिए परिकल्पना परीक्षण क्या है?

अनुपात परिकल्पना परीक्षण एक सांख्यिकीय पद्धति है जिसका उपयोग यह निर्धारित करने के लिए किया जाता है कि जनसंख्या अनुपात की शून्य परिकल्पना को अस्वीकार किया जाए या नहीं।

इसलिए, अनुपात और महत्व के स्तर के लिए परिकल्पना परीक्षण आंकड़ों के मूल्य के आधार पर, शून्य परिकल्पना को अस्वीकार या स्वीकार कर लिया जाता है।

ध्यान दें कि परिकल्पना परीक्षण को परिकल्पना विरोधाभास, परिकल्पना परीक्षण या महत्व परीक्षण भी कहा जा सकता है।

अनुपात के लिए परिकल्पना परीक्षण सूत्र

अनुपात के लिए परिकल्पना परीक्षण आँकड़ा नमूना अनुपात में अंतर के अनुपात के मानक विचलन द्वारा विभाजित अनुपात के प्रस्तावित मूल्य के अंतर के बराबर है।

अनुपात के लिए परीक्षण परिकल्पना सूत्र इसलिए है:

$\displaystyle Z=\frac{\widehat{p}-p}{\displaystyle\sqrt{\frac{p(1-p)}{n}}}$

सोना:

$Z$

अनुपात के लिए परिकल्पना परीक्षण आँकड़ा है।
$\widehat{p}$

नमूना अनुपात है.
$p$

प्रस्तावित अनुपात का मान है.
$n$

नमूना आकार है.
$\displaystyle\sqrt{\frac{p(1-p)}{n}}$

अनुपात का मानक विचलन है.

ध्यान रखें कि अनुपात के लिए परिकल्पना परीक्षण आंकड़ों की गणना करना पर्याप्त नहीं है, बल्कि परिणाम की व्याख्या की जानी चाहिए:

यदि अनुपात के लिए परिकल्पना परीक्षण दोतरफा है, तो यदि सांख्यिकी का पूर्ण मान महत्वपूर्ण मान Z _α/2 से अधिक है, तो शून्य परिकल्पना खारिज कर दी जाती है।
यदि अनुपात के लिए परिकल्पना परीक्षण सही पूंछ से मेल खाता है, तो शून्य परिकल्पना खारिज कर दी जाती है यदि आँकड़ा महत्वपूर्ण मान Z _α से अधिक है।
यदि अनुपात के लिए परिकल्पना परीक्षण बाईं पूंछ से मेल खाता है, तो शून्य परिकल्पना खारिज कर दी जाती है यदि आँकड़ा महत्वपूर्ण मान -Z _α से कम है।

$\begin{array}{l}H_1: p\neq p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |Z|>Z_{\alpha/2} \text{ se rechaza } H_0\\[3ex]H_1: p> p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z>Z_{\alpha} \text{ se rechaza } H_0\\[3ex]H_1: p< p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z<-Z_{\alpha} \text{ se rechaza } H_0\end{array}$

याद रखें कि सामान्य वितरण तालिका से महत्वपूर्ण मान आसानी से प्राप्त किए जा सकते हैं।

➤ देखें: सामान्य वितरण तालिका

अनुपात के लिए परिकल्पना परीक्षण का उदाहरण

एक बार जब हम अनुपात के लिए परिकल्पना परीक्षण की परिभाषा देखते हैं और इसका सूत्र क्या है, तो हम अवधारणा को बेहतर ढंग से समझने के लिए एक उदाहरण हल करेंगे।

इसके निर्माता के अनुसार, किसी विशिष्ट बीमारी के खिलाफ कोई दवा 70% प्रभावी होती है। प्रयोगशाला में, हम इस दवा की प्रभावशीलता का परीक्षण करते हैं क्योंकि शोधकर्ताओं का मानना है कि अनुपात भिन्न है। इसके लिए 1,000 मरीजों के सैंपल पर दवा का परीक्षण किया जाता है और 641 लोग ठीक हो जाते हैं। शोधकर्ताओं की परिकल्पना को अस्वीकार करने या न करने के लिए 5% के महत्व स्तर के साथ जनसंख्या अनुपात पर एक परिकल्पना परीक्षण करें।

इस मामले में, जनसंख्या अनुपात के लिए परिकल्पना परीक्षण की शून्य परिकल्पना और वैकल्पिक परिकल्पना हैं:

$\begin{cases}H_0: p=0,70\\[2ex] H_1:p\neq 0,70 \end{cases}$

नमूने में दवा से ठीक हुए लोगों का अनुपात है:

$\widehat{p}=\cfrac{641}{1000}=0,641$

हम ऊपर देखे गए सूत्र को लागू करके अनुपात के लिए परिकल्पना परीक्षण आंकड़ों की गणना करते हैं:

$\begin{aligned} \displaystyle Z&=\frac{\widehat{p}-p}{\displaystyle\sqrt{\frac{p(1-p)}{n}}}\\[2ex]Z&=\frac{0,641-0,70}{\displaystyle\sqrt{\frac{0,70\cdot (1-0,70)}{1000}}} \\[2ex] Z&=-4,07\end{aligned}}$

दूसरी ओर, चूँकि महत्व स्तर 0.05 है और यह दो-पुच्छ परिकल्पना परीक्षण है, परीक्षण का महत्वपूर्ण मान 1.96 है।

$Z_{0,025}=1,96$

➤ देखें: महत्व स्तर 0.05

निष्कर्ष में, परीक्षण आँकड़ों का पूर्ण मूल्य महत्वपूर्ण मूल्य से अधिक है, इसलिए हम शून्य परिकल्पना को अस्वीकार करते हैं और वैकल्पिक परिकल्पना को स्वीकार करते हैं।

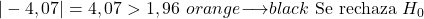$|-4,07|=4,07>1,96 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Se rechaza } H_0″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”424″ style=”vertical-align: -5px;”></p> </p> <div style=$ ➤ देखें: माध्य के लिए परिकल्पना परीक्षण

दो नमूना अनुपातों के लिए परिकल्पना परीक्षण

दो नमूनों के अनुपात के लिए परिकल्पना परीक्षण का उपयोग उस शून्य परिकल्पना को अस्वीकार या स्वीकार करने के लिए किया जाता है कि दो अलग-अलग आबादी के अनुपात बराबर हैं।

इस प्रकार, दो-नमूना अनुपात के लिए एक परिकल्पना परीक्षण की शून्य परिकल्पना हमेशा होती है:

$H_0: p_1=p_2$

जबकि वैकल्पिक परिकल्पना तीन विकल्पों में से एक हो सकती है:

 *** QuickLaTeX cannot compile formula:
\begin{array}{l}H_1:p_1\neq p_2\\[2ex]H_1:p_1>p_2\\[2ex]H_1:p_1 The combined ratio of the two samples is calculated as follows:[latex]p=\cfrac {x_1+x_2}{n_1+n_2}

*** Error message:
Missing $ inserted.
leading text: \begin{array}{l}
Please use \mathaccent for accents in math mode.
leading text: ...H_1:p_1>p_2\\[2ex]H_1:p_1 The combined ratio
Please use \mathaccent for accents in math mode.
leading text: ...\[2ex]H_1:p_1 The combined ratio of the two
Please use \mathaccent for accents in math mode.
leading text: ...combined of the two samples is calculated
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.

और दो नमूना अनुपातों के लिए परिकल्पना परीक्षण आंकड़ों की गणना करने का सूत्र है:

$\displaystyle Z=\frac{\displaystyle \frac{x_1}{n_1}-\frac{x_2}{n_2}}{\displaystyle \sqrt{p(1-p)\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}}$

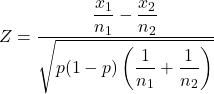
सोना:

$Z$

दो-नमूना अनुपातों के लिए परिकल्पना परीक्षण आँकड़ा है।
$x_1$

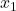
नमूना 1 में परिणामों की संख्या है.
$x_2$

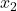
नमूना 2 में परिणामों की संख्या है।
$n_1$

नमूना आकार 1 है.
$n_2$

नमूना आकार 2 है.
$p$

दो नमूनों का संयुक्त अनुपात है.

K नमूना अनुपात के लिए परिकल्पना परीक्षण

K नमूनों के अनुपात के बारे में एक परिकल्पना परीक्षण में, लक्ष्य यह निर्धारित करना है कि क्या विभिन्न आबादी के सभी अनुपात समान हैं या, इसके विपरीत, क्या अलग-अलग अनुपात हैं। इसलिए, इस मामले में शून्य परिकल्पना और वैकल्पिक परिकल्पना हैं:

$\begin{cases}H_0: \text{Todas las proporciones son iguales}\\[2ex] H_1: \text{No todas las proporciones son iguales} \end{cases}$

इस मामले में, सभी नमूनों के संयुक्त अनुपात की गणना निम्नानुसार की जाती है:

$p=\cfrac{\displaystyle\sum_{i=1}^k x_i}{\displaystyle\sum_{i=1}^k n_i}=\cfrac{x_1+x_2+\dots+x_k}{n_1+n_2+\dots+n_k}$

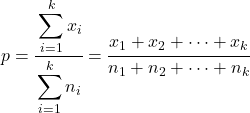
K नमूना अनुपात के लिए परिकल्पना परीक्षण आँकड़ा खोजने का सूत्र है:

$\displaystyle \chi^2 =\sum_{i=1}^k \frac{(x_i-e_i)^2}{e_i}$

$\displaystyle\chi^2 = \frac{(x_1-e_1)^2}{e_1} +\frac{(x_2-e_2)^2}{e_2} +\dots+\frac{(x_k-e_k)^2}{e_k}$

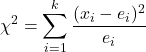
सोना:

$\chi^2$

k नमूना अनुपात के लिए परिकल्पना परीक्षण आँकड़ा है। इस मामले में, आँकड़ा ची-स्क्वायर वितरण का अनुसरण करता है।
$x_i$

नमूना i में परिणामों की संख्या है।
$n_i$

नमूना आकार है I
$p$

सभी नमूनों का संयुक्त अनुपात है।
$e_i$

नमूना i से अपेक्षित हिट की संख्या है। इसकी गणना संयुक्त अनुपात को गुणा करके की जाती है

$p$

नमूना आकार के अनुसार

$n_i$

.

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

नमस्ते, मैं बेंजामिन हूं, एक सेवानिवृत्त सांख्यिकी प्रोफेसर जो अब समर्पित Statorials शिक्षक बन गया है। सांख्यिकी के क्षेत्र में व्यापक अनुभव और विशेषज्ञता के साथ, मैं Statorials के माध्यम से छात्रों को सशक्त बनाने के लिए अपना ज्ञान साझा करने के लिए उत्सुक हूं। अधिक जाने

अनुपात के लिए परिकल्पना परीक्षण क्या है?

अनुपात के लिए परिकल्पना परीक्षण सूत्र

अनुपात के लिए परिकल्पना परीक्षण का उदाहरण

दो नमूना अनुपातों के लिए परिकल्पना परीक्षण

K नमूना अनुपात के लिए परिकल्पना परीक्षण

लेखक के बारे में

डॉ. बेंजामिन एंडरसन

एक टिप्पणी जोड़ने