आउटलेर्स के साथ बॉक्स प्लॉट कैसे पढ़ें (उदाहरण के साथ)

बॉक्स प्लॉट एक प्रकार का प्लॉट है जो डेटा सेट का पांच अंकों का सारांश प्रदर्शित करता है, जिसमें शामिल हैं:

• न्यूनतम मूल्य
• प्रथम चतुर्थक (25वाँ प्रतिशतक)
• माध्यिका मान
• तीसरा चतुर्थक (75वाँ प्रतिशतक)
• अधिकतम मूल्य

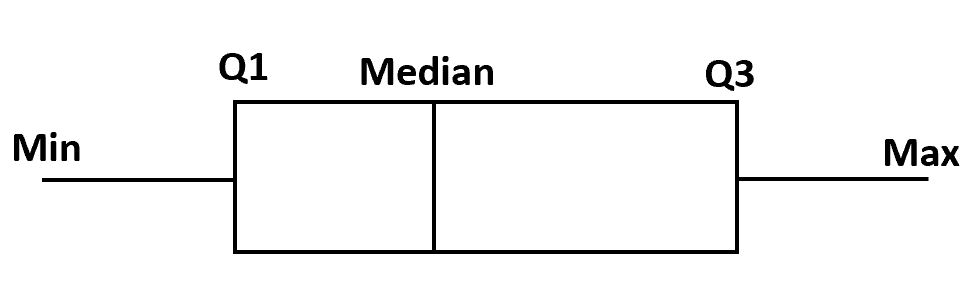
एक बॉक्स प्लॉट बनाने के लिए, हम पहले पहले से तीसरे चतुर्थक तक एक बॉक्स बनाते हैं।

इसके बाद, हम मध्यिका पर एक ऊर्ध्वाधर रेखा खींचते हैं।

अंत में, हम न्यूनतम और अधिकतम मान तक चतुर्थक की “मूंछें” खींचते हैं।

अधिकांश सांख्यिकीय सॉफ़्टवेयर में, एक अवलोकन को एक बाहरी के रूप में परिभाषित किया जाता है यदि यह निम्नलिखित दो आवश्यकताओं में से एक को पूरा करता है:

• अवलोकन प्रथम चतुर्थक (Q1) के नीचे अंतरचतुर्थक सीमा का 1.5 गुना है
• अवलोकन तीसरे चतुर्थक (Q3) के ऊपर अंतरचतुर्थक सीमा का 1.5 गुना है।

यदि डेटा सेट में कोई आउटलेयर मौजूद है, तो इसे आमतौर पर बॉक्स प्लॉट में व्हिस्कर रेंज के बाहर एक छोटे बिंदु के साथ लेबल किया जाता है:

जब ऐसा होता है, तो बॉक्सप्लॉट में “न्यूनतम” और “अधिकतम” मान क्रमशः Q1 – 1.5*IQR और Q3 + 1.5*IQR के मान निर्दिष्ट किए जाते हैं।

निम्नलिखित उदाहरण दिखाता है कि आउटलेर्स के साथ और उसके बिना बॉक्स प्लॉट की व्याख्या कैसे करें।

उदाहरण: आउटलेर्स के साथ एक बॉक्स प्लॉट की व्याख्या करना

मान लीजिए कि हम दो अलग-अलग टीमों के बास्केटबॉल खिलाड़ियों द्वारा बनाए गए अंकों के वितरण की कल्पना करने के लिए निम्नलिखित दो बॉक्स प्लॉट बनाते हैं:

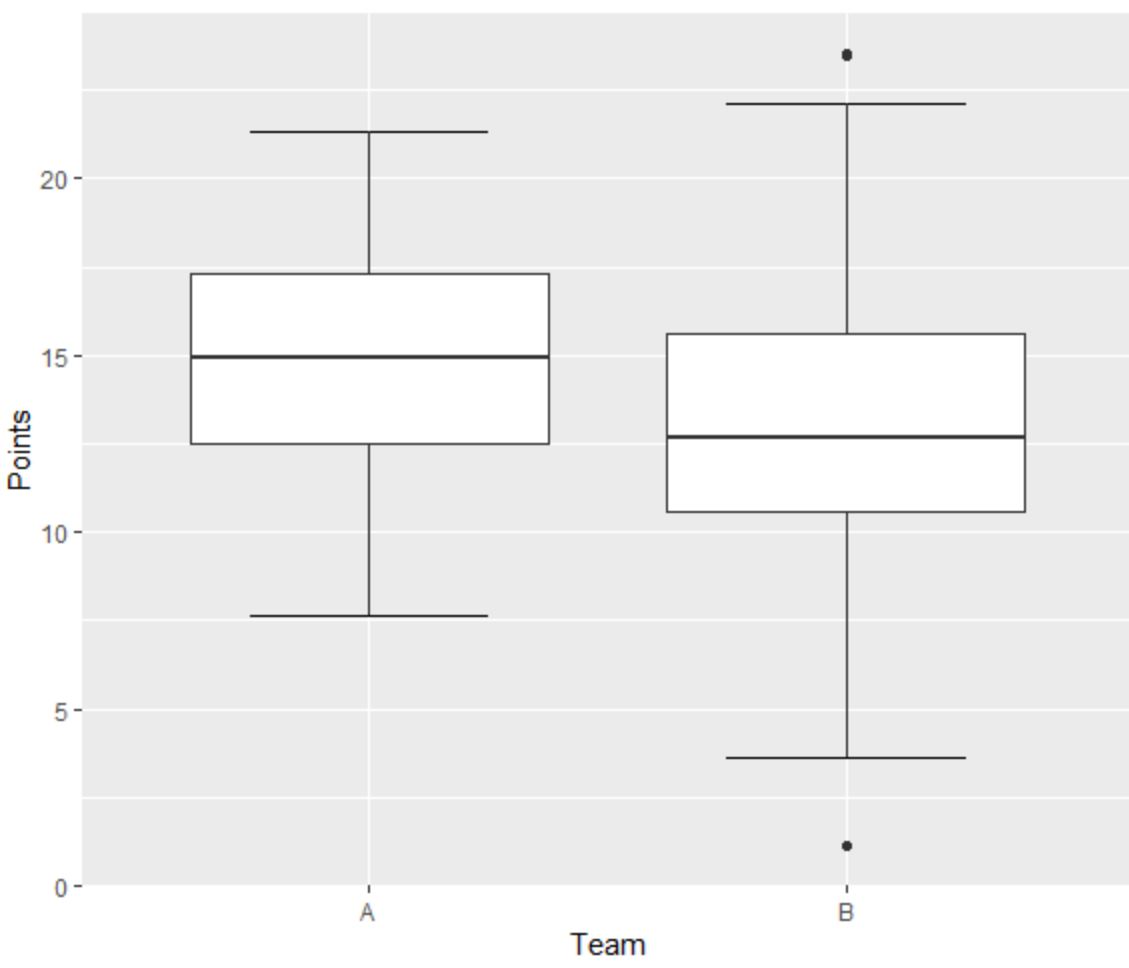
टीम ए के लिए बाएँ बॉक्सप्लॉट में कोई आउटलेयर नहीं है क्योंकि न्यूनतम या अधिकतम मूंछ के बाहर कोई छोटे बिंदु स्थित नहीं हैं।

हालाँकि, टीम बी के लिए सही बॉक्सप्लॉट में “अधिकतम” मान के ऊपर एक आउटलायर और “न्यूनतम” मान के नीचे एक आउटलायर है।

टीम बी के लिए “अंक” चर के वितरण के लिए वर्तमान पांच अंकों का सारांश यहां दिया गया है:

• न्यूनतम मान: 1.1
• प्रथम चतुर्थक: 10.5
• माध्यिका: 12.7
• तृतीय चतुर्थक: 15.6
• अधिकतम मान: 23.5

यहां बताया गया है कि संभावित आउटलेर्स की सीमा की गणना कैसे करें:

अंतरचतुर्थक पैमाना : तृतीय चतुर्थक – प्रथम चतुर्थक = 15.6 – 10.5 = 5.1

निचली सीमा : Q1 – 1.5*IQR = 10.5 – 1.5*5.1 = 2.85

ऊपरी सीमा : Q3 + 1.5*IQR = 15.6 + 1.5*5.1 = 23.25

बॉक्सप्लॉट में न्यूनतम और अधिकतम मानों के लिए मूंछें 2.85 और 23.25 पर रखी गई हैं।

इस प्रकार, 1.1 और 23.5 के मान वाले अवलोकन दोनों बॉक्सप्लॉट में आउटलेयर के रूप में योग्य हैं क्योंकि वे निचली और ऊपरी सीमा से बाहर आते हैं।

बोनस : यहां वह सटीक कोड है जिसका उपयोग हमने आर प्रोग्रामिंग भाषा में इन दो बॉक्सप्लॉट को बनाने के लिए किया था:

 library (ggplot2)

#make this example reproducible 
set. seeds (2)

#create data frame
df <- data. frame (Team = factor(rep(c("A", "B"), each = 200)), 
                 Points = c(rnorm(200, mean = 15, sd = 3), 
                           rnorm(200, mean = 12, sd = 4))) 

#create box plots
ggplot(df, aes(x = Team, y = Points)) +
  stat_boxplot(geom = " errorbar ", width = 0.5) +  
  geom_boxplot() 

#calculate summary statistics for each team
tapply(df$Points, df$Team, summary)

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल बॉक्स प्लॉट्स के बारे में अतिरिक्त जानकारी प्रदान करते हैं:

बॉक्स प्लॉट्स की तुलना कैसे करें
बॉक्स प्लॉट्स में विषमता की पहचान कैसे करें
बॉक्सप्लॉट की अंतरचतुर्थक सीमा कैसे ज्ञात करें