आर में केंद्रीय सीमा प्रमेय कैसे लागू करें (उदाहरण के साथ)

केंद्रीय सीमा प्रमेय में कहा गया है कि यदि नमूना आकार काफी बड़ा है, तो नमूना माध्य का नमूना वितरण लगभग सामान्य है, भले ही जनसंख्या वितरण सामान्य न हो।

केंद्रीय सीमा प्रमेय यह भी बताता है कि नमूना वितरण में निम्नलिखित गुण होंगे:

1. नमूना वितरण का माध्य जनसंख्या वितरण के माध्य के बराबर होगा:

एक्स = µ

2. नमूना वितरण का मानक विचलन नमूना आकार से विभाजित जनसंख्या वितरण के मानक विचलन के बराबर होगा:

एस = σ /एन

निम्नलिखित उदाहरण दिखाता है कि आर में केंद्रीय सीमा प्रमेय को कैसे लागू किया जाए।

उदाहरण: आर में केंद्रीय सीमा प्रमेय का अनुप्रयोग

मान लीजिए कि कछुए के खोल की चौड़ाई एकसमान वितरण का पालन करती है जिसमें न्यूनतम चौड़ाई 2 इंच और अधिकतम चौड़ाई 6 इंच होती है।

यानी, अगर हम यादृच्छिक रूप से एक कछुए का चयन करते हैं और उसके खोल की चौड़ाई मापते हैं, तो इसकी चौड़ाई भी 2 से 6 इंच के बीच होने की संभावना है।

निम्नलिखित कोड दिखाता है कि आर में एक डेटासेट कैसे बनाया जाए जिसमें 1,000 कछुओं की कवच की चौड़ाई की माप हो, जो 2 और 6 इंच के बीच समान रूप से वितरित हो:

 #make this example reproducible
set. seeds (0)

#create random variable with sample size of 1000 that is uniformly distributed
data <- runif(n=1000, min=2, max=6)

#create histogram to visualize distribution of turtle shell widths
hist(data, col=' steelblue ', main=' Histogram of Turtle Shell Widths ')

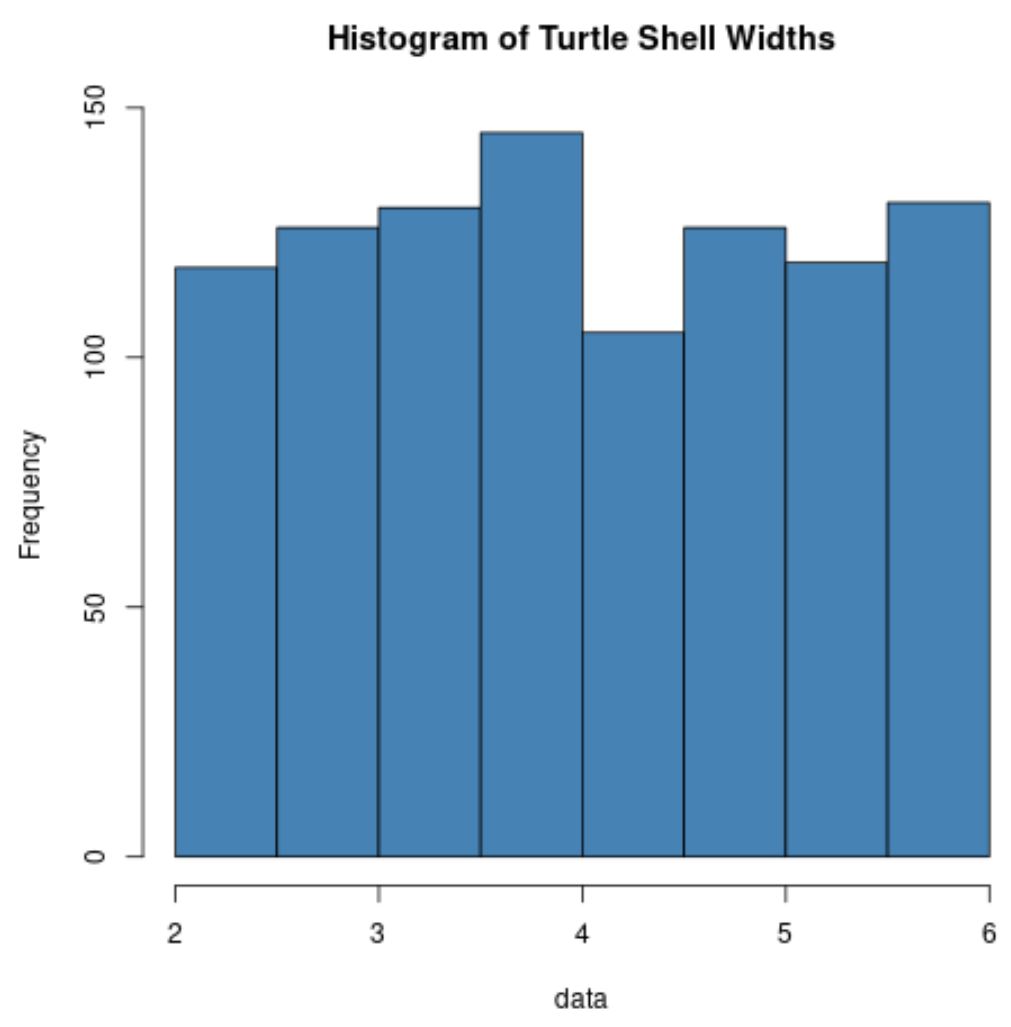
ध्यान दें कि कछुए के खोल की चौड़ाई का वितरण सामान्यतः बिल्कुल भी वितरित नहीं होता है।

अब कल्पना करें कि हम इस आबादी से 5 कछुओं के बार-बार यादृच्छिक नमूने लेते हैं और नमूना माध्य को बार-बार मापते हैं।

निम्नलिखित कोड दिखाता है कि इस प्रक्रिया को आर में कैसे करें और नमूना साधनों के वितरण की कल्पना करने के लिए एक हिस्टोग्राम बनाएं:

 #create empty vector to hold sample means
sample5 <- c()

#take 1,000 random samples of size n=5
n = 1000
for (i in 1:n){
sample5[i] = mean(sample(data, 5, replace= TRUE ))
}

#calculate mean and standard deviation of sample means
mean(sample5)

[1] 4.008103

sd(sample5)

[1] 0.5171083 

#create histogram to visualize sampling distribution of sample means
hist(sample5, col = ' steelblue ', xlab=' Turtle Shell Width ', main=' Sample size = 5 ') 

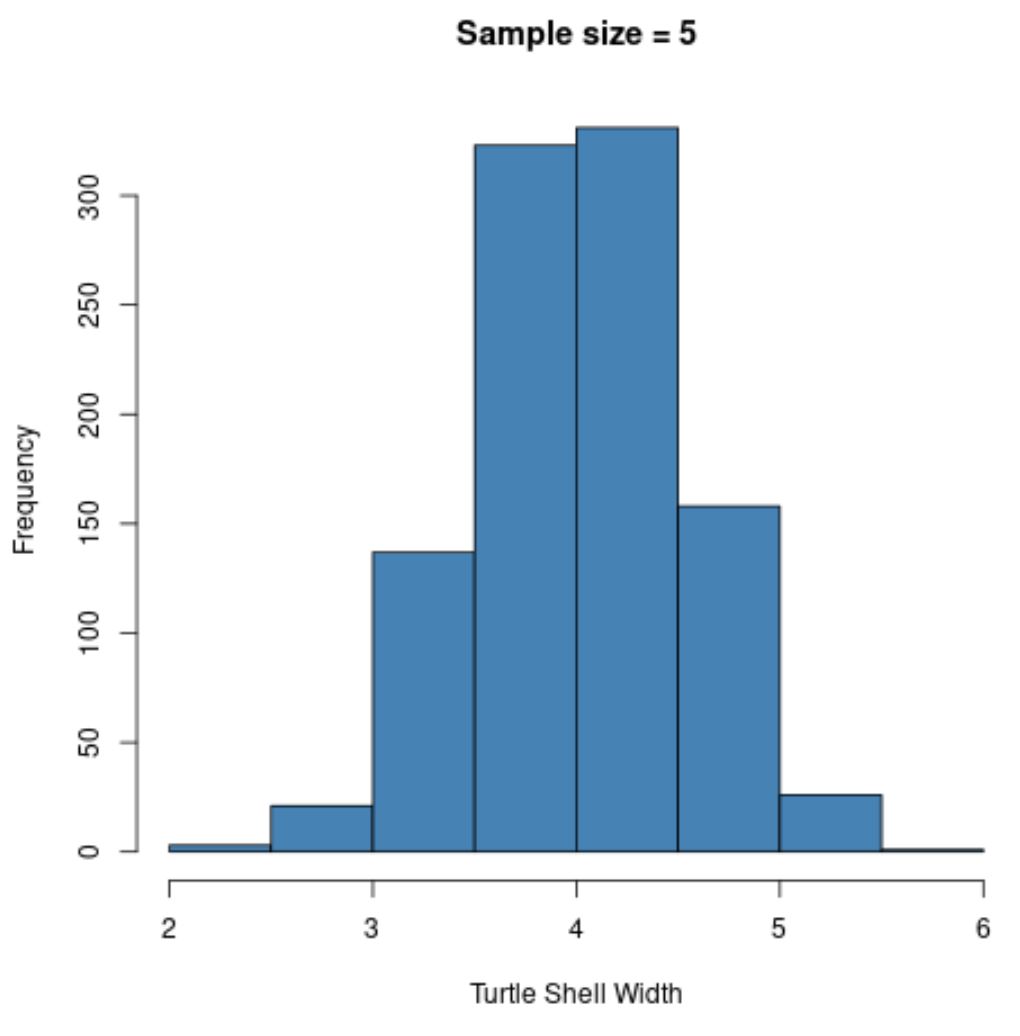
ध्यान दें कि नमूना साधनों का नमूना वितरण सामान्य रूप से वितरित प्रतीत होता है, भले ही जिस वितरण से नमूने आए थे वह सामान्य रूप से वितरित नहीं किया गया था।

इस नमूना वितरण के लिए नमूना माध्य और नमूना मानक विचलन पर भी ध्यान दें:

• x̄ : 4.008
• एस : 0.517

अब मान लीजिए कि हम अपने द्वारा उपयोग किए जाने वाले नमूना आकार को n=5 से n=30 तक बढ़ाते हैं और नमूने के हिस्टोग्राम को फिर से बनाते हैं:

 #create empty vector to hold sample means
sample30 <- c()

#take 1,000 random samples of size n=30
n = 1000
for (i in 1:n){
sample30[i] = mean(sample(data, 30, replace= TRUE ))
}

#calculate mean and standard deviation of sample means
mean(sample30)

[1] 4.000472

sd(sample30)

[1] 0.2003791

#create histogram to visualize sampling distribution of sample means
hist(sample30, col = ' steelblue ', xlab=' Turtle Shell Width ', main=' Sample size = 30 ') 

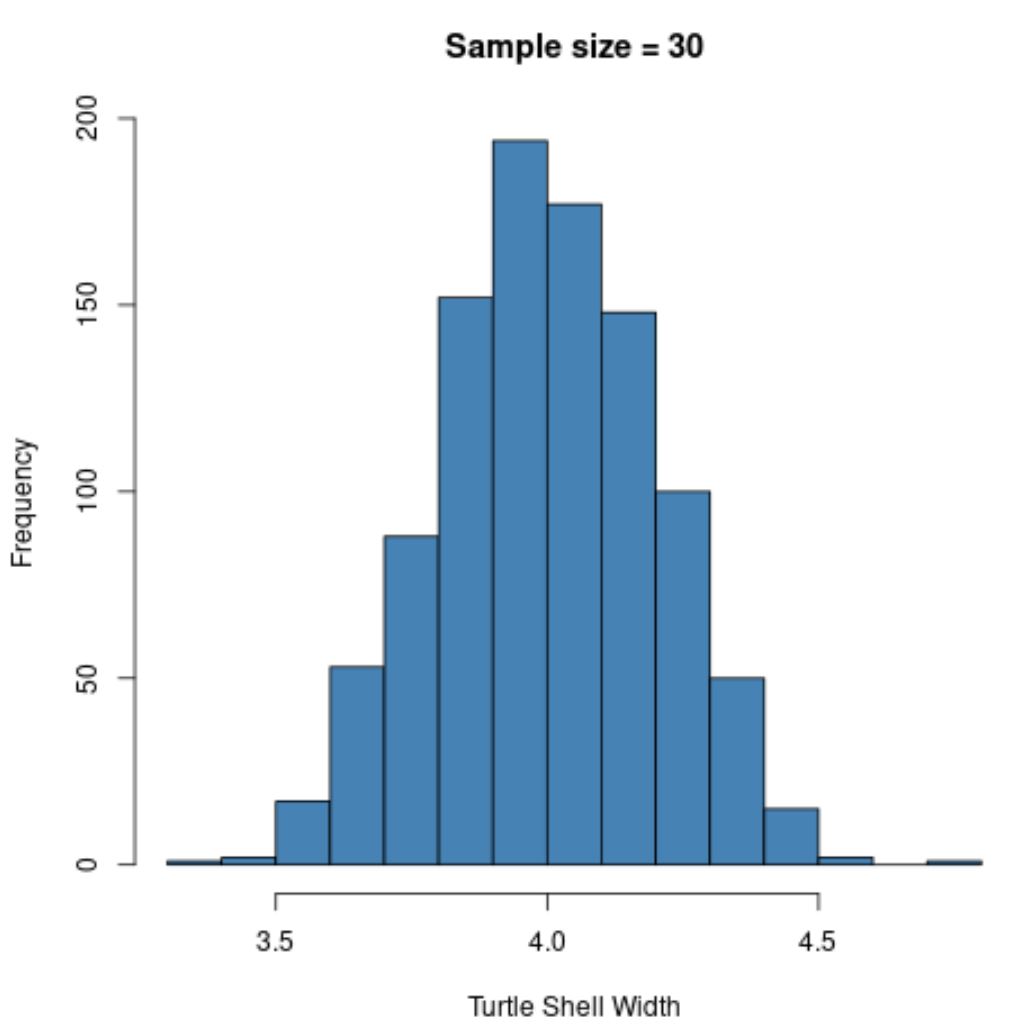
नमूना वितरण फिर से सामान्य रूप से वितरित किया जाता है, लेकिन नमूना मानक विचलन और भी छोटा है:

• एस : 0.200

ऐसा इसलिए है क्योंकि हमने पिछले उदाहरण (n=5) की तुलना में बड़े नमूना आकार (n=30) का उपयोग किया है, इसलिए नमूना साधनों का मानक विचलन और भी छोटा है।

यदि हम बड़े और बड़े नमूनों का उपयोग करना जारी रखते हैं, तो हम पाएंगे कि नमूना मानक विचलन छोटा और छोटा होता जाता है।

यह व्यवहार में केंद्रीय सीमा प्रमेय को दर्शाता है।

अतिरिक्त संसाधन

निम्नलिखित संसाधन केंद्रीय सीमा प्रमेय के बारे में अतिरिक्त जानकारी प्रदान करते हैं:

केंद्रीय सीमा प्रमेय का एक परिचय
केंद्रीय सीमा प्रमेय कैलकुलेटर
वास्तविक जीवन में केंद्रीय सीमा प्रमेय का उपयोग करने के 5 उदाहरण