आर में स्प्लाइन रिग्रेशन कैसे करें (उदाहरण के साथ)

स्पलाइन रिग्रेशन एक प्रकार का रिग्रेशन है जिसका उपयोग तब किया जाता है जब ऐसे बिंदु या “गांठें” होती हैं जहां डेटा में पैटर्न अचानक बदल जाता है और रैखिक रिग्रेशन और बहुपद रिग्रेशन डेटा को फिट करने के लिए पर्याप्त लचीले नहीं होते हैं।

निम्नलिखित चरण-दर-चरण उदाहरण दिखाता है कि आर में स्पलाइन रिग्रेशन कैसे करें।

चरण 1: डेटा बनाएं

सबसे पहले, आइए आर में दो वेरिएबल्स के साथ एक डेटासेट बनाएं और वेरिएबल्स के बीच संबंध को देखने के लिए एक स्कैटरप्लॉट बनाएं:

 #create data frame
df <- data. frame (x=1:20,
                 y=c(2, 4, 7, 9, 13, 15, 19, 16, 13, 10,
                     11, 14, 15, 15, 16, 15, 17, 19, 18, 20))

#view head of data frame
head(df)

  xy
1 1 2
2 2 4
3 3 7
4 4 9
5 5 13
6 6 15

#create scatterplot
plot(df$x, df$y, cex= 1.5 , pch= 19 )

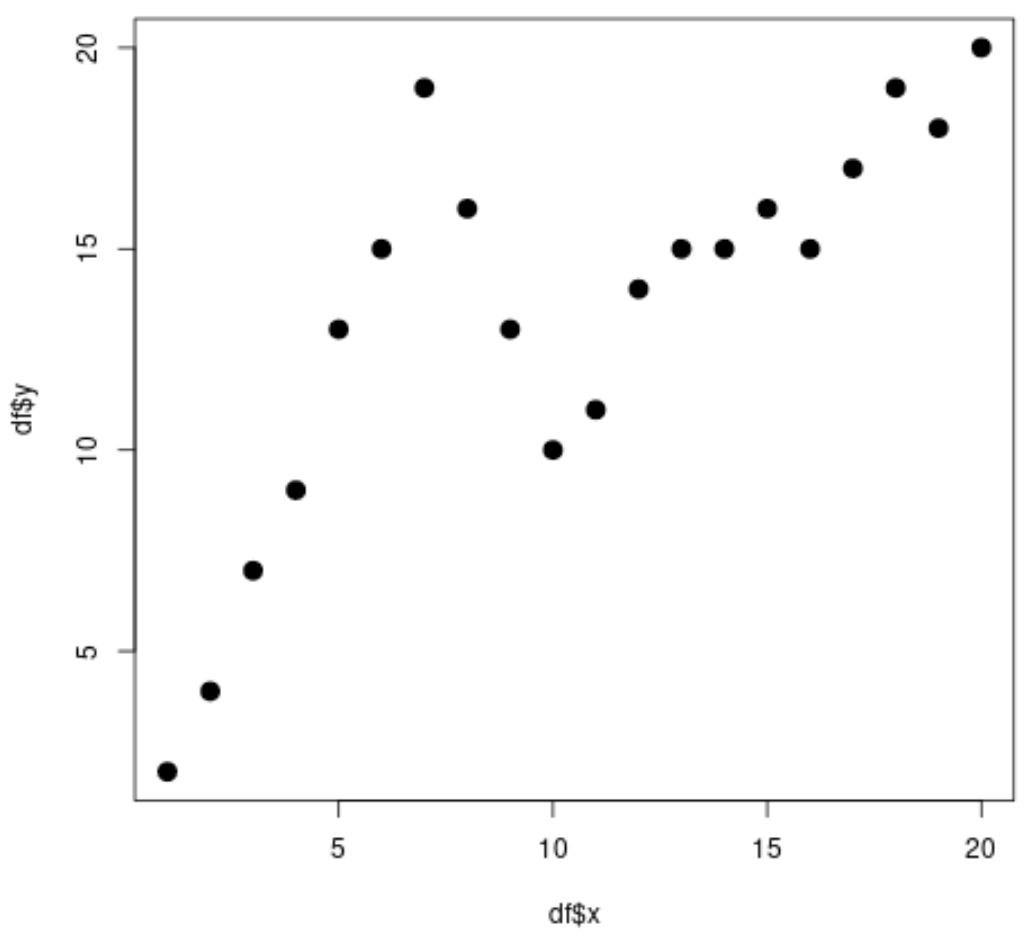
स्पष्ट रूप से x और y के बीच संबंध गैर-रैखिक है और वहां दो बिंदु या “नोड्स” प्रतीत होते हैं जहां डेटा में पैटर्न x=7 और x=10 पर अचानक बदल जाता है।

चरण 2: सरल रैखिक प्रतिगमन मॉडल फिट करें

आइए फिर इस डेटा सेट में एक सरल रैखिक प्रतिगमन मॉडल को फिट करने के लिए lm() फ़ंक्शन का उपयोग करें और स्कैटरप्लॉट पर प्रतिगमन रेखा को प्लॉट करें:

 #fit simple linear regression model
linear_fit <- lm(df$y ~ df$x)

#view model summary
summary(linear_fit)

Call:
lm(formula = df$y ~ df$x)

Residuals:
    Min 1Q Median 3Q Max 
-5.2143 -1.6327 -0.3534 0.6117 7.8789 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 6.5632 1.4643 4.482 0.000288 ***
df$x 0.6511 0.1222 5.327 4.6e-05 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.152 on 18 degrees of freedom
Multiple R-squared: 0.6118, Adjusted R-squared: 0.5903 
F-statistic: 28.37 on 1 and 18 DF, p-value: 4.603e-05

#create scatterplot
plot(df$x, df$y, cex= 1.5 , pch= 19 )

#add regression line to scatterplot
abline(linear_fit) 

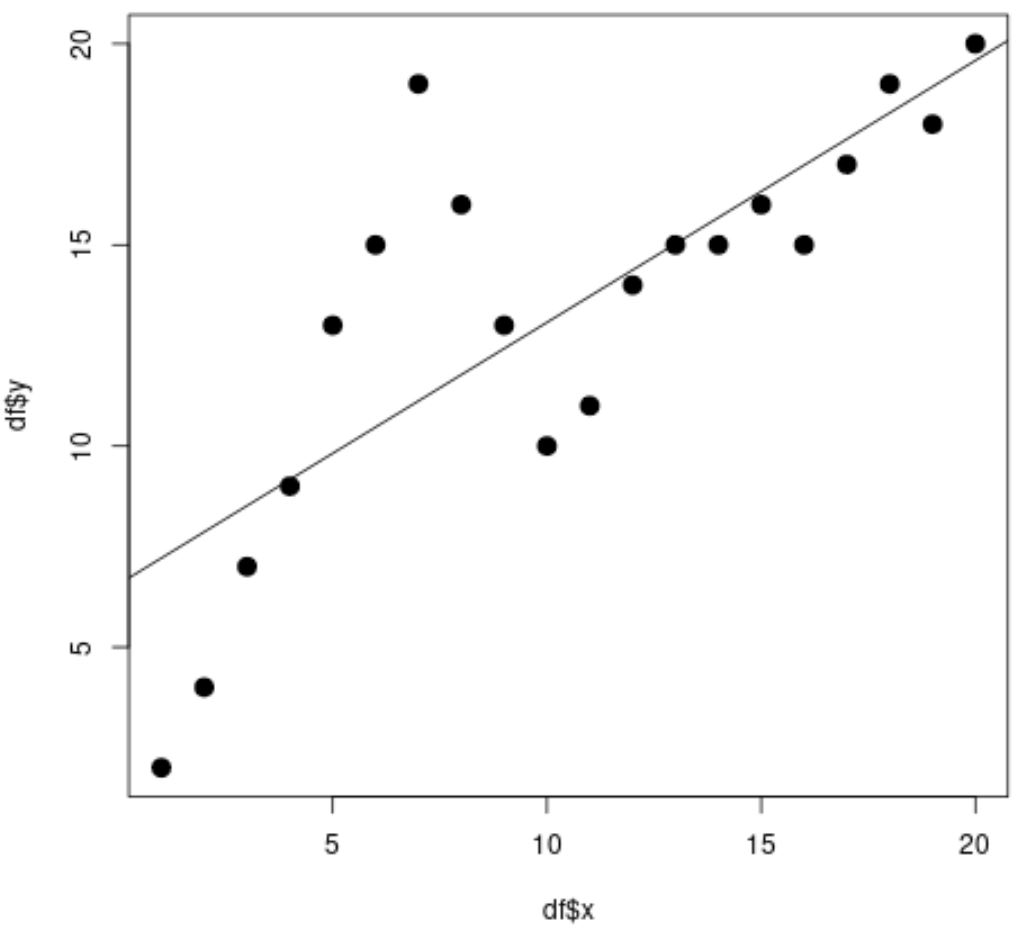
स्कैटरप्लॉट से, हम देख सकते हैं कि सरल रैखिक प्रतिगमन रेखा डेटा को अच्छी तरह से फिट नहीं करती है।

मॉडल परिणामों से, हम यह भी देख सकते हैं कि समायोजित आर-वर्ग मान 0.5903 है।

हम इसकी तुलना स्पलाइन मॉडल के समायोजित आर-वर्ग मान से करेंगे।

चरण 3: स्प्लाइन रिग्रेशन मॉडल को फिट करें

इसके बाद, आइए दो नोड्स के साथ एक स्पलाइन रिग्रेशन मॉडल को फिट करने के लिए स्प्लिन पैकेज से बीएस () फ़ंक्शन का उपयोग करें, और फिर स्कैटरप्लॉट पर फिट किए गए मॉडल को प्लॉट करें:

 library (splines)

#fit spline regression model
spline_fit <- lm(df$y ~ bs(df$x, knots=c( 7 , 10 )))

#view summary of spline regression model
summary(spline_fit)

Call:
lm(formula = df$y ~ bs(df$x, knots = c(7, 10)))

Residuals:
     Min 1Q Median 3Q Max 
-2.84883 -0.94928 0.08675 0.78069 2.61073 

Coefficients:
                            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 2.073 1.451 1.429 0.175    
bs(df$x, knots = c(7, 10))1 2.173 3.247 0.669 0.514    
bs(df$x, knots = c(7, 10))2 19.737 2.205 8.949 3.63e-07 ***
bs(df$x, knots = c(7, 10))3 3.256 2.861 1.138 0.274    
bs(df$x, knots = c(7, 10))4 19.157 2.690 7.121 5.16e-06 ***
bs(df$x, knots = c(7, 10))5 16.771 1.999 8.391 7.83e-07 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.568 on 14 degrees of freedom
Multiple R-squared: 0.9253, Adjusted R-squared: 0.8987 
F-statistic: 34.7 on 5 and 14 DF, p-value: 2.081e-07

#calculate predictions using spline regression model
x_lim <- range(df$x)
x_grid <- seq(x_lim[ 1 ], x_lim[ 2 ])
preds <- predict(spline_fit, newdata=list(x=x_grid))

#create scatter plot with spline regression predictions
plot(df$x, df$y, cex= 1.5 , pch= 19 )
lines(x_grid, preds) 

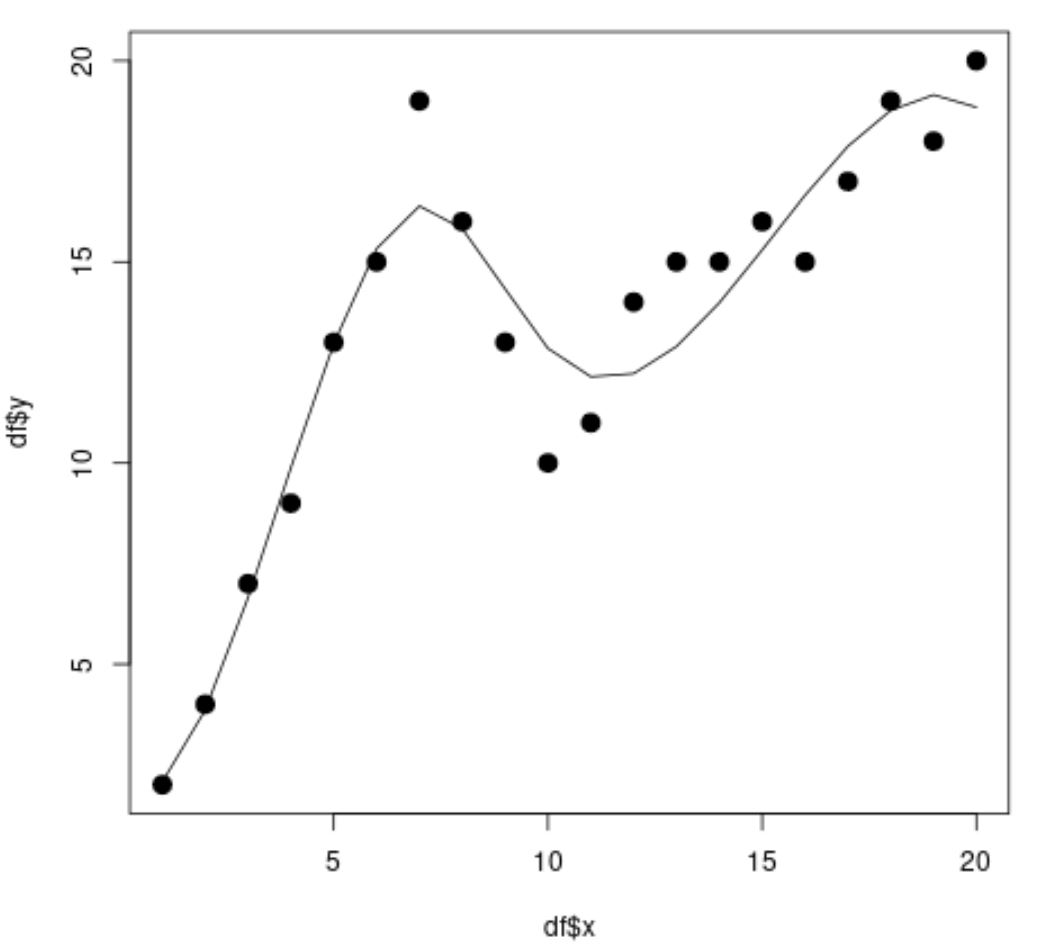
स्कैटरप्लॉट से, हम देख सकते हैं कि स्पलाइन रिग्रेशन मॉडल डेटा को काफी अच्छी तरह से फिट करने में सक्षम है।

मॉडल परिणामों से, हम यह भी देख सकते हैं कि समायोजित आर-वर्ग मान 0.8987 है।

इस मॉडल के लिए समायोजित आर-वर्ग मान सरल रैखिक प्रतिगमन मॉडल की तुलना में बहुत अधिक है, जो हमें बताता है कि स्पलाइन प्रतिगमन मॉडल डेटा को बेहतर ढंग से फिट करने में सक्षम है।

ध्यान दें कि इस उदाहरण के लिए हमने चुना है कि नोड्स x=7 और x=10 पर स्थित हैं।

व्यवहार में, आपको डेटा में पैटर्न कहां बदलते दिखाई देते हैं और आपकी डोमेन विशेषज्ञता के आधार पर स्वयं नोड स्थान चुनने की आवश्यकता होगी।

अतिरिक्त संसाधन

निम्नलिखित ट्यूटोरियल बताते हैं कि आर में अन्य सामान्य कार्य कैसे करें:

आर में मल्टीपल लीनियर रिग्रेशन कैसे करें
आर में घातीय प्रतिगमन कैसे करें
आर में भारित न्यूनतम वर्ग प्रतिगमन कैसे करें